Apa yang dimaksud dengan distribusi unimodal? (definisi & #038; contoh)
Distribusi unimodal adalah distribusi probabilitas yang mempunyai puncak yang jelas.
Hal ini berbeda dengan distribusi bimodal , yang memiliki dua puncak yang jelas:
Hal ini juga berbeda dengan distribusi multimodal , yang memiliki dua atau lebih puncak:
Catatan: Distribusi bimodal hanyalah jenis distribusi multimodal tertentu.
Contoh distribusi unimodal
Berikut beberapa contoh distribusi unimodal dalam praktiknya.
Contoh 1: Berat lahir bayi
Diketahui bahwa distribusi berat badan bayi baru lahir mengikuti distribusi unimodal dengan rata-rata sekitar 7,5 pon. Jika kita membuat histogram berat badan bayi, kita akan melihat “puncak” pada 7,5 pon, dengan beberapa bayi memiliki berat lebih banyak dan yang lainnya memiliki berat lebih sedikit.

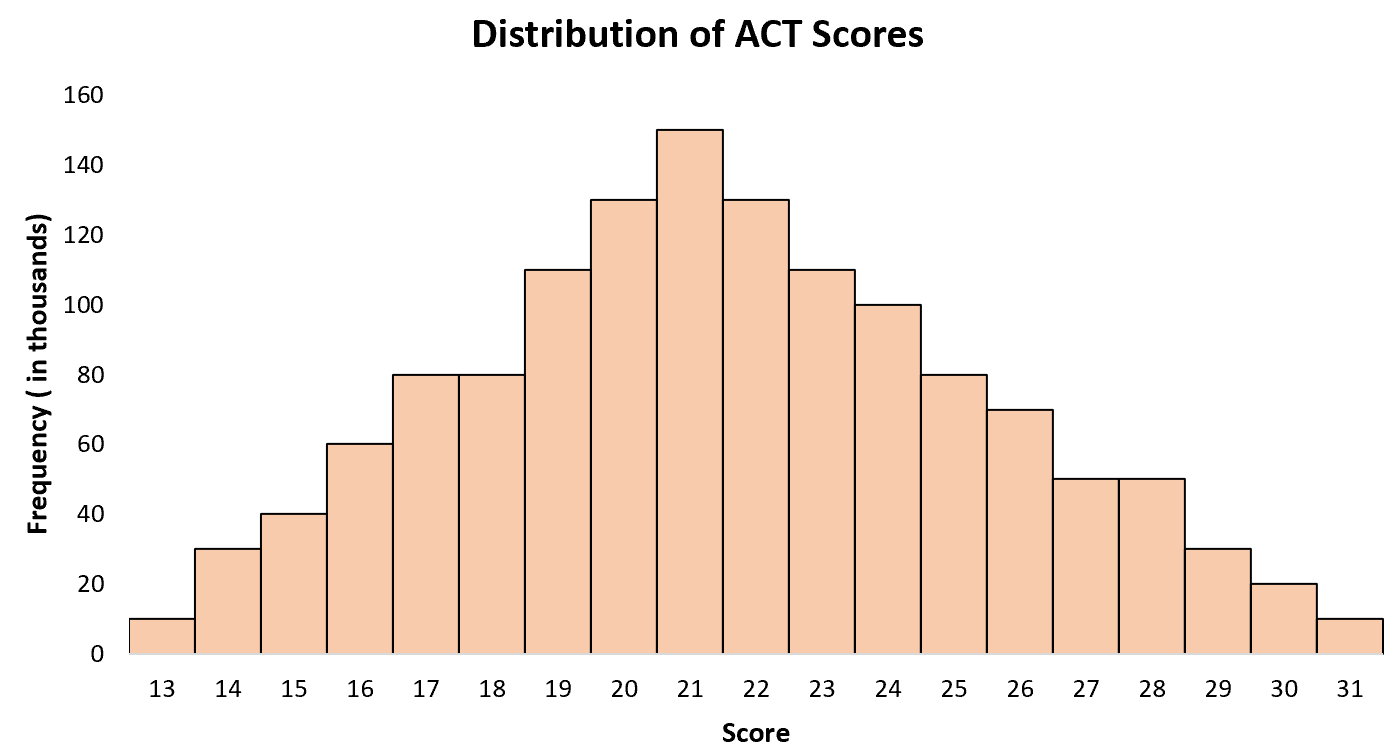
Contoh 2: Skor ACT
Nilai rata-rata ACT untuk siswa sekolah menengah atas di Amerika Serikat adalah sekitar 21, dengan beberapa siswa mendapat nilai lebih rendah dan ada yang mendapat nilai lebih tinggi. Jika kita membuat histogram skor ACT untuk semua siswa di Amerika Serikat, kita akan melihat satu “puncak” pada usia 21 tahun, dengan skor lebih tinggi untuk beberapa siswa dan skor lebih rendah untuk siswa lainnya.
Contoh 3: ukuran sepatu
Distribusi ukuran sepatu pria adalah distribusi unimodal dengan “puncak” sekitar 10. Jika kita membuat histogram semua ukuran sepatu pria, kita akan melihat satu puncak di angka 10 dengan beberapa pria mengenakan ukuran sepatu yang lebih besar dan yang lainnya mengenakan sepatu yang lebih besar. ukuran. ukuran lebih kecil.
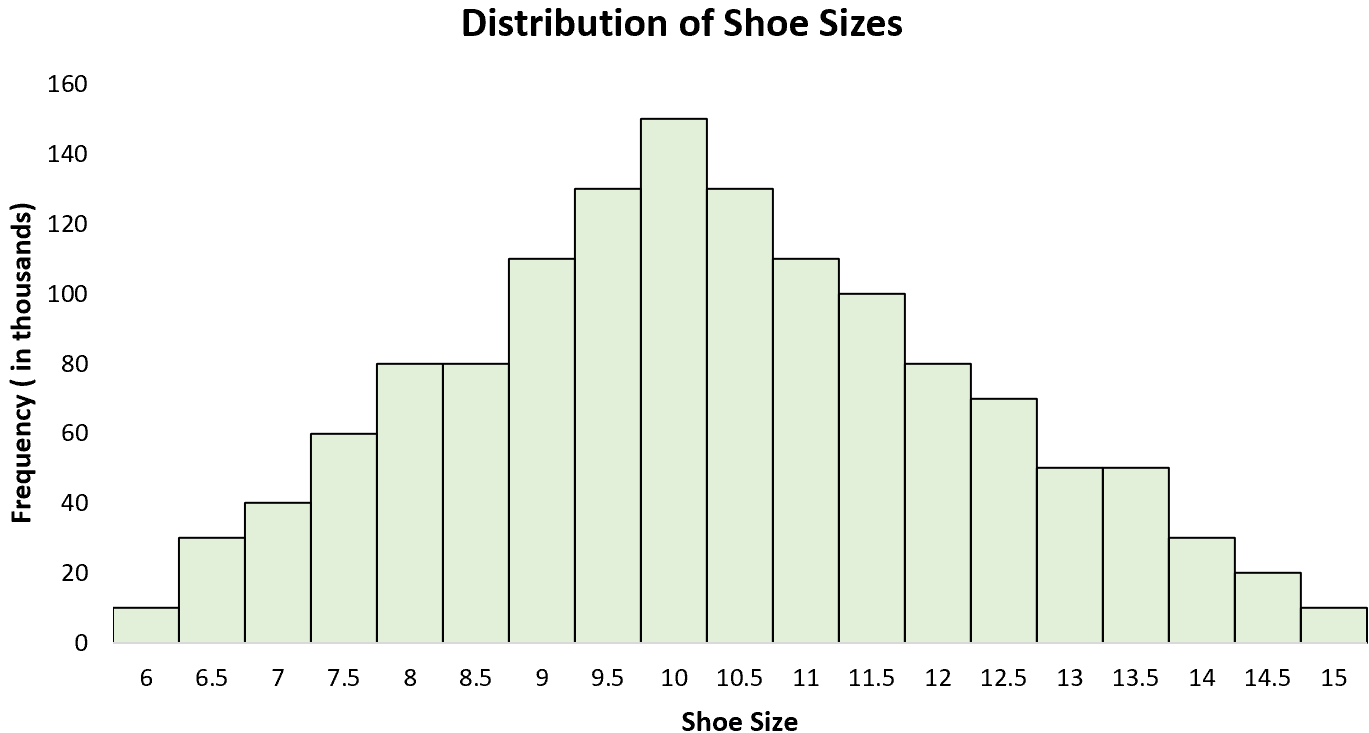
Distribusi unimodal dalam statistik
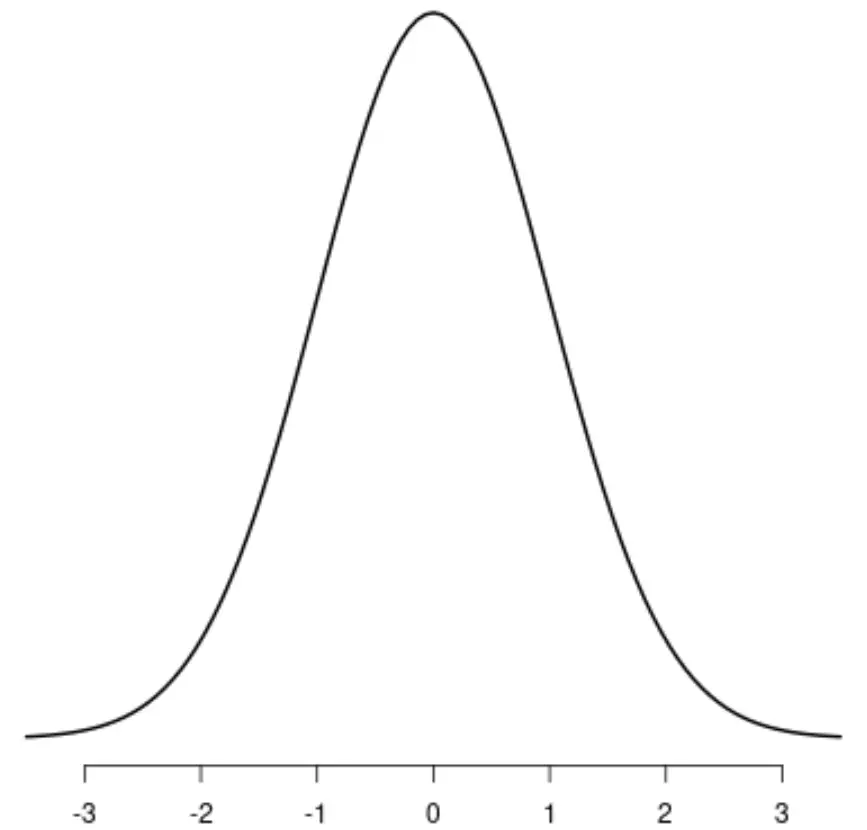
Distribusi probabilitas dalam statistik berikut semuanya merupakan distribusi unimodal:
Distribusi normal
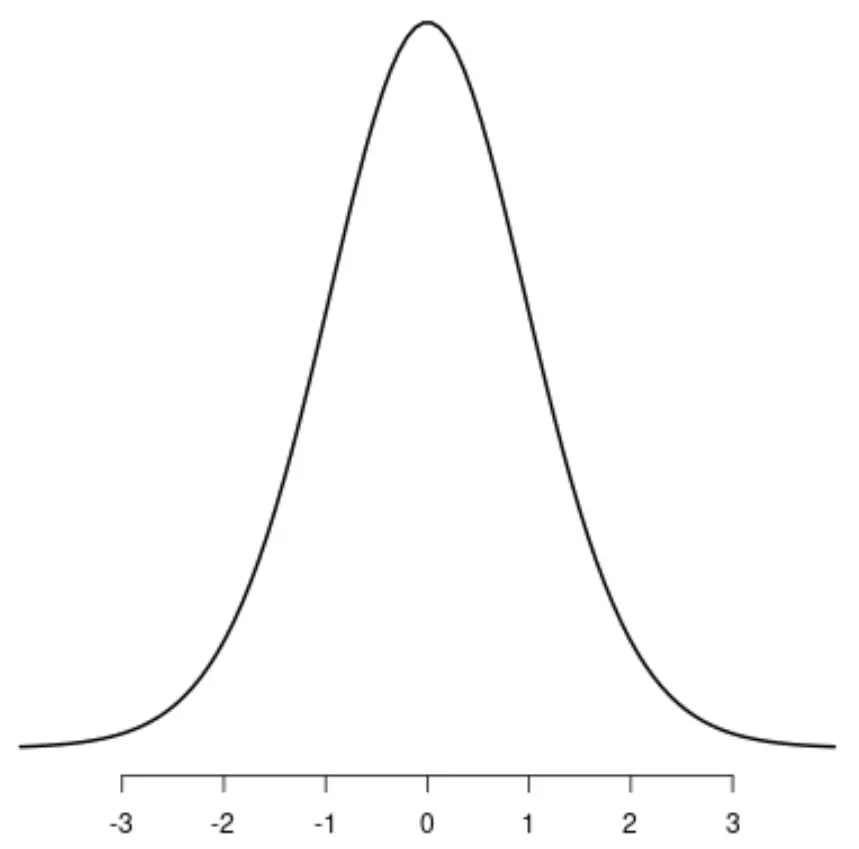
Distribusi t
Distribusi seragam

Distribusi Cauchy
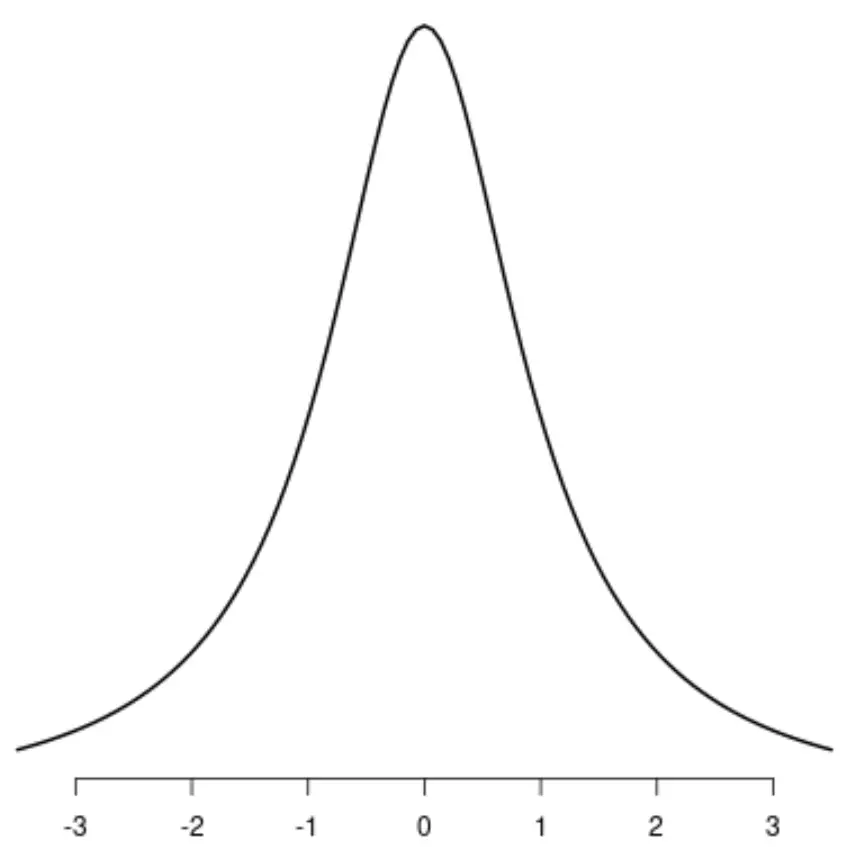
Perhatikan bahwa masing-masing distribusi ini mempunyai satu puncak yang berbeda.
Bagaimana menganalisis distribusi unimodal
Kita sering mendeskripsikan distribusi unimodal menggunakan tiga ukuran tendensi sentral yang berbeda :
- Rata-rata : Nilai rata-rata
- Median : Nilai median
- Mode : Nilai yang paling sering muncul
Tergantung pada asimetri distribusinya, ketiga pengukuran ini dapat ditemukan di tempat berbeda.
Distribusi miring ke kiri: Mean < Median < Mode
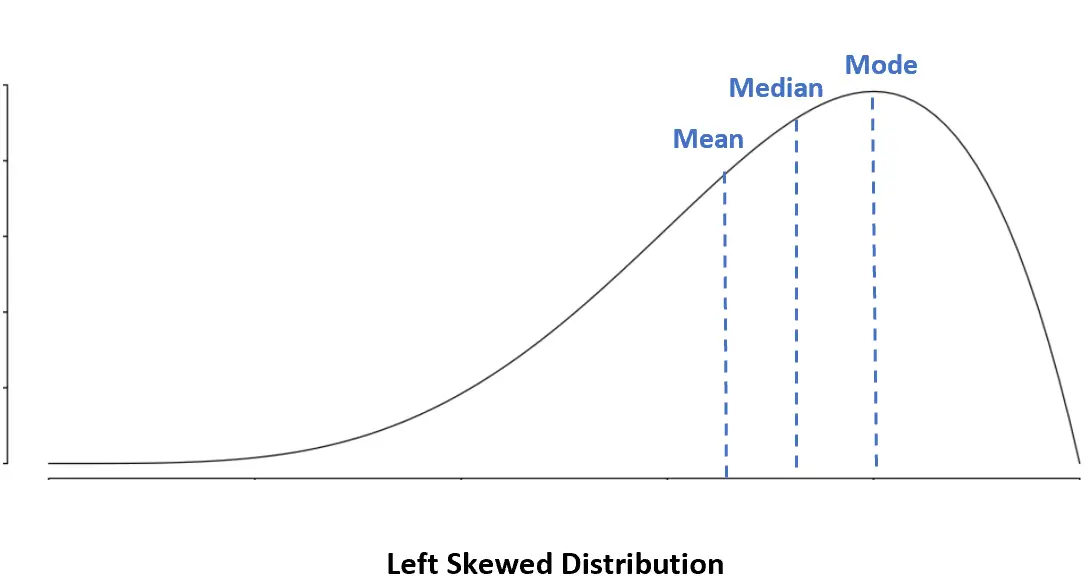
Dalam distribusi condong ke kiri, meannya lebih kecil dari mediannya.
Distribusi miring ke kanan: Mode < Median < Mean
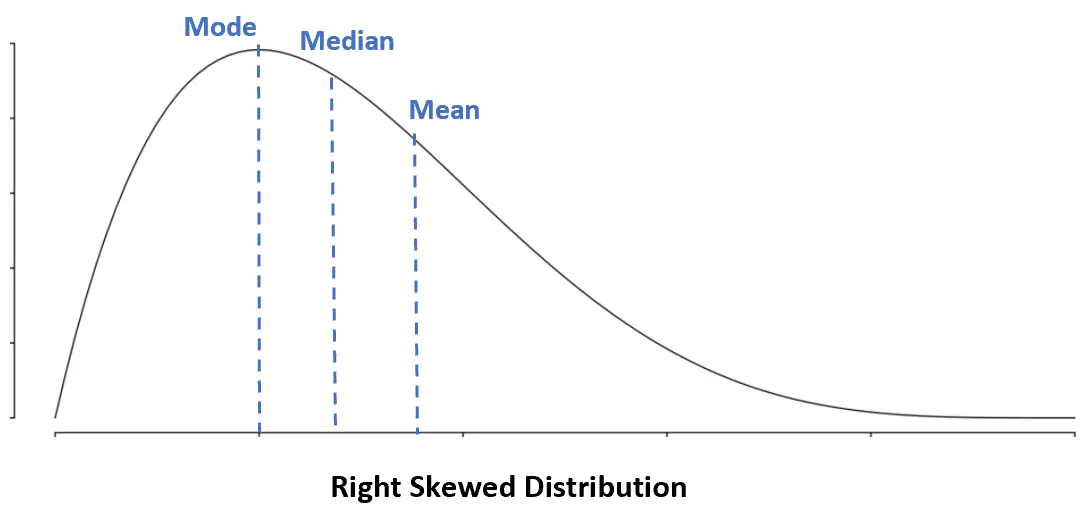
Dalam distribusi miring ke kanan, mean lebih besar dari median.
Tidak ada bias: Mean = Median = Modus

Dalam distribusi simetris, mean, median, dan modus semuanya sama.
Sumber daya tambahan
Distribusi miring ke kiri atau ke kanan
Distribusi simetris: definisi + contoh