Cara melakukan uji-t dua sampel di excel
Uji-t dua sampel digunakan untuk menguji apakah rata-rata dua populasi sama atau tidak.
Tutorial ini menjelaskan cara melakukan uji-t dua sampel di Excel.
Cara melakukan uji-t dua sampel di Excel
Misalkan peneliti ingin mengetahui apakah dua spesies tumbuhan berbeda di suatu negara memiliki rata-rata tinggi yang sama. Karena memerlukan waktu yang terlalu lama untuk berkeliling dan mengukur setiap tanaman, mereka memutuskan untuk mengambil sampel sebanyak 20 tanaman dari setiap spesies.
Gambar berikut menunjukkan tinggi (dalam inci) setiap tanaman di setiap sampel:
Kita dapat melakukan uji-t dua sampel untuk menentukan apakah kedua spesies memiliki rata-rata tinggi yang sama dengan mengikuti langkah-langkah berikut:
Langkah 1: Tentukan apakah varians populasinya sama .
Ketika kita melakukan uji-t dua sampel, pertama-tama kita harus memutuskan apakah kita akan mengasumsikan bahwa kedua populasi mempunyai varian yang sama atau tidak sama. Secara umum, kita dapat berasumsi bahwa suatu populasi mempunyai varians yang sama jika rasio varians sampel terbesar dan varians sampel terkecil kurang dari 4:1.
Kita dapat mencari varians untuk setiap sampel menggunakan fungsi Excel =VAR.S(Cell range) , seperti yang ditunjukkan pada gambar berikut:
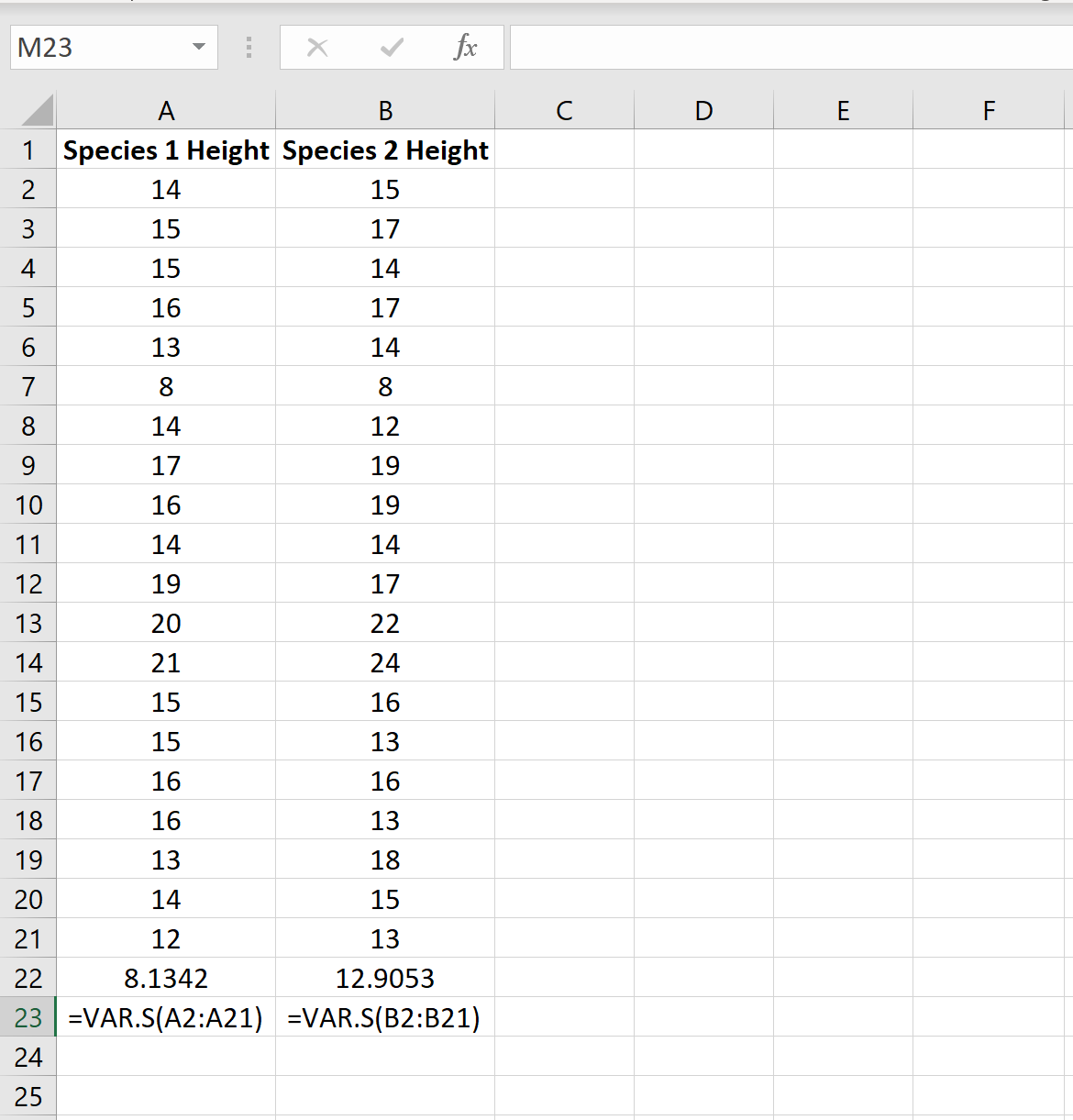
Rasio varians sampel terbesar dan varians sampel terkecil adalah 12.9053/8.1342 = 1.586 , yang kurang dari 4. Artinya kita dapat mengasumsikan bahwa varians populasi adalah sama.
Langkah 2: Buka Analysis ToolPak .
Di tab Data di pita atas, klik “Analisis Data”.
Jika Anda tidak melihat opsi untuk diklik, Anda harus mengunduh Analysis ToolPak terlebih dahulu, yang sepenuhnya gratis.
Langkah 3: Pilih tes yang sesuai untuk digunakan.
Pilih opsi yang bertuliskan uji-t: dua sampel dengan asumsi variansi yang sama , lalu klik OK.
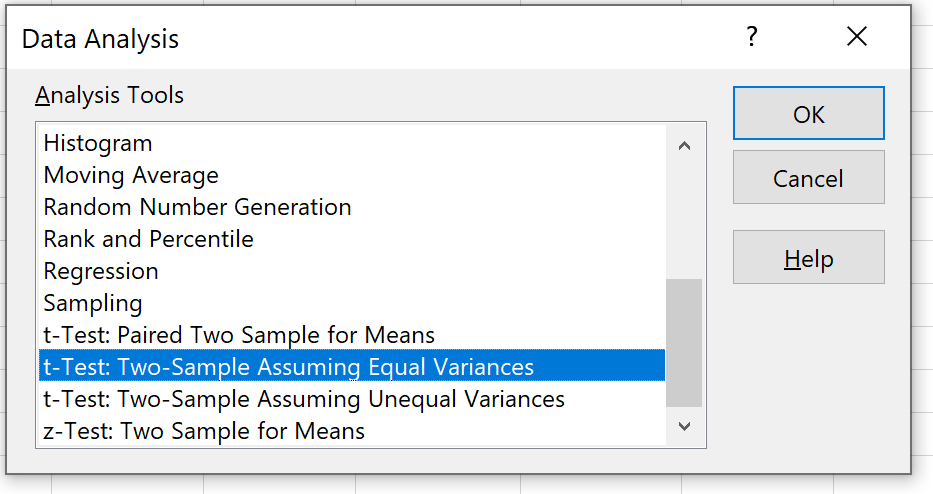
Langkah 4: Masukkan informasi yang diperlukan .
Masukkan rentang nilai untuk variabel 1 (sampel pertama kita), variabel 2 (sampel kedua kita), perbedaan rata-rata hipotetis (dalam hal ini kita beri “0” karena kita ingin mengetahui apakah perbedaan rata-rata populasi sebenarnya adalah 0) , dan rentang keluaran yang ingin kita lihat hasil uji-tnya ditampilkan. Lalu klik oke.
Langkah 5: Tafsirkan hasilnya .
Setelah Anda mengklik OK pada langkah sebelumnya, hasil uji-t akan ditampilkan.
Berikut cara menafsirkan hasilnya:
Rata-rata: Ini adalah rata-rata setiap sampel. Sampel 1 memiliki rata-rata tinggi badan 15,15 dan sampel 2 memiliki rata-rata tinggi badan 15,8 .
Varians: Ini adalah varians untuk setiap sampel. Sampel 1 mempunyai varian sebesar 8,13 dan sampel 2 mempunyai varian sebesar 12,90 .
Observasi: Ini adalah jumlah observasi pada setiap sampel. Kedua sampel berisi 20 observasi (misalnya 20 individu tanaman di setiap sampel).
Varians yang dikumpulkan: angka yang dihitung dengan “menggabungkan” varians setiap sampel menggunakan rumus s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 ] / (n 1 +n 2 – 2), yang ternyata 10.51974 . Angka ini kemudian digunakan saat menghitung statistik uji- t .
Perbedaan Rata-rata Hipotetis: Angka yang kita “hipotesiskan” adalah selisih antara rata-rata kedua populasi. Dalam hal ini kita memilih 0 karena ingin menguji apakah selisih mean kedua populasi sama dengan 0 atau tidak, misalnya tidak ada perbedaan.
df: Derajat kebebasan uji-t, dihitung sebagai n 1 + n 2 -2 = 20 + 20 – 2 = 38 .
t Stat: Statistik uji t , dihitung sebagai t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
Dalam hal ini, t = [15.15-15.8] / √ [10.51974(1/20+1/20)] = -0.63374 .
P(T<=t) dua sisi: nilai p untuk uji t dua sisi. Dalam hal ini, p = 0,530047 . Ini jauh lebih besar dari alpha = 0,05, jadi kita gagal menolak hipotesis nol. Kami tidak mempunyai cukup bukti untuk mengatakan bahwa rata-rata kedua populasi tersebut berbeda.
t Kritis Dua Sisi: Ini adalah nilai kritis pengujian, yang ditemukan dengan mengidentifikasi nilai dalam tabel distribusi t yang berhubungan dengan pengujian dua sisi dengan alpha = 0,05 dan df = 38. Hasilnya adalah 2, 024394 . Karena statistik uji -t kami kurang dari nilai ini, kami gagal menolak hipotesis nol. Kami tidak mempunyai cukup bukti untuk mengatakan bahwa rata-rata kedua populasi tersebut berbeda.
Perhatikan bahwa pendekatan nilai p dan nilai kritis akan menghasilkan kesimpulan yang sama.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan tipe uji-t lainnya di Excel:
Cara melakukan uji-t satu sampel di Excel
Cara melakukan uji-t sampel berpasangan di Excel
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya