Cara melakukan regresi linier berganda di excel

Regresi linier berganda merupakan metode yang dapat kita gunakan untuk memahami hubungan antara dua atau lebih variabel penjelas dan suatu variabel respon .

Tutorial ini menjelaskan cara melakukan regresi linier berganda di Excel.

Catatan: Jika Anda hanya memiliki satu variabel penjelas, Anda sebaiknya melakukan regresi linier sederhana .

Contoh: Regresi Linier Berganda di Excel

Misalkan kita ingin mengetahui apakah jumlah jam yang dihabiskan untuk belajar dan jumlah ujian persiapan yang diambil mempengaruhi nilai yang diperoleh siswa pada ujian masuk perguruan tinggi tertentu.

Untuk mengeksplorasi hubungan ini, kita dapat melakukan regresi linier berganda dengan menggunakan jam belajar dan ujian persiapan yang diambil sebagai variabel penjelas dan hasil ujian sebagai variabel respon.

Selesaikan langkah-langkah berikut di Excel untuk melakukan regresi linier berganda.

Langkah 1: Masukkan datanya.

Masukkan data jumlah jam belajar, ujian persiapan yang diambil, dan hasil ujian yang diterima untuk 20 siswa berikut ini:

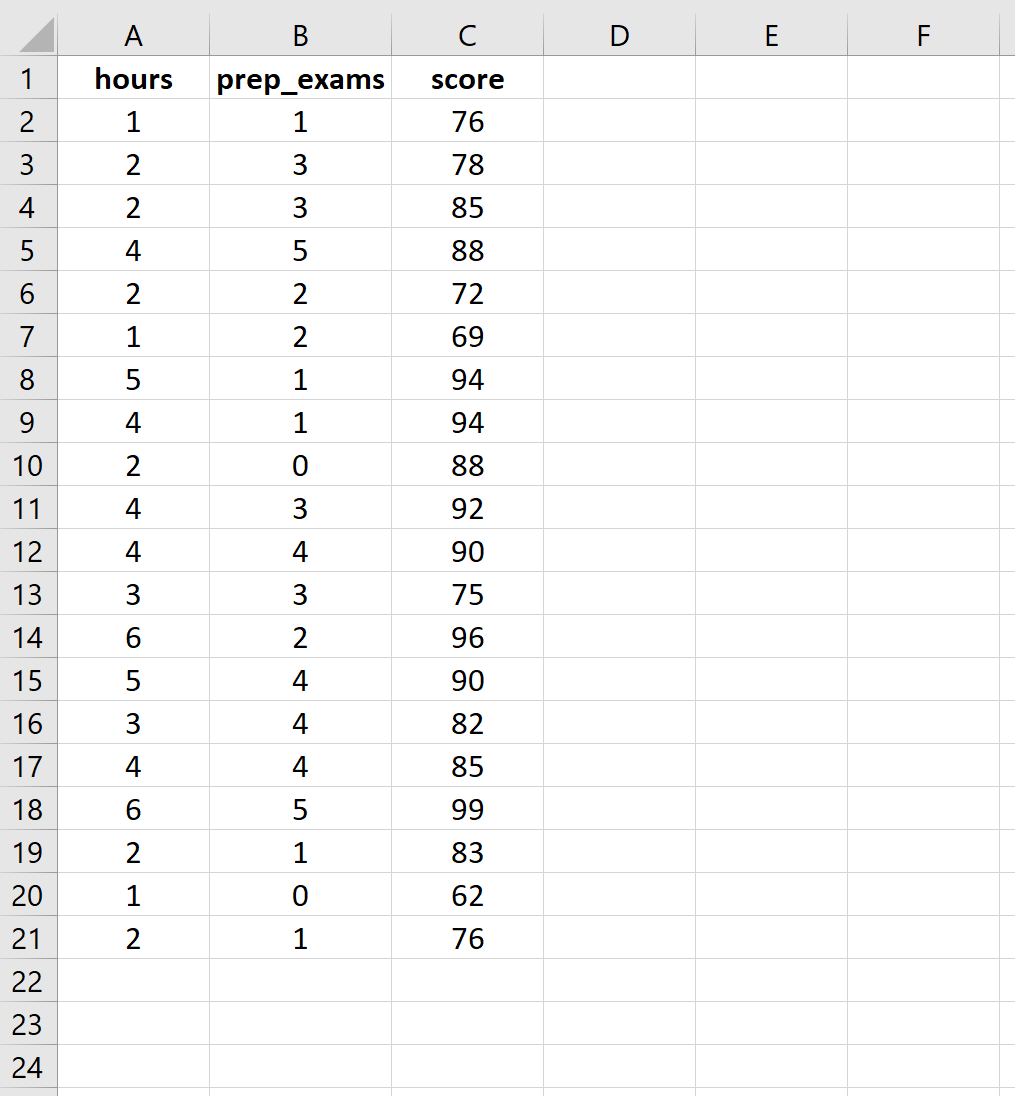
Langkah 2: Lakukan regresi linier berganda.

Di pita atas Excel, buka tab Data dan klik Analisis Data . Jika Anda tidak melihat opsi ini, Anda harus menginstal perangkat lunak Analysis ToolPak gratis terlebih dahulu.

Setelah Anda mengklik Analisis Data, jendela baru akan muncul. Pilih Regresi dan klik OK.

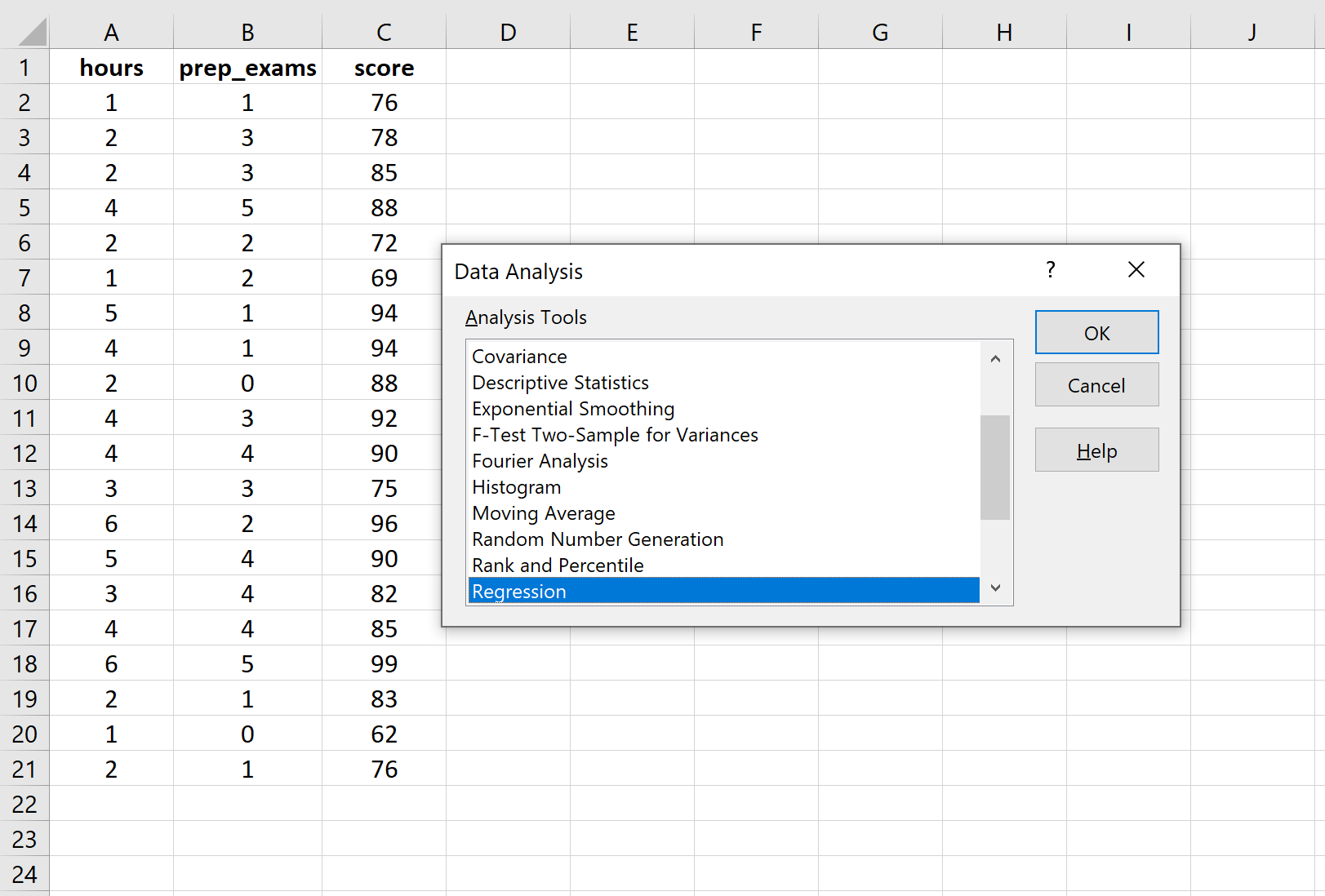
Untuk Input Y Range , isi array nilai untuk variabel respon. Untuk Input X Range , isi array nilai untuk kedua variabel penjelas. Centang kotak di samping Label untuk memberi tahu Excel bahwa kami telah menyertakan nama variabel dalam rentang input. Untuk Rentang Output , pilih sel yang Anda inginkan untuk menampilkan output regresi. Lalu klik oke .

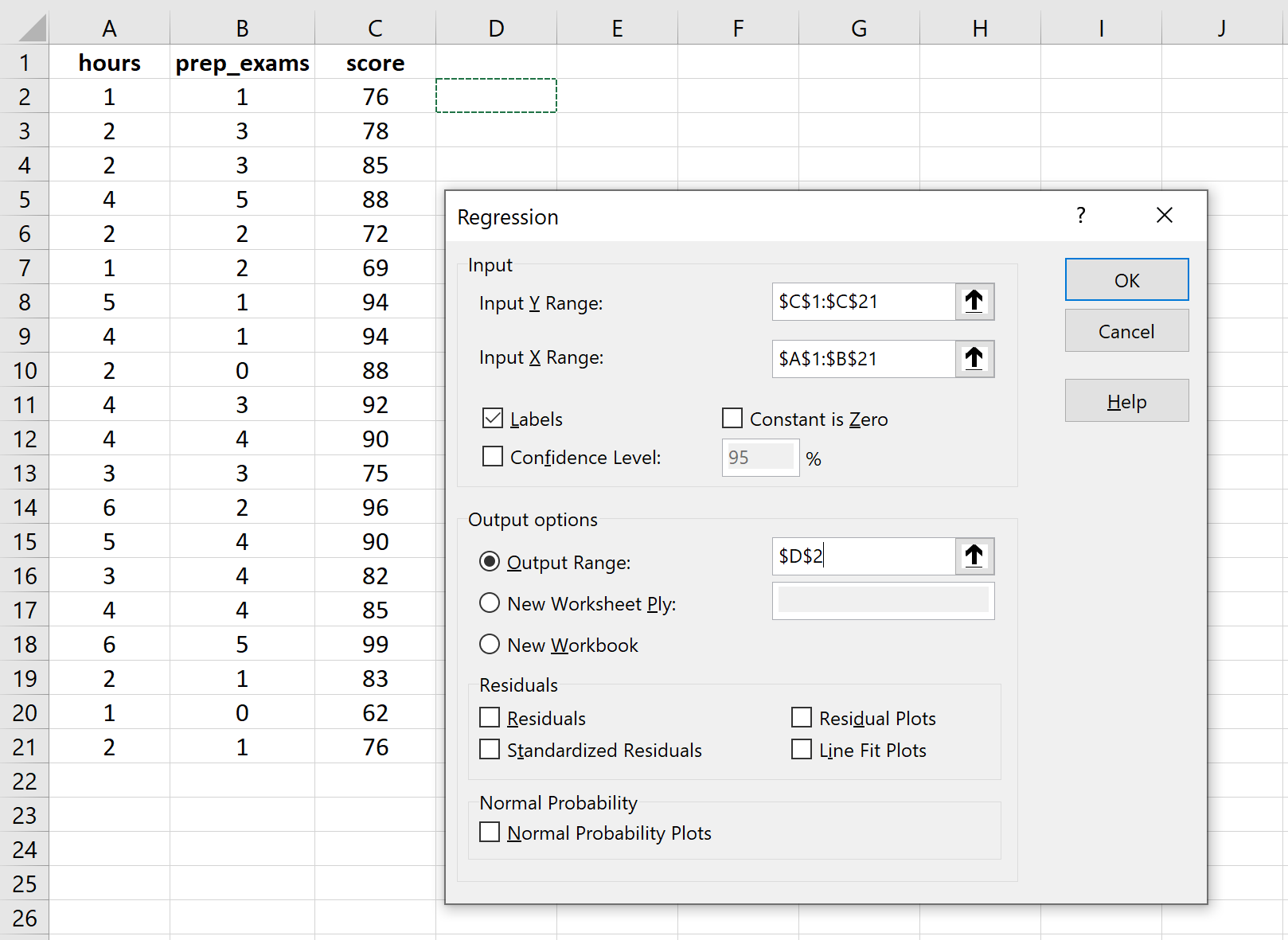
Output berikut akan muncul secara otomatis:

Langkah 3: Tafsirkan hasilnya.

Berikut cara menafsirkan angka paling relevan dalam hasil:

R Persegi: 0,734 . Ini disebut koefisien determinasi. Merupakan proporsi varians variabel respon yang dapat dijelaskan oleh variabel penjelas. Dalam contoh ini, 73,4% variasi nilai ujian dijelaskan oleh jumlah jam belajar dan jumlah persiapan ujian yang diambil.

Kesalahan standar: 5.366 . Ini adalah jarak rata-rata antara nilai yang diamati dan garis regresi. Dalam contoh ini, nilai yang diamati rata-rata menyimpang sebesar 5.366 unit dari garis regresi.

F: 23:46 Ini adalah statistik F keseluruhan untuk model regresi, dihitung sebagai MS regresi/MS sisa.

Arti F: 0,0000 . Ini adalah nilai p yang terkait dengan statistik F keseluruhan. Hal ini memberitahu kita apakah model regresi secara keseluruhan signifikan secara statistik atau tidak. Dengan kata lain, hal ini memberi tahu kita apakah gabungan dua variabel penjelas mempunyai hubungan yang signifikan secara statistik dengan variabel respons. Dalam hal ini, nilai p kurang dari 0,05, menunjukkan bahwa variabel penjelas , jumlah jam belajar , dan persiapan ujian yang diambil digabungkan, memiliki hubungan yang signifikan secara statistik dengan hasil ujian .

Nilai-P. Nilai p individual memberi tahu kita apakah setiap variabel penjelas signifikan secara statistik atau tidak. Kita dapat melihat bahwa jam belajar signifikan secara statistik (p = 0,00) sedangkan ujian persiapan yang diambil (p = 0,52) tidak signifikan secara statistik pada α = 0,05. Karena ujian persiapan sebelumnya tidak signifikan secara statistik, kami mungkin memutuskan untuk menghapusnya dari model.

Koefisien: Koefisien masing-masing variabel penjelas menunjukkan kepada kita perubahan rata-rata yang diharapkan dalam variabel respons, dengan asumsi variabel penjelas lainnya tetap konstan. Misalnya, untuk setiap tambahan jam yang dihabiskan untuk belajar, nilai ujian rata-rata diperkirakan akan meningkat sebesar 5,56 , dengan asumsi bahwa ujian praktik yang diambil tetap konstan.

Berikut cara lain untuk melihatnya: jika Siswa A dan Siswa B sama-sama mengikuti jumlah ujian persiapan yang sama namun Siswa A belajar satu jam lebih lama, maka Siswa A harus memperoleh skor 5,56 poin lebih tinggi daripada siswa B.

Kami menafsirkan koefisien intersep yang berarti bahwa nilai ujian yang diharapkan untuk siswa yang belajar tanpa jam kerja dan tidak mengikuti ujian persiapan adalah 67,67 .

Estimasi persamaan regresi: Kita dapat menggunakan koefisien dari keluaran model untuk membuat estimasi persamaan regresi berikut:

nilai ujian = 67,67 + 5,56*(jam) – 0,60*(ujian persiapan)

Kita dapat menggunakan persamaan regresi perkiraan ini untuk menghitung nilai ujian yang diharapkan seorang siswa, berdasarkan jumlah jam belajar dan jumlah ujian praktik yang mereka ambil. Misalnya, seorang siswa yang belajar selama tiga jam dan mengikuti ujian persiapan harus mendapat nilai 83,75 :

nilai ujian = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Perlu diingat bahwa karena ujian persiapan sebelumnya tidak signifikan secara statistik (p=0,52), kami mungkin memutuskan untuk menghapusnya karena tidak memberikan peningkatan apa pun pada model secara keseluruhan. Dalam hal ini, kita dapat melakukan regresi linier sederhana dengan hanya menggunakan jam belajar sebagai variabel penjelas.

Hasil analisis regresi linier sederhana dapat dilihat di sini .

Sumber daya tambahan

Setelah Anda melakukan regresi linier berganda, Anda mungkin ingin memeriksa beberapa asumsi, termasuk:

1. Pengujian multikolinearitas menggunakan VIF .

2. Uji heterodskedastisitas dengan menggunakan uji Breusch-Pagan .

3. Uji normalitas menggunakan plot QQ .