Frekuensi relatif

Dalam artikel ini Anda akan mempelajari apa itu frekuensi relatif dalam statistik, cara mendapatkan frekuensi relatif, dan dua latihan langkah demi langkah tentang frekuensi relatif.

Berapa frekuensi relatif?

Dalam statistik, frekuensi relatif adalah ukuran yang menunjukkan berapa kali suatu nilai muncul dalam sampel data sebagai proporsi atau persentase. Lebih tepatnya, frekuensi relatif sama dengan frekuensi absolut dibagi dengan jumlah data.

Misalnya, jika frekuensi absolut suatu nilai adalah 15 dan terdapat total 100 titik data, frekuensi relatif dari nilai tersebut adalah 0,15 (15/100=0,15).

Umumnya simbol h _i digunakan untuk menyatakan frekuensi relatif. Meskipun masih belum ada konsensus dalam komunitas statistik, Anda dapat melihat frekuensi relatif diwakili oleh simbol lain.

Cara menghitung frekuensi relatif

Frekuensi relatif sama dengan frekuensi absolut dibagi dengan jumlah data. Oleh karena itu, untuk menghitung frekuensi relatif, Anda harus mencari frekuensi absolut terlebih dahulu, lalu membaginya dengan jumlah observasi.

Jadi rumus frekuensi relatifnya adalah sebagai berikut:

Emas:

• 

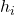
  adalah frekuensi relatif.

• 

  adalah frekuensi absolut.

• 

  adalah jumlah total data.

Sebaliknya, untuk menghitung frekuensi relatif dalam persentase , yaitu frekuensi relatif yang dinyatakan dalam persentase, cukup kalikan rumus sebelumnya dengan 100:

Contoh Frekuensi Relatif

Setelah Anda melihat definisi frekuensi relatif, berikut adalah dua contoh nyata sehingga Anda dapat melihat bagaimana jenis frekuensi ini dihitung. Pada contoh pertama, frekuensi relatif suatu variabel diskrit ditentukan dan pada contoh kedua, variabel kontinu.

Contoh 1: variabel diskrit

• Nilai yang diperoleh pada mata pelajaran statistika pada kelas yang berjumlah 30 siswa adalah sebagai berikut. Berapa frekuensi relatif setiap nada?

Variabel dalam latihan ini bersifat diskrit karena datanya hanya boleh berupa bilangan bulat; oleh karena itu, tidak perlu mengelompokkan data ke dalam interval.

Untuk mencari frekuensi relatif, kita harus menentukan frekuensi absolut terlebih dahulu. Jadi kita membuat tabel frekuensi dan menghitung frekuensi absolut untuk setiap nilai yang berbeda:

Sekarang kita telah menghitung frekuensi absolut, kita dapat menghitung frekuensi relatif. Untuk melakukannya, cukup bagi setiap frekuensi absolut dengan jumlah total data (30):

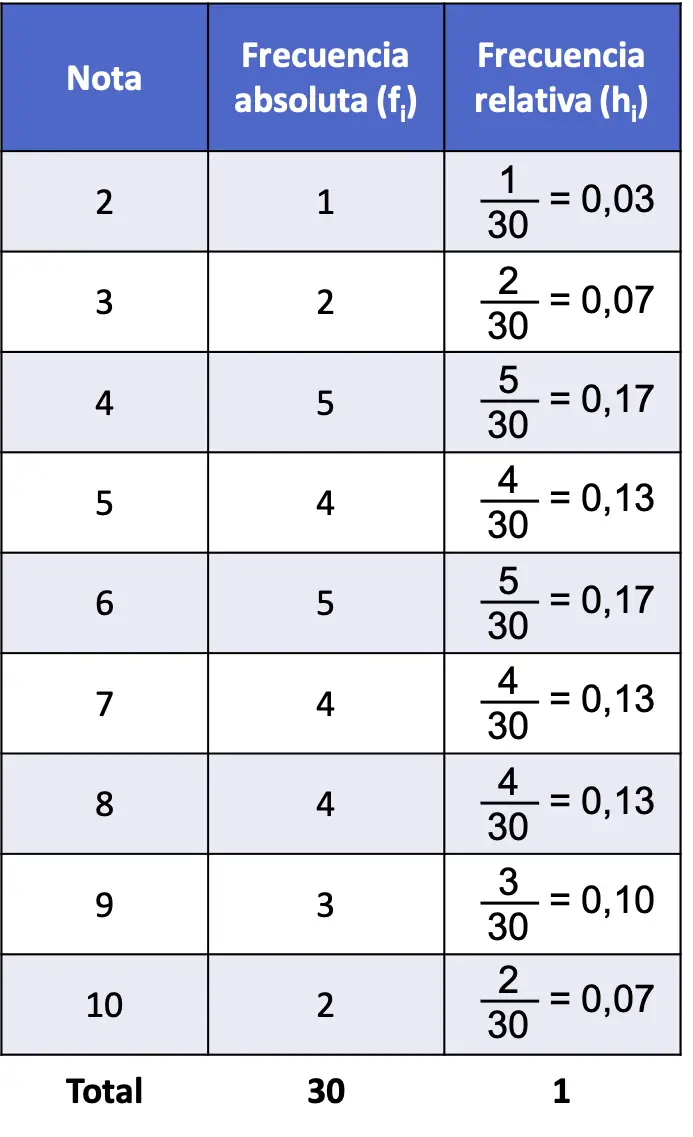
Jadi, tabel frekuensi permasalahan dengan frekuensi absolut dan frekuensi relatif adalah sebagai berikut:

Perhatikan bahwa jumlah semua frekuensi relatif selalu menghasilkan 1, jika tidak, ini berarti beberapa perhitungan salah.

Contoh 2: variabel kontinu

• Tinggi badan 20 orang diukur dan diperoleh hasil yang disebutkan di bawah ini. Pisahkan data menjadi beberapa interval dan temukan frekuensi relatif setiap interval.

Data dalam sampel statistik ini termasuk dalam variabel kontinu, karena bersifat desimal sehingga variabel tersebut dapat mengambil nilai apa pun. Jadi sebelum melakukan perhitungan frekuensi, kita kelompokkan dulu datanya ke dalam interval-interval dengan amplitudo 10 persepuluh.

Selanjutnya kita buat tabel frekuensi dengan frekuensi absolut tiap interval:

Dan setelah kita menemukan frekuensi absolutnya, kita bisa mendapatkan frekuensi relatif setiap interval dengan membagi frekuensi absolutnya dengan jumlah total data (20):

Frekuensi relatif kumulatif

Seperti namanya, frekuensi relatif kumulatif adalah jenis frekuensi lain yang digunakan dalam statistik dan dihitung dari frekuensi relatif.

Lebih tepatnya, frekuensi relatif kumulatif suatu nilai sama dengan jumlah frekuensi relatif dari nilai itu sendiri ditambah frekuensi relatif dari semua nilai yang lebih kecil.

Agar Anda dapat melihat bagaimana frekuensi relatif kumulatif diperoleh, frekuensi relatif kumulatif dari dataset pada contoh pertama telah dihitung di bawah ini: