Cara menggunakan fungsi lm() di r agar sesuai dengan model linier

Fungsi lm() di R digunakan untuk menyesuaikan model regresi linier.

Fungsi ini menggunakan sintaks dasar berikut:

lm(rumus, data,…)

Emas:

• rumus : Rumus model linier (misal y ~ x1 + x2)
• data: Nama blok data yang berisi data

Contoh berikut menunjukkan cara menggunakan fungsi ini di R untuk melakukan hal berikut:

• Cocokkan model regresi
• Lihat ringkasan kesesuaian model regresi
• Lihat plot diagnostik model
• Plot model regresi yang sesuai
• Buat prediksi menggunakan model regresi

Sesuaikan model regresi

Kode berikut menunjukkan cara menggunakan fungsi lm() agar sesuai dengan model regresi linier di R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Tampilkan ringkasan model regresi

Kita kemudian dapat menggunakan fungsi ringkasan() untuk menampilkan ringkasan kesesuaian model regresi:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

Berikut cara menginterpretasikan nilai terpenting dalam model:

• F-statistik = 18,35, nilai p yang sesuai = 0,002675. Karena nilai p ini kurang dari 0,05, model secara keseluruhan signifikan secara statistik.
• Kelipatan R kuadrat = 0,6964. Hal ini menunjukkan bahwa 69,64% variasi variabel respon y dapat dijelaskan oleh variabel prediktor x.
• Estimasi koefisien x : 1,2780. Hal ini menunjukkan bahwa setiap kenaikan unit tambahan pada x dikaitkan dengan peningkatan rata-rata sebesar 1,2780 pada y.

Kita kemudian dapat menggunakan estimasi koefisien dari output untuk menulis persamaan regresi estimasi:

kamu = 11,1432 + 1,2780*(x)

Bonus : Anda dapat menemukan panduan lengkap untuk menafsirkan setiap nilai keluaran regresi di R di sini .

Lihat plot diagnostik model

Kita kemudian dapat menggunakan fungsi plot() untuk memplot plot diagnostik model regresi:

 #create diagnostic plots
plot(model) 

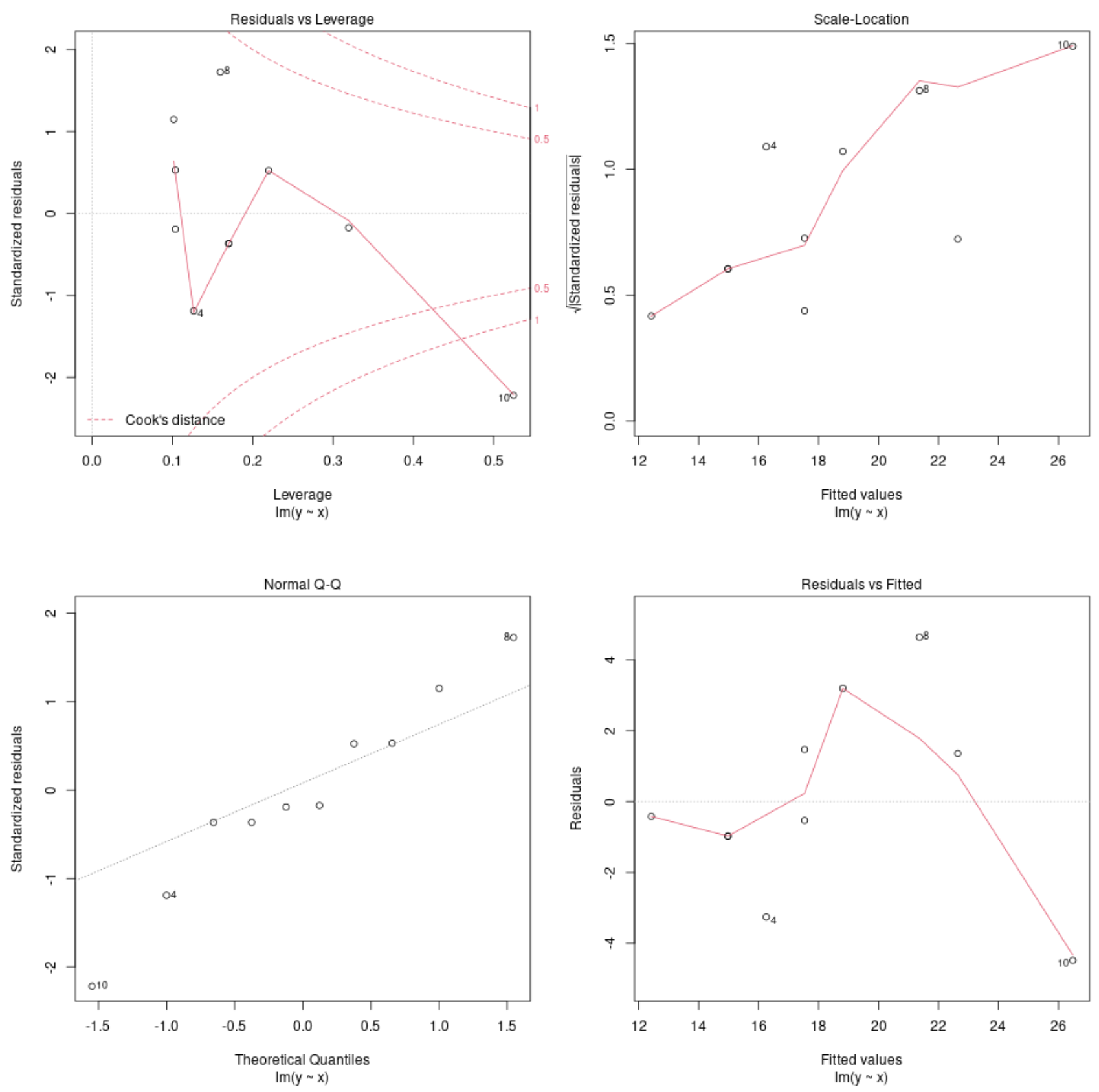
Grafik ini memungkinkan kita menganalisis sisa model regresi untuk menentukan apakah model tersebut sesuai digunakan untuk data.

Lihat tutorial ini untuk penjelasan lengkap tentang cara menafsirkan plot diagnostik model di R.

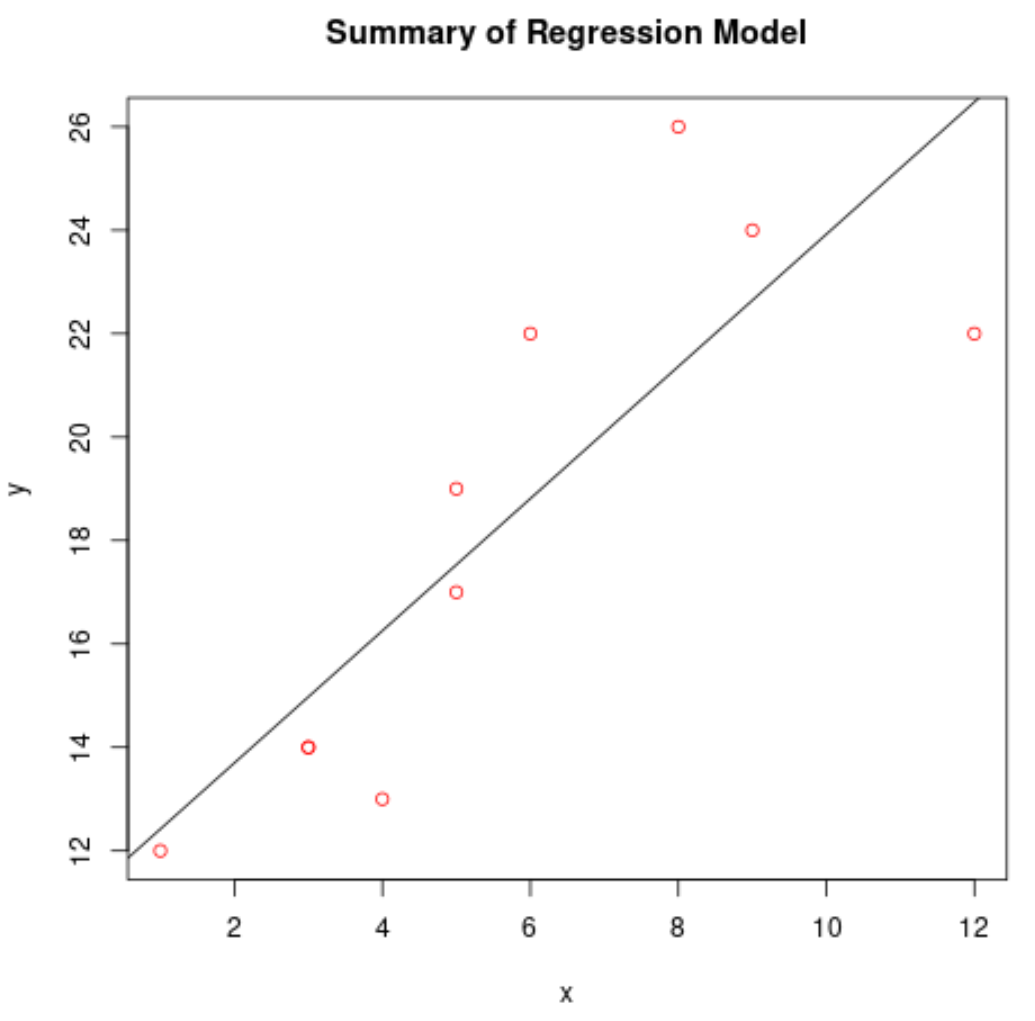
Plot model regresi yang sesuai

Kita dapat menggunakan fungsi abline() untuk memplot model regresi yang sesuai:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

Gunakan model regresi untuk membuat prediksi

Kita dapat menggunakan fungsi prediksi() untuk memprediksi nilai respons observasi baru:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

Model tersebut memperkirakan observasi baru ini akan memiliki nilai respon sebesar 17.5332 .

Sumber daya tambahan

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi bertahap di R