Cara menggunakan geometpdf() dan geometcdf() pada kalkulator ti-84

Distribusi geometri menggambarkan peluang mengalami sejumlah kegagalan tertentu sebelum mengalami keberhasilan pertama dalam serangkaian percobaan dengan ciri-ciri sebagai berikut:

• Hanya ada dua kemungkinan hasil: sukses atau gagal.
• Kemungkinan keberhasilannya sama di setiap percobaan.

Jika suatu variabel acak X mengikuti distribusi geometri, maka peluang mengalami k kegagalan sebelum mengalami keberhasilan pertama dapat dicari dengan rumus berikut:

P(X=k) = (1-p) ^kp

Emas:

• k : jumlah kegagalan sebelum kesuksesan pertama
• p : probabilitas keberhasilan pada setiap percobaan

Probabilitas kumulatif kita mengalami k atau lebih sedikit kegagalan hingga keberhasilan pertama dapat dicari dengan menggunakan rumus berikut:

P(X≤k) = 1 – (1-p) ^k+1

Untuk menghitung probabilitas yang terkait dengan distribusi geometri pada kalkulator TI-84, Anda dapat menggunakan fungsi berikut:

• geometpdf (probabilitas, tes)
• geometcdf(probabilitas, tes)

Contoh berikut menunjukkan cara menggunakan masing-masing fungsi ini dalam praktiknya.

Contoh 1: Cara menggunakan geometpdf()

Misalkan seorang peneliti menunggu di luar perpustakaan untuk menanyakan orang-orang apakah mereka mendukung undang-undang tertentu. Peluang seseorang mendukung hukum adalah p = 0,2. Berapa probabilitas bahwa orang keempat yang diajak bicara oleh peneliti akan menjadi orang pertama yang mendukung undang-undang tersebut?

Untuk menjawab pertanyaan ini, kita dapat menggunakan fungsi geometpdf() .

Tekan ke-2 lalu tekan VARS . Gulir ke geometpdf() dan tekan ENTER .

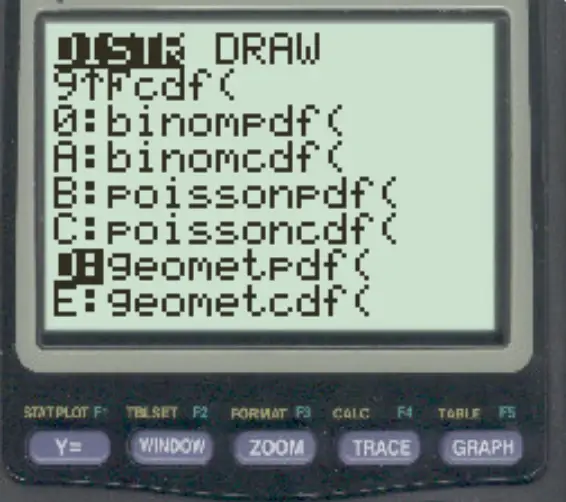
Kemudian ketik nilai berikut dan tekan ENTER .

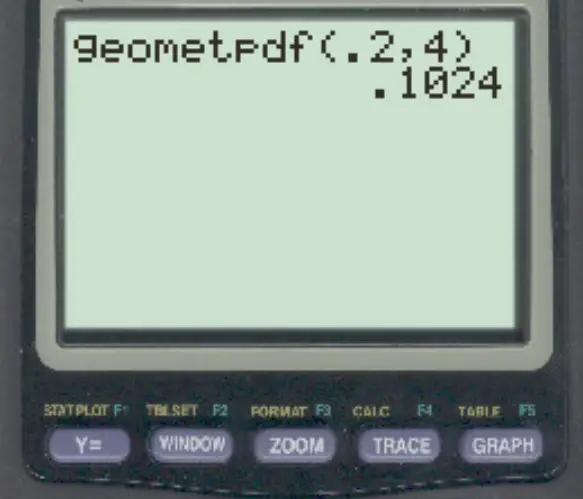
Peluang orang keempat yang diajak bicara peneliti adalah orang pertama yang mendukung undang-undang tersebut adalah 0,1024 .

Contoh 2: Cara menggunakan geometcdf()

Misalkan kita mengetahui bahwa 4% orang yang mengunjungi bankir tertentu menyatakan bangkrut. Berapa peluang bankir tersebut bertemu kurang dari 9 orang sebelum bertemu dengan seseorang yang menyatakan pailit?

Untuk menjawab pertanyaan ini, kita dapat menggunakan fungsi geometcdf() .

Tekan ke-2 lalu tekan VARS . Gulir ke bawah ke geometcdf() dan tekan ENTER .

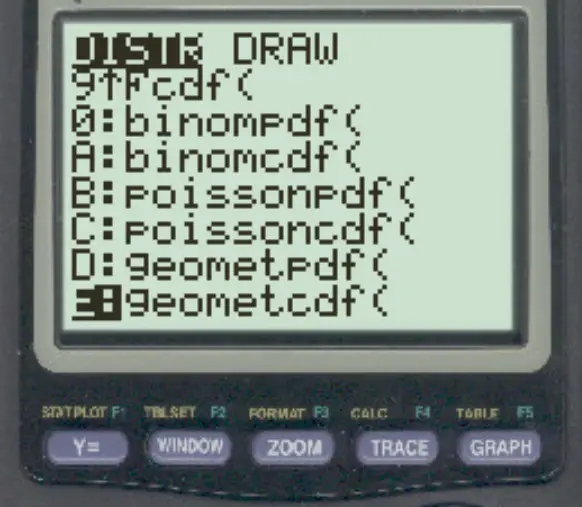
Kemudian ketik nilai berikut dan tekan ENTER .

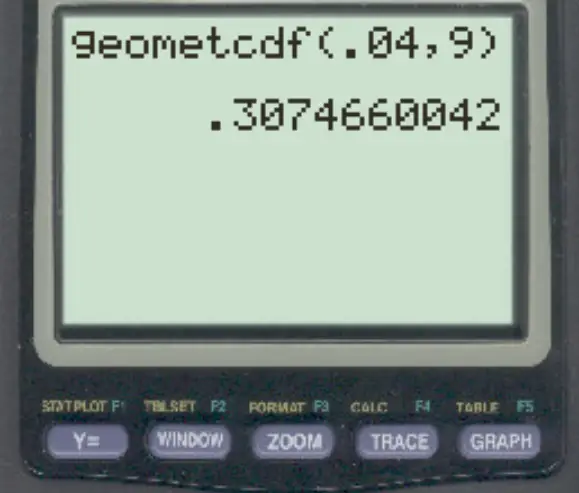
Peluang seorang bankir bertemu kurang dari 9 orang sebelum bertemu dengan seseorang yang menyatakan pailit adalah 0,307466 .

Bonus: Jangan ragu untuk menggunakan kalkulator distribusi geometri online ini untuk mengonfirmasi hasil Anda.

Sumber daya tambahan

Cara Menghitung Probabilitas Normal pada Kalkulator TI-84
Cara Menghitung Probabilitas Binomial pada Kalkulator TI-84
Cara Menghitung Probabilitas Poisson pada Kalkulator TI-84