Bagaimana cara memeriksa asumsi anova

ANOVA satu arah adalah uji statistik yang digunakan untuk menentukan ada atau tidaknya perbedaan yang signifikan antara rata-rata tiga atau lebih kelompok independen.

Berikut adalah contoh kapan kita dapat menggunakan ANOVA satu arah:

Anda secara acak membagi kelas yang terdiri dari 90 siswa menjadi tiga kelompok yang terdiri dari 30 orang. Setiap kelompok menggunakan teknik belajar yang berbeda selama sebulan untuk mempersiapkan ujian. Pada akhir bulan, semua siswa mengikuti ujian yang sama.

Anda ingin tahu apakah teknik belajar berdampak pada nilai ujian atau tidak. Jadi, Anda melakukan ANOVA satu arah untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara skor rata-rata ketiga kelompok.

Sebelum kita dapat melakukan ANOVA satu arah, pertama-tama kita harus memverifikasi bahwa tiga asumsi terpenuhi.

1. Normalitas – Setiap sampel diambil dari populasi yang berdistribusi normal.

2. Varians yang sama – Varians dari populasi yang dijadikan sampel adalah sama.

3. Independensi – Pengamatan dalam setiap kelompok tidak bergantung satu sama lain dan pengamatan dalam kelompok diperoleh dengan pengambilan sampel secara acak.

Jika asumsi ini tidak terpenuhi, hasil ANOVA satu arah kami mungkin tidak dapat diandalkan.

Dalam artikel ini kami menjelaskan cara memeriksa asumsi-asumsi tersebut dan apa yang harus dilakukan jika ada asumsi yang dilanggar.

Asumsi #1: normalitas

ANOVA mengasumsikan bahwa setiap sampel diambil dari populasi yang berdistribusi normal.

Cara memeriksa hipotesis ini di R:

Untuk memverifikasi hipotesis ini, kita dapat menggunakan dua pendekatan:

• Verifikasi hipotesis secara visual menggunakan histogram atau plot QQ .
• Verifikasi hipotesis menggunakan uji statistik formal seperti Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre atau D’Agostino-Pearson.

Misalnya, kita merekrut 90 orang untuk berpartisipasi dalam eksperimen penurunan berat badan, yang mana kita secara acak menugaskan 30 orang untuk mengikuti Program A, Program B, atau Program C selama satu bulan. Untuk melihat apakah program ini berdampak pada penurunan berat badan, kami ingin melakukan ANOVA satu arah. Kode berikut menunjukkan cara memeriksa asumsi normalitas menggunakan histogram, plot QQ, dan uji Shapiro-Wilk.

1. Sesuaikan model ANOVA.

 #make this example reproducible
set.seed(0)

#create data frame
data <- data. frame (program = rep(c(" A ", " B ", " C "), each = 30 ),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Buat histogram nilai respon.

 #create histogram
hist(data$weight_loss)

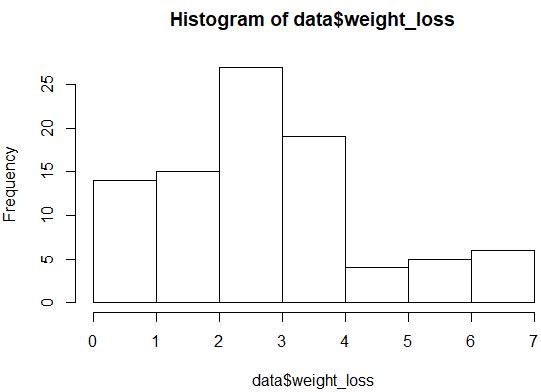
Distribusinya tidak terlihat terdistribusi secara normal (misalnya tidak berbentuk “lonceng”), namun kita juga dapat membuat plot QQ untuk melihat distribusinya lagi.

3. Buat plot residu QQ

 #create QQ plot to compare this dataset to a theoretical normal distribution
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals) 

Secara umum, jika titik-titik data terletak di sepanjang garis diagonal lurus pada plot QQ, kemungkinan besar kumpulan data tersebut mengikuti distribusi normal. Dalam hal ini, kita dapat melihat adanya penyimpangan yang nyata dari garis di sepanjang ujungnya, yang dapat menunjukkan bahwa data tidak terdistribusi secara normal.

4. Lakukan uji normalitas Shapiro-Wilk.

 #Conduct Shapiro-Wilk Test for normality
shapiro. test (data$weight_loss)

#Shapiro-Wilk normality test
#
#data: data$weight_loss
#W = 0.9587, p-value = 0.005999

Uji Shapiro-Wilk menguji hipotesis nol bahwa sampel berasal dari distribusi normal terhadap hipotesis alternatif bahwa sampel tidak berasal dari distribusi normal. Dalam hal ini, nilai p tes tersebut adalah 0,005999 , yang lebih rendah dari tingkat alfa sebesar 0,05. Hal ini menunjukkan bahwa sampel tidak mengikuti distribusi normal.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi:

Secara umum, ANOVA satu arah dianggap cukup kuat terhadap pelanggaran asumsi normalitas selama ukuran sampelnya cukup besar.

Selain itu, jika Anda memiliki sampel yang sangat besar, uji statistik seperti uji Shapiro-Wilk hampir selalu memberi tahu Anda bahwa data Anda tidak normal. Oleh karena itu, sebaiknya periksa data Anda secara visual menggunakan bagan seperti histogram dan plot QQ. Dengan hanya melihat grafik saja anda sudah bisa mendapatkan gambaran yang cukup baik apakah datanya terdistribusi normal atau tidak.

Jika asumsi normalitas sangat dilanggar atau Anda hanya ingin bersikap konservatif, Anda punya dua pilihan:

(1) Transformasikan nilai respon data Anda agar distribusinya lebih terdistribusi secara normal.

(2) Melakukan uji nonparametrik yang setara seperti uji Kruskal-Wallis yang tidak memerlukan asumsi normalitas.

Asumsi #2: varians yang sama

ANOVA mengasumsikan bahwa varians populasi dari mana sampel diambil adalah sama.

Cara memeriksa hipotesis ini di R:

Kita dapat memverifikasi hipotesis ini di R menggunakan dua pendekatan:

• Verifikasi hipotesis secara visual menggunakan diagram kotak.
• Uji hipotesis menggunakan uji statistik formal seperti uji Bartlett.

Kode berikut menunjukkan cara melakukan ini, menggunakan kumpulan data penurunan berat badan palsu yang sama yang kita buat sebelumnya.

1. Buat plot kotak.

 #Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab=' Program ', ylab=' Weight Loss ', data=data)

Variasi penurunan berat badan pada masing-masing kelompok dapat diamati dari panjang setiap boxplot. Semakin panjang kotaknya, semakin tinggi variansnya. Misalnya, kita dapat melihat bahwa variansnya sedikit lebih tinggi pada peserta Program C dibandingkan dengan Program A dan Program B.

2. Lakukan tes Bartlett.

 #Create box plots that show distribution of weight loss for each group
bartlett. test (weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data: weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Uji Bartlett menguji hipotesis nol bahwa sampel mempunyai varians yang sama terhadap hipotesis alternatif bahwa sampel tidak mempunyai varians yang sama. Dalam hal ini, nilai p tes tersebut adalah 0,01599 , yang lebih rendah dari tingkat alfa sebesar 0,05. Hal ini menunjukkan bahwa tidak semua sampel mempunyai varian yang sama.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi:

Secara umum, ANOVA satu arah dianggap cukup kuat terhadap pelanggaran asumsi variansi yang sama selama masing-masing kelompok memiliki ukuran sampel yang sama.

Namun, jika ukuran sampel tidak sama dan asumsi ini sangat dilanggar, Anda dapat menjalankan uji Kruskal-Wallis , yang merupakan versi non-parametrik dari ANOVA satu arah.

Asumsi #3: Kemerdekaan

ANOVA mengasumsikan:

• Pengamatan masing-masing kelompok tidak bergantung pada pengamatan semua kelompok lainnya.
• Pengamatan pada masing-masing kelompok diperoleh dengan sampel acak.

Cara memverifikasi hipotesis ini:

Tidak ada tes formal yang dapat Anda gunakan untuk memverifikasi bahwa observasi di setiap kelompok bersifat independen dan diperoleh melalui sampel acak. Satu-satunya cara untuk memenuhi asumsi ini adalah dengan menggunakan rancangan acak.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi:

Sayangnya, tidak banyak yang dapat Anda lakukan jika asumsi tersebut tidak terpenuhi. Sederhananya, jika data dikumpulkan sedemikian rupa sehingga observasi pada setiap kelompok tidak independen terhadap observasi pada kelompok lain, atau jika observasi pada setiap kelompok tidak diperoleh melalui proses acak, maka hasil ANOVA tidak akan dapat diandalkan. .

Jika asumsi ini tidak terpenuhi, hal terbaik yang dilakukan adalah membuat ulang percobaan menggunakan rancangan acak.

Bacaan lebih lanjut:

Bagaimana melakukan ANOVA satu arah di R
Bagaimana Melakukan ANOVA Satu Arah di Excel