Lima hipotesis korelasi pearson
Koefisien korelasi Pearson (juga dikenal sebagai “koefisien korelasi momen produk”) mengukur hubungan linier antara dua variabel.
Itu selalu mengambil nilai antara -1 dan 1 di mana:
- -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
- 0 menunjukkan tidak ada korelasi linier antara dua variabel
- Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel
Namun, sebelum menghitung koefisien korelasi Pearson antara dua variabel, kita harus memastikan bahwa lima asumsi terpenuhi:
1. Tingkat pengukuran: Kedua variabel harus diukur pada tingkat interval atau rasio .
2. Hubungan linier : Harus ada hubungan linier antara kedua variabel.
3. Normalitas: kedua variabel harus mempunyai distribusi mendekati normal.
4. Pasangan terkait: Setiap observasi dalam kumpulan data harus memiliki sepasang nilai.
5. Tidak ada outlier: Tidak boleh ada outlier ekstrim dalam kumpulan data.
Pada artikel ini kami memberikan penjelasan masing-masing asumsi serta cara menentukan apakah asumsi tersebut terpenuhi.
Hipotesis 1: Tingkat pengukuran
Untuk menghitung koefisien korelasi Pearson antara dua variabel, kedua variabel harus diukur pada tingkat interval atau rasio .
Grafik berikut memberikan penjelasan singkat tentang empat tingkatan di mana variabel dapat diukur:
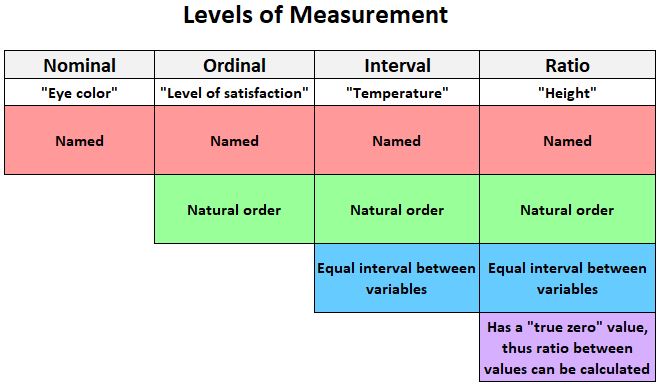
Berikut beberapa contoh variabel yang dapat diukur dalam skala interval :
- Suhu: Diukur dalam Fahrenheit atau Celsius
- Nilai kredit: diukur dari 300 hingga 850
- Skor SAT: diukur dari 400 hingga 1.600
Berikut beberapa contoh variabel yang dapat diukur dengan skala rasio :
- Tinggi: Diukur dalam sentimeter, inci, kaki, dll.
- Berat: diukur dalam kilogram, pon, dll.
- Panjang: Diukur dalam sentimeter, inci, kaki, dll.
Jika variabel diukur pada tingkat ordinal , maka Anda perlu menghitung koefisien korelasi Spearman di antara variabel tersebut.
Terkait: Tingkatan Pengukuran: Nominal, Ordinal, Interval, dan Rasio
Hipotesis 2: Hubungan linier
Untuk menghitung koefisien korelasi Pearson antara dua variabel, harus ada hubungan linier antara kedua variabel.
Cara termudah untuk menguji hipotesis ini adalah dengan membuat diagram sebar kedua variabel. Jika titik-titik pada plot kira-kira mengikuti garis lurus, maka terdapat hubungan linier:
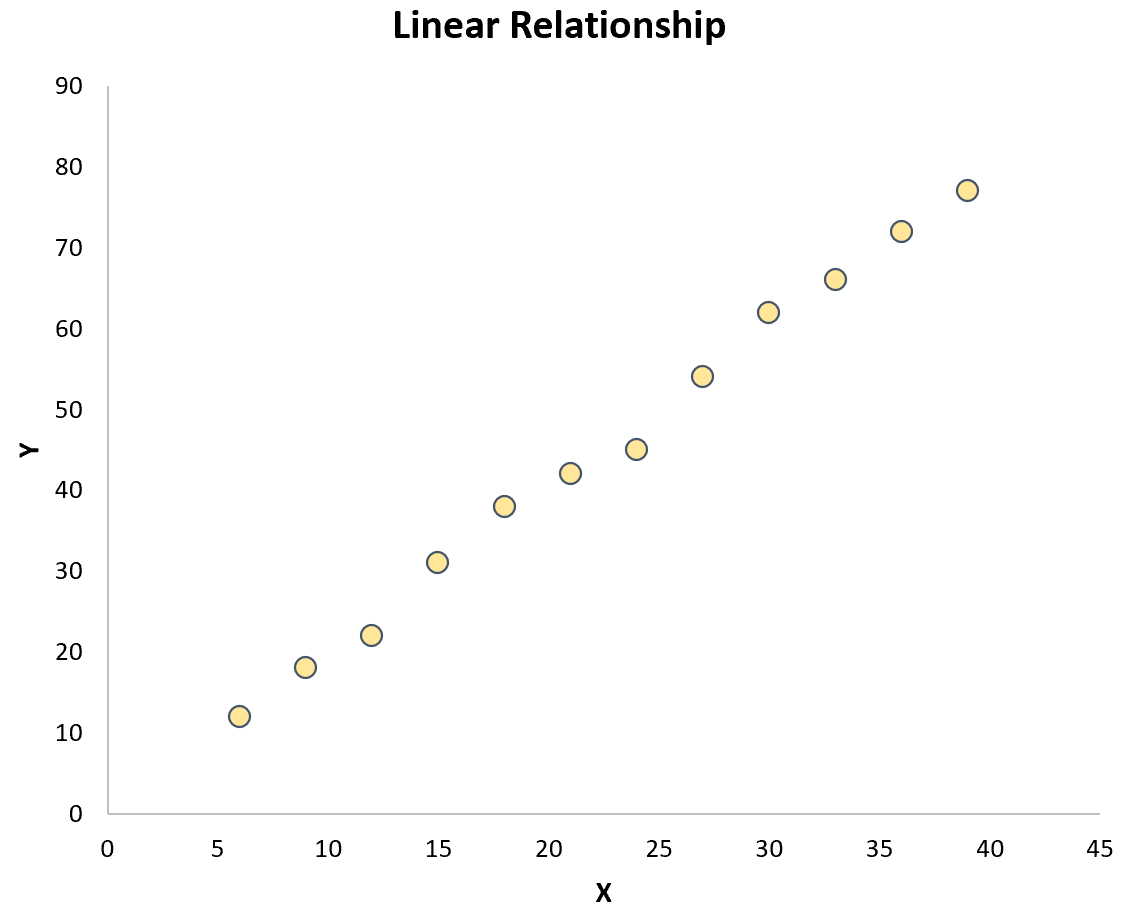
Namun, jika titik-titik tersebut tersebar secara acak di seluruh plot atau memiliki jenis hubungan lain (seperti kuadrat), maka tidak ada hubungan linier antar variabel:
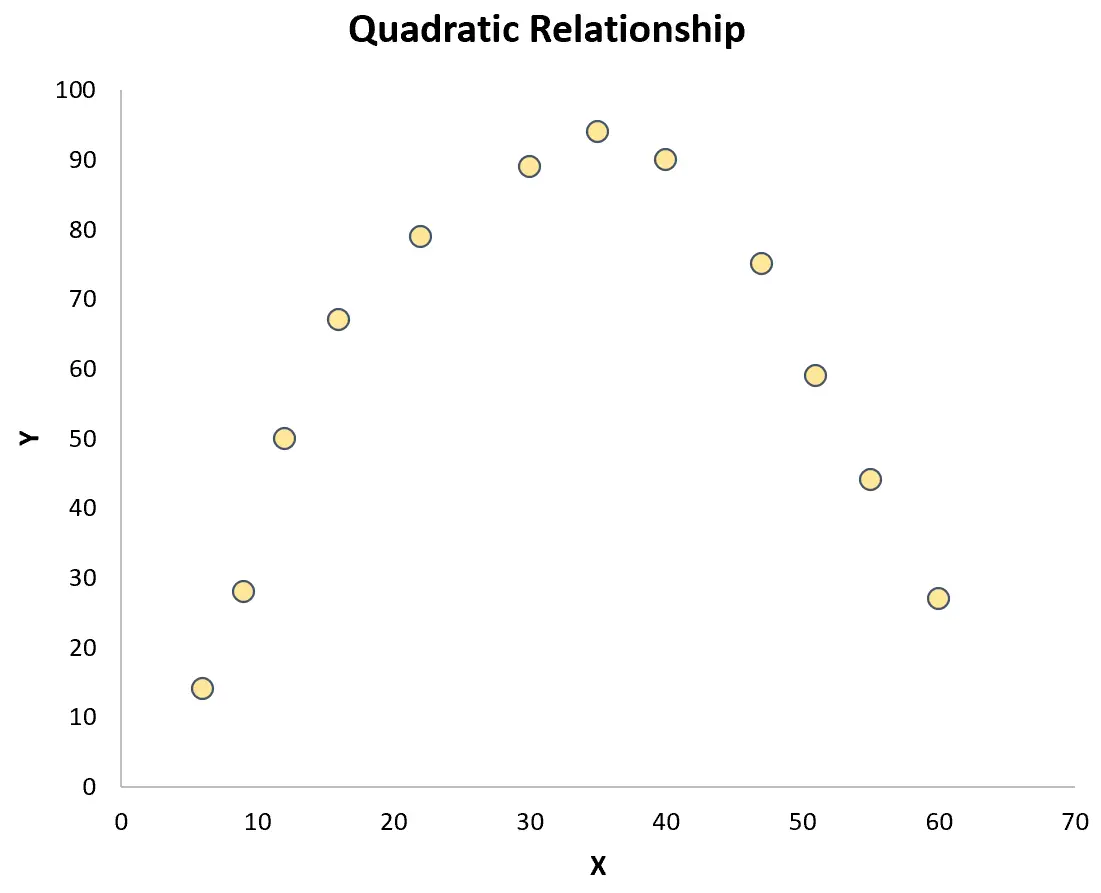
Dalam hal ini, koefisien korelasi Pearson tidak akan cukup menggambarkan hubungan antar variabel.
Hipotesis 3: normalitas
Koefisien korelasi Pearson juga mengasumsikan bahwa kedua variabel tersebut berdistribusi normal .
Anda dapat memverifikasi asumsi ini secara visual dengan membuat histogram atau plot QQ untuk setiap variabel.
1. Histogram
Jika histogram suatu kumpulan data kira-kira berbentuk lonceng, kemungkinan besar data tersebut terdistribusi secara normal.

2. Tanah QQ
Plot QQ, kependekan dari “quantile-quantile”, adalah jenis plot yang menampilkan kuantil teoretis di sepanjang sumbu x (yaitu lokasi data Anda jika mengikuti distribusi normal) dan kuantil sampel di sepanjang sumbu y. (yaitu di mana data Anda sebenarnya berada).
Jika nilai data mengikuti garis kira-kira lurus membentuk sudut 45 derajat, maka data dianggap berdistribusi normal.

Anda juga dapat melakukan uji statistik formal untuk menentukan apakah suatu variabel terdistribusi normal.
Jika nilai p tes berada di bawah tingkat signifikansi tertentu (misalnya α = 0,05), maka Anda mempunyai cukup bukti untuk mengatakan bahwa data tidak terdistribusi normal.
Ada tiga uji statistik yang biasa digunakan untuk menguji normalitas:
1. Tes Jarque-Bera
- Cara Melakukan Tes Jarque-Bera di Excel
- Cara melakukan tes Jarque-Bera di R
- Cara melakukan tes Jarque-Bera dengan Python
2. Tes Shapiro-Wilk
3. Tes Kolmogorov-Smirnov
Hipotesis 4: Pasangan yang berkerabat
Koefisien korelasi Pearson juga mengasumsikan bahwa setiap observasi dalam kumpulan data harus memiliki sepasang nilai.
Hipotesis ini mudah untuk diverifikasi. Misalnya, jika Anda menghitung korelasi antara berat badan dan tinggi badan, cukup verifikasi bahwa setiap observasi dalam kumpulan data memiliki ukuran berat badan dan ukuran tinggi badan.
Hipotesis 5: Tidak ada outlier
Koefisien korelasi Pearson juga mengasumsikan tidak terdapat outlier yang ekstrim pada kumpulan data, karena outlier sangat mempengaruhi penghitungan koefisien korelasi.
Untuk mengilustrasikannya, pertimbangkan kumpulan data berikut:
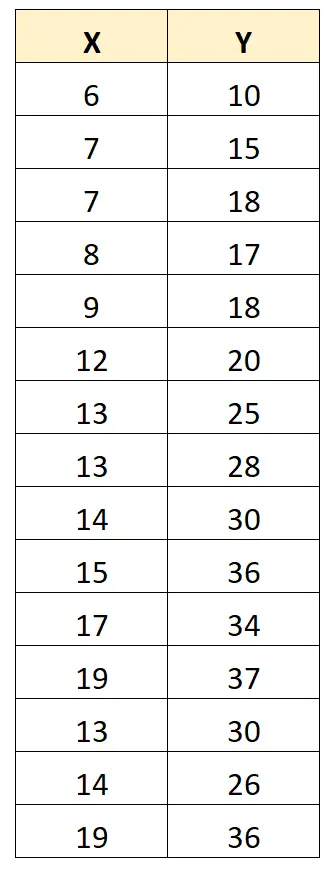
Koefisien korelasi Pearson antara X dan Y sebesar 0,949 .
Namun, misalkan kita memiliki outlier dalam kumpulan data:
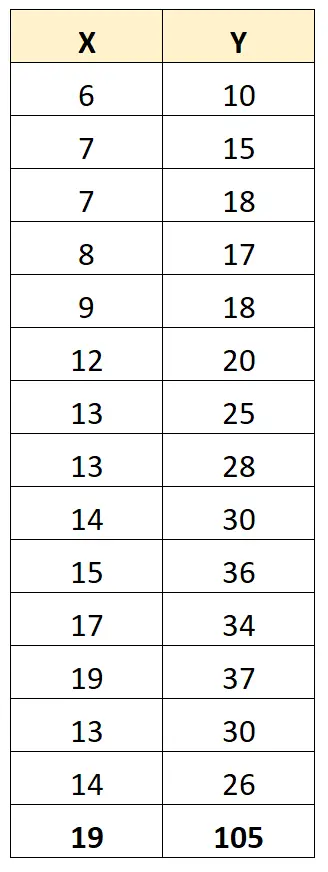
Koefisien korelasi Pearson antara X dan Y sekarang adalah 0,711 .
Pencilan secara signifikan mengubah koefisien korelasi Pearson antara kedua variabel. Dalam hal ini, mungkin masuk akal untuk menghapus outlier dari kumpulan data.
Terkait: Panduan Lengkap: Kapan Menghapus Pencilan dalam Data
Sumber daya tambahan
Tutorial berikut memberikan informasi tambahan tentang korelasi Pearson:
Pengantar Koefisien Korelasi Pearson
Cara melaporkan korelasi Pearson dalam format APA
Cara Menghitung Koefisien Korelasi Pearson Secara Manual