Panduan lengkap: cara mengecek asumsi manova

MANOVA (analisis varians multivariat) digunakan untuk menganalisis bagaimana satu atau lebih variabel faktor mempengaruhi beberapa variabel respons.

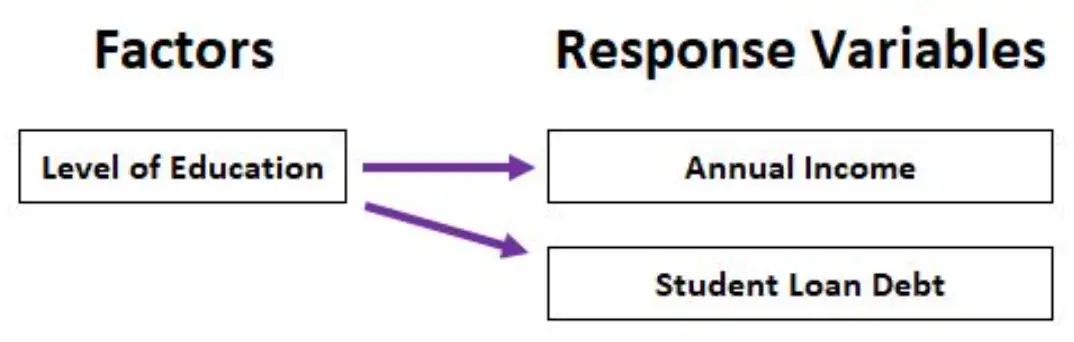
Misalnya, kita dapat menggunakan MANOVA untuk menganalisis bagaimana tingkat pendidikan (ijazah sekolah menengah atas, gelar associate, gelar sarjana, gelar master) mempengaruhi pendapatan tahunan dan total utang pinjaman mahasiswa.

Terkait: Perbedaan ANOVA, ANCOVA, MANOVA dan MANCOVA

Setiap kali kita melakukan MANOVA, kita harus memverifikasi bahwa asumsi berikut terpenuhi:

1. Normalitas multivariat – Variabel respons multivariat terdistribusi normal dalam setiap kelompok variabel faktor.

2. Independensi – Setiap observasi diambil sampelnya secara acak dan independen dari populasi.

3. Varians yang sama – Matriks kovarians populasi setiap kelompok adalah sama.

4. Tidak ada outlier multivariat – Tidak ada outlier multivariat yang ekstrim.

Pada artikel ini kami memberikan penjelasan masing-masing asumsi serta cara menentukan apakah asumsi tersebut terpenuhi.

Asumsi 1: Normalitas multivariat

MANOVA mengasumsikan bahwa variabel respons multivariat terdistribusi normal dalam setiap kelompok variabel faktor.

Jika terdapat minimal 20 observasi untuk setiap kombinasi faktor*variabel respon, maka asumsi normalitas multivariat dapat diasumsikan terpenuhi.

Jika terdapat kurang dari 20 observasi untuk setiap kombinasi faktor*variabel respons, kita dapat membuat matriks scatterplot untuk memvisualisasikan residu dan memeriksa secara visual apakah asumsi ini terpenuhi.

Untungnya, MANOVA diketahui kuat terhadap penyimpangan dari normalitas multivariat, sehingga penyimpangan kecil hingga sedang umumnya tidak menjadi masalah.

Hipotesis 2: Kemandirian

MANOVA mengasumsikan bahwa setiap observasi diambil sampelnya secara acak dan independen dari populasi.

Selama metode pengambilan sampel probabilitas (setiap anggota populasi mempunyai probabilitas yang sama untuk terpilih menjadi sampel) digunakan untuk mengumpulkan data, kita dapat berasumsi bahwa setiap observasi diambil sampelnya secara acak dan independen.

Contoh metode pengambilan sampel probabilitas meliputi:

• Contoh acak sederhana
• Pengambilan sampel acak bertingkat
• Pengambilan sampel cluster acak
• Pengambilan sampel acak sistematis

Asumsi 3: varians yang sama

MANOVA mengasumsikan bahwa matriks kovarians populasi setiap kelompok adalah sama.

Cara paling umum untuk menguji hipotesis ini adalah dengan menggunakan uji M Box. Pengujian ini diketahui cukup ketat, itulah sebabnya kami biasanya menggunakan tingkat signifikansi 0,001 untuk menentukan apakah matriks kovarians populasi sama atau tidak.

Jika nilai p dari uji Box’s M lebih besar dari 0,001, kita dapat berasumsi bahwa asumsi ini terpenuhi.

Untungnya, bahkan jika nilai p tes tersebut kurang dari 0,001, MANOVA cenderung kuat terhadap penyimpangan dari hipotesis ini.

Agar matriks kovarians yang tidak sama menjadi masalah, perbedaan antara matriks kovarians harus cukup ekstrem.

Hipotesis 4: tidak ada outlier multivariat

MANOVA mengasumsikan bahwa tidak ada outlier multivariat ekstrim dalam data yang dapat mempengaruhi hasil secara signifikan.

Cara paling umum untuk memverifikasi asumsi ini adalah dengan menghitung jarak Mahalanobis untuk setiap observasi, yang mewakili jarak antara dua titik dalam ruang multivariat.

Jika nilai p yang sesuai untuk jarak pengamatan Mahalanobis kurang dari 0,001, secara umum kami menyatakan pengamatan tersebut sebagai outlier ekstrim.

Simak tutorial berikut untuk melihat cara menghitung jarak Mahalanobis di berbagai software statistik:

• Cara menghitung jarak Mahalanobis di R
• Cara Menghitung Jarak Mahalanobis di SPSS
• Cara Menghitung Jarak Mahalanobis dengan Python

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan MANOVA di berbagai software statistik:

Cara melakukan MANOVA di R
Cara Melakukan MANOVA di SPSS
Cara melakukan MANOVA di Stata