Memahami hipotesis null untuk model anova

ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.

ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (semua mean grup adalah sama)
• H _A : Setidaknya rata-rata satu kelompok berbeda   istirahat

Untuk memutuskan apakah kita harus menolak hipotesis nol atau tidak, kita perlu mengacu pada nilai p pada hasil tabel ANOVA.

Jika nilai p berada di bawah tingkat signifikansi tertentu (misalnya 0,05), maka kita dapat menolak hipotesis nol dan menyimpulkan bahwa tidak semua rata-rata kelompok adalah sama.

ANOVA dua arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen yang ditugaskan pada dua variabel (terkadang disebut “faktor”).

ANOVA dua arah menguji tiga hipotesis nol secara bersamaan:

• Semua rata-rata kelompok adalah sama pada setiap tingkat variabel pertama
• Semua rata-rata kelompok adalah sama pada setiap tingkat variabel kedua
• Tidak terdapat efek interaksi antara kedua variabel

Untuk memutuskan apakah kita harus menolak setiap hipotesis nol atau tidak, kita perlu mengacu pada nilai p pada hasil tabel ANOVA dua arah.

Contoh berikut menunjukkan cara memutuskan apakah hipotesis nol akan ditolak atau tidak dalam ANOVA satu arah dan ANOVA dua arah.

Contoh 1: ANOVA satu arah

Misalkan kita ingin mengetahui apakah tiga program persiapan ujian yang berbeda menghasilkan nilai rata-rata yang berbeda pada ujian tertentu. Untuk mengujinya, kami merekrut 30 siswa untuk berpartisipasi dalam penelitian dan membagi mereka menjadi tiga kelompok.

Siswa di setiap kelompok secara acak ditugaskan untuk menggunakan salah satu dari tiga program persiapan ujian selama tiga minggu berikutnya untuk mempersiapkan ujian. Pada akhir tiga minggu, semua siswa mengikuti ujian yang sama.

Hasil ujian masing-masing kelompok ditunjukkan di bawah ini:

Saat kita memasukkan nilai-nilai ini ke dalam kalkulator ANOVA satu arah , kita menerima tabel ANOVA berikut sebagai keluaran:

Perhatikan bahwa nilai p adalah 0,11385 .

Untuk contoh khusus ini, kami akan menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (rata-rata nilai ujian tiap kelompok adalah sama)
• H _A : Setidaknya rata-rata satu kelompok berbeda   istirahat

Karena nilai p tabel ANOVA tidak kurang dari 0,05, kami gagal menolak hipotesis nol.

Artinya, kami tidak memiliki cukup bukti untuk mengatakan bahwa terdapat perbedaan yang signifikan secara statistik antara rata-rata nilai ujian ketiga kelompok.

Contoh 2: ANOVA dua arah

Misalkan seorang ahli botani ingin mengetahui apakah pertumbuhan tanaman dipengaruhi oleh paparan sinar matahari dan frekuensi penyiraman.

Ia menanam 40 benih dan membiarkannya tumbuh selama dua bulan dalam kondisi paparan sinar matahari dan frekuensi penyiraman yang berbeda. Setelah dua bulan, dia mencatat tinggi setiap tanaman. Hasilnya ditunjukkan di bawah ini:

Pada tabel di atas kita melihat lima tanaman ditanam pada setiap kombinasi kondisi.

Misalnya, lima tanaman ditanam dengan penyiraman setiap hari dan tanpa sinar matahari dan tingginya setelah dua bulan adalah 4,8 inci, 4,4 inci, 3,2 inci, 3,9 inci, dan 4,4 inci:

Dia melakukan ANOVA dua arah di Excel dan memperoleh hasil berikut:

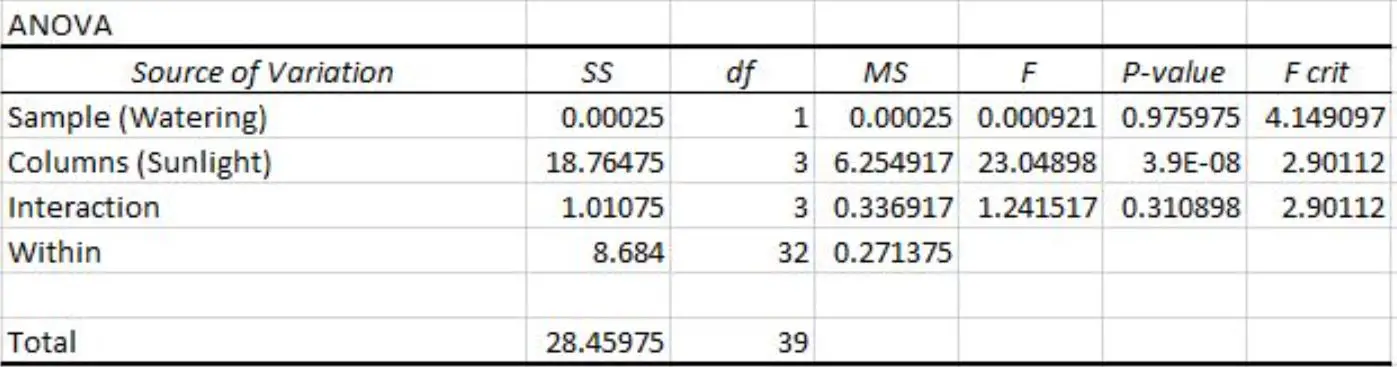
Nilai p berikut dapat kita lihat pada hasil tabel ANOVA dua arah:

• Nilai p untuk frekuensi penyiraman adalah 0,975975 . Hal ini tidak signifikan secara statistik pada tingkat signifikansi 0,05.
• Nilai p untuk paparan sinar matahari adalah 3,9E-8 (0,000000039) . Hal ini signifikan secara statistik pada tingkat signifikansi 0,05.
• Nilai p-value interaksi frekuensi penyiraman dengan paparan sinar matahari sebesar 0,310898 . Hal ini tidak signifikan secara statistik pada tingkat signifikansi 0,05.

Hasil ini menunjukkan bahwa paparan sinar matahari merupakan satu-satunya faktor yang mempunyai pengaruh signifikan secara statistik terhadap tinggi tanaman.

Dan karena tidak ada efek interaksi, maka efek paparan sinar matahari konsisten pada setiap tingkat frekuensi penyiraman.

Sederhananya, apakah tanaman disiram setiap hari atau setiap minggu tidak berdampak pada pengaruh paparan sinar matahari terhadap tanaman.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang model ANOVA:

Bagaimana menginterpretasikan nilai F dan nilai P dalam ANOVA
Cara menghitung jumlah kuadrat di ANOVA
Apa arti nilai F yang tinggi pada ANOVA?