Lima asumsi regresi linier berganda

Regresi linier berganda merupakan metode statistik yang dapat kita gunakan untuk memahami hubungan antara beberapa variabel prediktor dan variabel respon .

Namun, sebelum melakukan regresi linier berganda, pertama-tama kita harus memastikan bahwa lima asumsi terpenuhi:

1. Hubungan linier : Terdapat hubungan linier antara masing-masing variabel prediktor dengan variabel respon.

2. Tidak ada multikolinearitas: tidak ada satupun variabel prediktor yang berkorelasi tinggi satu sama lain.

3. Independensi: Pengamatan bersifat independen.

4. Homoskedastisitas: residu memiliki varian yang konstan di setiap titik model linier.

5. Normalitas multivariat: Residual model terdistribusi normal.

Jika satu atau lebih asumsi tersebut tidak terpenuhi, maka hasil regresi linier berganda mungkin tidak dapat diandalkan.

Pada artikel ini kami memberikan penjelasan untuk setiap asumsi, cara menentukan asumsi terpenuhi, dan apa yang harus dilakukan jika asumsi tidak terpenuhi.

Hipotesis 1: Hubungan linier

Regresi linier berganda mengasumsikan adanya hubungan linier antara setiap variabel prediktor dan variabel respon.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk menentukan apakah asumsi ini terpenuhi adalah dengan membuat plot sebar dari setiap variabel prediktor dan variabel respon.

Hal ini memungkinkan Anda melihat secara visual apakah ada hubungan linier antara kedua variabel.

Jika titik-titik pada diagram sebar terletak kira-kira sepanjang garis diagonal lurus, kemungkinan besar terdapat hubungan linier antar variabel.

Misalnya, titik-titik pada grafik di bawah tampak terletak pada garis lurus, yang menunjukkan bahwa terdapat hubungan linier antara variabel prediktor tertentu (x) dan variabel respons (y):

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika tidak ada hubungan linier antara satu atau lebih variabel prediktor dan variabel respon, maka kita mempunyai beberapa pilihan:

1. Terapkan transformasi nonlinier pada variabel prediktor, misalnya mengambil log atau akar kuadrat. Hal ini sering kali dapat mengubah hubungan menjadi lebih linier.

2. Tambahkan variabel prediktor lain ke dalam model. Misalnya, jika plot x versus y berbentuk parabola, maka masuk akal untuk menambahkan X ² sebagai variabel prediktor tambahan dalam model.

3. Hapus variabel prediktor dari model. Dalam kasus yang paling ekstrim, jika tidak ada hubungan linier antara variabel prediktor tertentu dan variabel respon, maka tidak ada gunanya memasukkan variabel prediktor ke dalam model.

Hipotesis 2: tidak ada multikolinearitas

Regresi linier berganda mengasumsikan bahwa tidak ada satu pun variabel prediktor yang berkorelasi tinggi satu sama lain.

Ketika satu atau lebih variabel prediktor berkorelasi tinggi, model regresi mengalami multikolinearitas , sehingga estimasi koefisien model tidak dapat diandalkan.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk mengetahui terpenuhinya asumsi tersebut adalah dengan menghitung nilai VIF setiap variabel prediktor.

Nilai VIF dimulai dari 1 dan tidak memiliki batas atas. Umumnya nilai VIF di atas 5* menunjukkan potensi multikolinearitas.

Tutorial berikut menunjukkan cara menghitung VIF di berbagai software statistik:

• Cara menghitung VIF di R
• Cara menghitung VIF dengan Python
• Cara menghitung VIF di excel

*Terkadang peneliti menggunakan nilai VIF 10, bergantung pada bidang studinya.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika satu atau lebih variabel prediktor memiliki nilai VIF lebih besar dari 5, cara termudah untuk mengatasi masalah ini adalah dengan menghapus variabel prediktor yang memiliki nilai VIF tinggi.

Alternatifnya, jika Anda ingin mempertahankan setiap variabel prediktor dalam model, Anda dapat menggunakan metode statistik yang berbeda, seperti regresi ridge , regresi laso , atau regresi kuadrat terkecil parsial , yang dirancang untuk menangani variabel prediktor yang berkorelasi tinggi.

Hipotesis 3: Kemandirian

Regresi linier berganda mengasumsikan bahwa setiap observasi dalam kumpulan data bersifat independen.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara paling sederhana untuk menentukan apakah asumsi ini terpenuhi adalah dengan melakukan uji Durbin-Watson , yang merupakan uji statistik formal yang memberi tahu kita apakah residu (dan observasi) menunjukkan autokorelasi atau tidak.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Bergantung pada bagaimana asumsi ini dilanggar, Anda memiliki beberapa pilihan:

• Untuk korelasi serial positif, pertimbangkan untuk menambahkan lag variabel dependen dan/atau independen ke dalam model.
• Untuk korelasi serial negatif, pastikan tidak ada variabel yang mengalami over-delayed .
• Untuk korelasi musiman, pertimbangkan untuk menambahkan boneka musiman ke model.

Hipotesis 4: homoskedastisitas

Regresi linier berganda mengasumsikan bahwa residu memiliki varian yang konstan di setiap titik dalam model linier. Jika hal ini tidak terjadi, maka residunya mengalami heteroskedastisitas .

Jika terdapat heteroskedastisitas dalam analisis regresi, maka hasil model regresi menjadi tidak dapat diandalkan.

Secara khusus, heteroskedastisitas meningkatkan varians estimasi koefisien regresi, namun model regresi tidak memperhitungkannya. Hal ini membuat model regresi lebih mungkin mengklaim bahwa suatu istilah dalam model tersebut signifikan secara statistik, padahal kenyataannya tidak.

Bagaimana menentukan apakah asumsi ini terpenuhi

Cara termudah untuk menentukan apakah asumsi ini terpenuhi adalah dengan membuat plot residu terstandar terhadap nilai prediksi.

Setelah Anda menyesuaikan model regresi ke kumpulan data, Anda dapat membuat plot sebar yang menampilkan nilai prediksi variabel respons pada sumbu x dan residu standar model pada sumbu x. kamu.

Jika titik-titik pada diagram sebar menunjukkan tren, maka terjadi heteroskedastisitas.

Bagan berikut menunjukkan contoh model regresi dimana heteroskedastisitas tidak menjadi masalah:

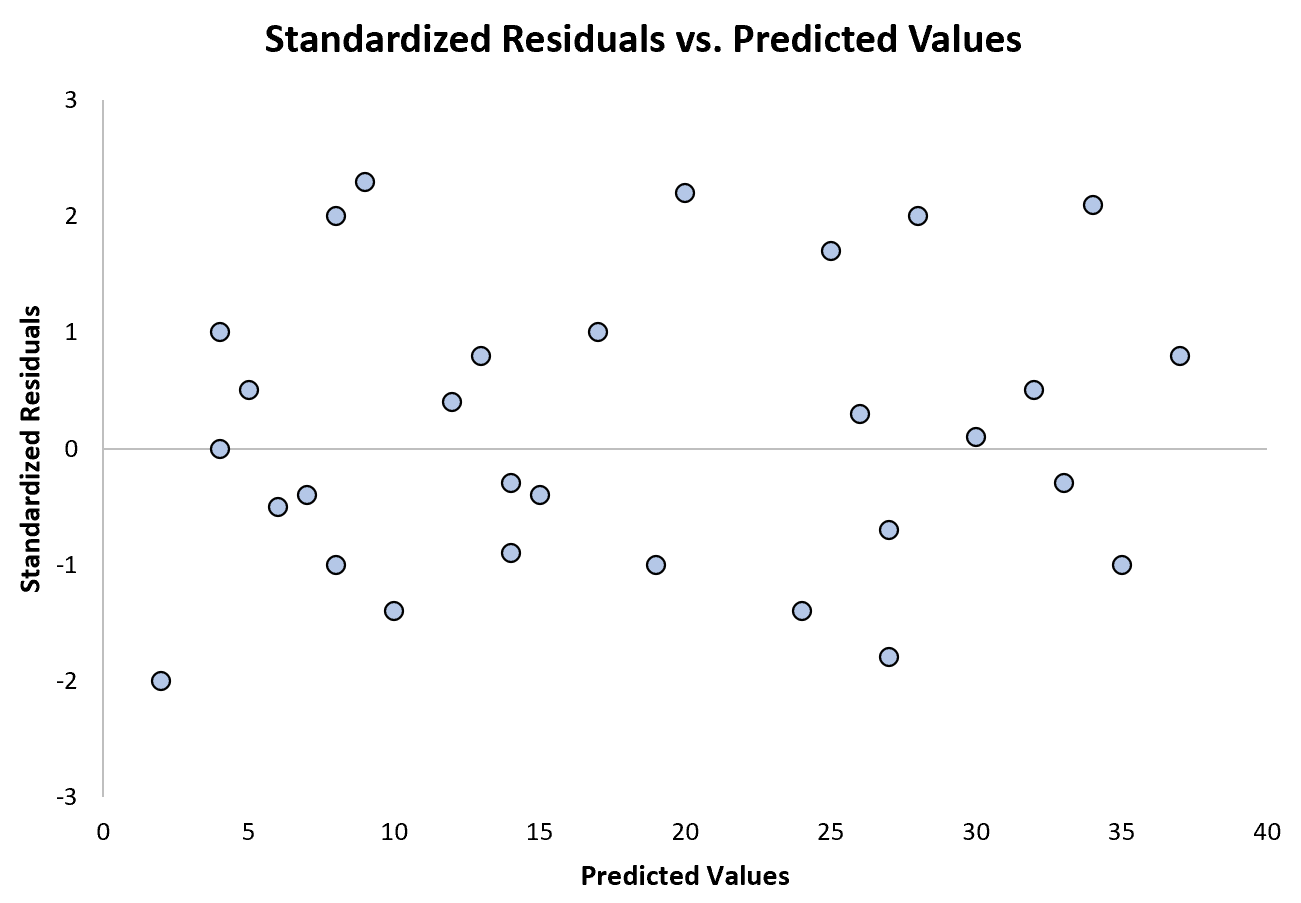
Perhatikan bahwa residu terstandar tersebar di sekitar nol tanpa pola yang jelas.

Bagan berikut menunjukkan contoh model regresi dimana heteroskedastisitas menjadi masalah:

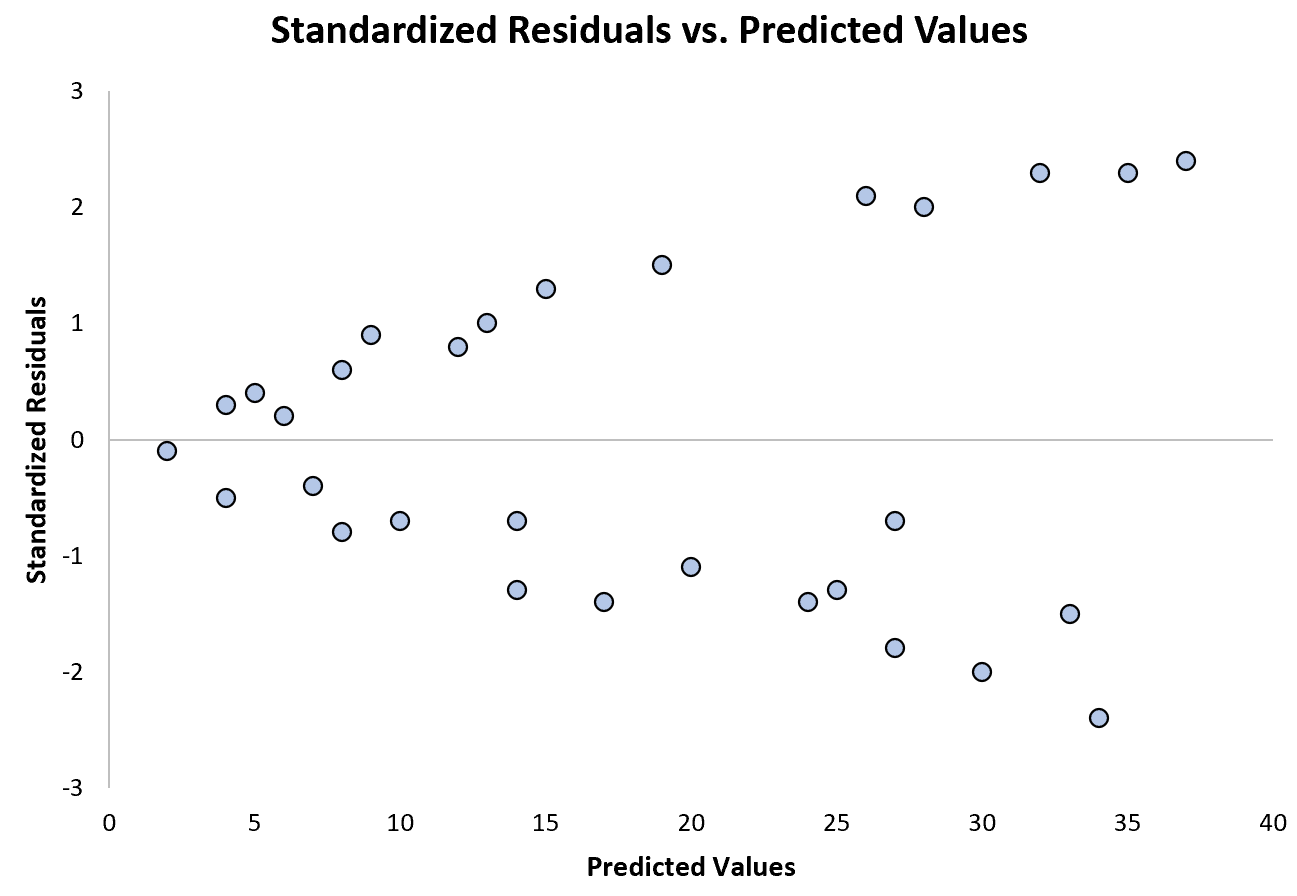
Perhatikan bagaimana residu terstandarisasi semakin menyebar seiring dengan meningkatnya nilai prediksi. Bentuk “kerucut” ini merupakan tanda klasik heteroskedastisitas:

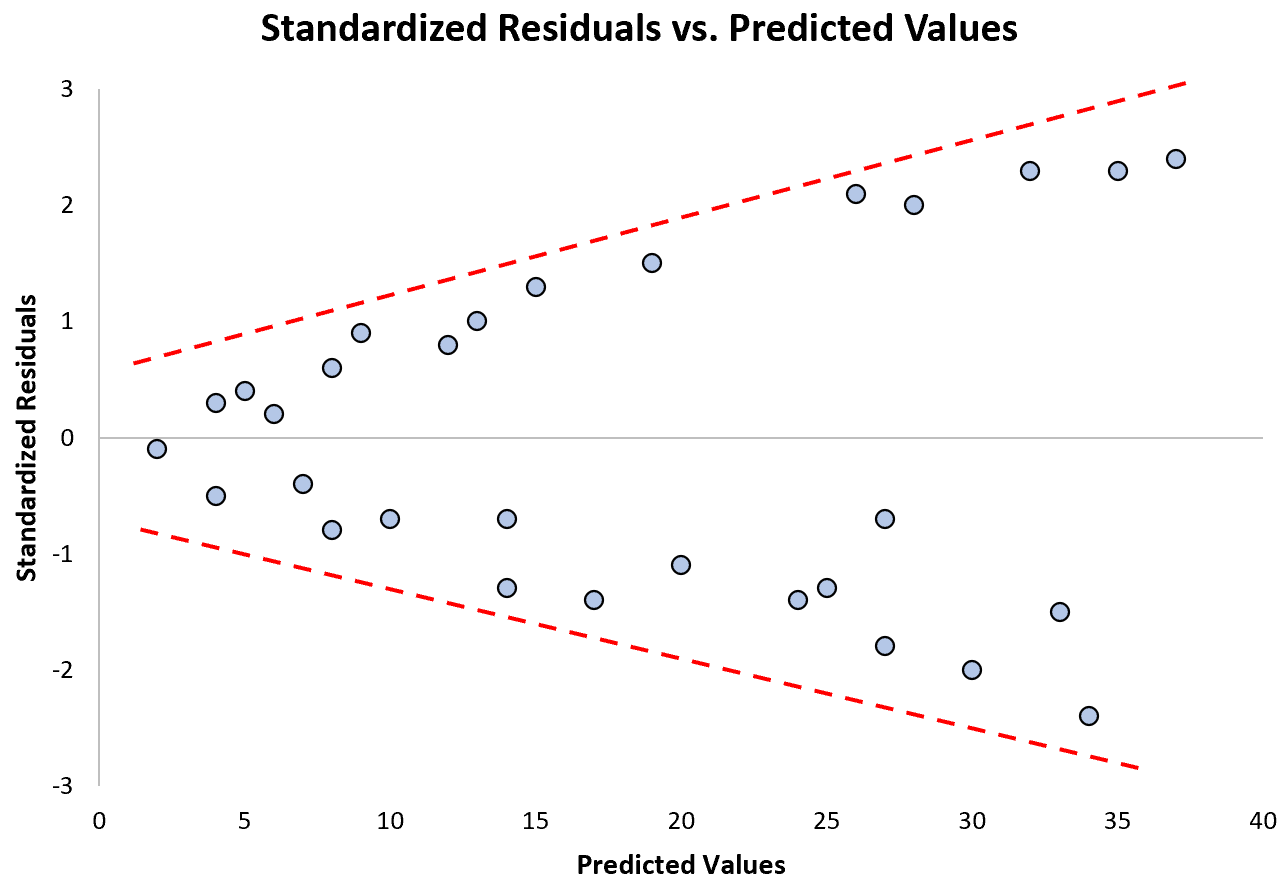
Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Ada tiga cara umum untuk mengoreksi heteroskedastisitas:

1. Transformasikan variabel respon. Cara paling umum untuk mengatasi heteroskedastisitas adalah dengan mentransformasikan variabel respon dengan mengambil log, akar kuadrat, atau akar pangkat tiga dari seluruh nilai variabel respon. Hal ini seringkali mengakibatkan hilangnya heteroskedastisitas.

2. Definisikan kembali variabel respon. Salah satu cara untuk mendefinisikan ulang variabel respons adalah dengan menggunakan laju , bukan nilai mentah. Misalnya, daripada menggunakan ukuran populasi untuk memprediksi jumlah toko bunga di suatu kota, kita dapat menggunakan ukuran populasi untuk memprediksi jumlah toko bunga per kapita.

Dalam kebanyakan kasus, hal ini mengurangi variabilitas yang secara alami terjadi dalam populasi yang lebih besar karena kita mengukur jumlah toko bunga per orang, bukan jumlah toko bunga itu sendiri.

3. Gunakan regresi tertimbang. Cara lain untuk mengoreksi heteroskedastisitas adalah dengan menggunakan regresi berbobot, yang memberikan bobot pada setiap titik data berdasarkan varian nilai yang dipasang.

Pada dasarnya, hal ini memberikan bobot rendah pada titik data yang memiliki varian lebih tinggi, sehingga mengurangi kuadrat residunya. Apabila bobot yang digunakan sesuai maka masalah heteroskedastisitas dapat dihilangkan.

Terkait : Cara Melakukan Regresi Tertimbang di R

Asumsi 4: Normalitas multivariat

Regresi linier berganda mengasumsikan bahwa residu model terdistribusi normal.

Bagaimana menentukan apakah asumsi ini terpenuhi

Ada dua cara umum untuk memeriksa apakah asumsi ini terpenuhi:

1. Verifikasi hipotesis secara visual menggunakan plot QQ .

Plot QQ, kependekan dari plot kuantil-kuantil, adalah jenis plot yang dapat kita gunakan untuk menentukan apakah residu suatu model mengikuti distribusi normal atau tidak. Jika titik-titik pada plot kira-kira membentuk garis lurus diagonal, maka asumsi normalitas terpenuhi.

Plot QQ berikut menunjukkan contoh residu yang kira-kira mengikuti distribusi normal:

Namun, plot QQ di bawah ini menunjukkan contoh kasus di mana residu jelas-jelas menyimpang dari garis lurus diagonal, yang menunjukkan bahwa residu tersebut tidak mengikuti distribusi normal:

2. Verifikasi hipotesis menggunakan uji statistik formal seperti Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre, atau D’Agostino-Pearson.

Ingatlah bahwa pengujian ini sensitif terhadap ukuran sampel yang besar – artinya, pengujian ini sering kali menyimpulkan bahwa residu tidak normal jika ukuran sampel Anda sangat besar. Inilah sebabnya mengapa seringkali lebih mudah menggunakan metode grafis seperti plot QQ untuk memverifikasi hipotesis ini.

Apa yang harus dilakukan jika asumsi ini tidak dipatuhi

Jika asumsi normalitas tidak terpenuhi, Anda memiliki beberapa pilihan:

1. Pertama, periksa apakah tidak terdapat outlier ekstrim pada data yang mengakibatkan pelanggaran asumsi normalitas.

2. Kemudian Anda dapat menerapkan transformasi nonlinier pada variabel respon, misalnya dengan mengambil akar kuadrat, log, atau akar pangkat tiga dari seluruh nilai variabel respon. Hal ini sering kali menghasilkan distribusi residu model yang lebih normal.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang regresi linier berganda dan asumsinya:

Pengantar Regresi Linier Berganda
Panduan Heteroskedastisitas dalam Analisis Regresi
Panduan Multikolinearitas dan VIF dalam Regresi

Tutorial berikut memberikan contoh langkah demi langkah tentang cara melakukan regresi linier berganda menggunakan perangkat lunak statistik yang berbeda:

Cara melakukan regresi linier berganda di Excel
Cara melakukan regresi linier berganda di R
Cara melakukan regresi linier berganda di SPSS
Cara melakukan regresi linier berganda di Stata