Cara menghitung nilai p di excel (3 contoh)

Dalam statistik, kami menggunakan pengujian hipotesis untuk menentukan apakah pernyataan tentang suatu parameter populasi benar atau tidak.

Saat kita melakukan uji hipotesis, kita sering diberikan statistik uji T-score.

Setelah kami menemukan statistik uji skor-t ini, kami kemudian dapat menemukan nilai p yang terkait dengannya.

Jika nilai p ini lebih kecil dari nilai tertentu (misalnya 0,10, 0,05, 0,01), maka kami menolak hipotesis nol pengujian tersebut dan menyimpulkan bahwa hasil kami signifikan secara statistik.

Contoh berikut memperlihatkan cara menghitung nilai p untuk statistik pengujian di Excel dalam tiga skenario berbeda.

Contoh 1: Hitung nilai P untuk pengujian dua sisi

Misalkan seorang ahli botani ingin mengetahui apakah tinggi rata-rata suatu spesies tumbuhan tertentu sama dengan 15 inci.

Dalam sampel acak 12 tanaman, ia menemukan bahwa rata-rata tinggi sampel adalah 14,33 inci dan simpangan baku sampel adalah 1,37 inci.

Ia melakukan uji hipotesis menggunakan hipotesis nol dan alternatif berikut:

H ₀ (hipotesis nol): μ= 15 inci

H _A (hipotesis alternatif): μ ≠ 15 inci

Statistik uji dihitung sebagai berikut:

• t = ( X – µ) / (s/ √n )
• t = (14.33-15) / (1.37/√ 12 )
• t = -1,694

Derajat kebebasan yang terkait dengan statistik pengujian ini adalah n-1 = 12-1 = 11 .

Untuk mencari nilai p untuk statistik pengujian ini, kita akan menggunakan rumus berikut di Excel:

 =T.DIST.2T(ABS(-1.694), 11)

Tangkapan layar berikut menunjukkan cara menggunakan rumus ini dalam praktik.

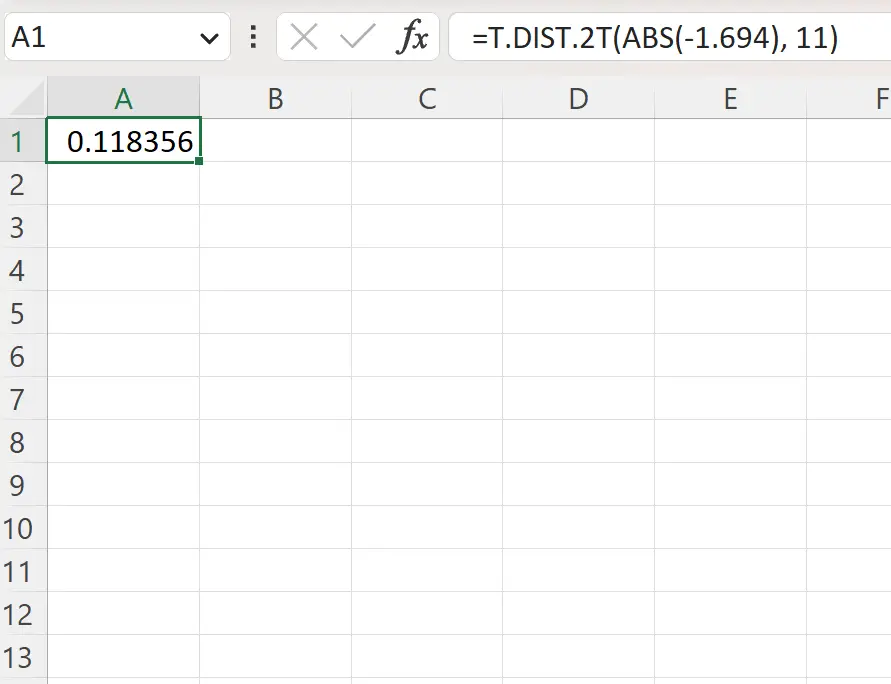
Nilai p dua sisi adalah 0,1184 .

Sejak nilai ini tidak kurang dari 0,05, kita gagal menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa rata-rata tinggi tanaman berbeda dari 15 inci.

Contoh 2: Hitung nilai P untuk tes di sebelah kiri

Misalkan kita asumsikan berat rata-rata sebuah gadget tertentu yang diproduksi di sebuah pabrik adalah 20 gram. Namun, seorang pemeriksa memperkirakan berat rata-rata sebenarnya kurang dari 20 gram.

Untuk mengujinya, ia menimbang sampel acak sederhana yang terdiri dari 20 widget dan mendapatkan informasi berikut:

• n = 20 widget
• x = 19,8 gram
• s = 3,1 gram

Ia kemudian melakukan uji hipotesis menggunakan hipotesis nol dan hipotesis alternatif berikut:

H ₀ (hipotesis nol): μ ≥ 20 gram

H _A (hipotesis alternatif): μ < 20 gram

Statistik uji dihitung sebagai berikut:

• t = ( X – µ) / (s/ √n )
• t = (19,8-20) / (3,1/√ 20 )
• t = -.2885

Derajat kebebasan yang terkait dengan statistik pengujian ini adalah n-1 = 20-1 = 19 .

Untuk mencari nilai p untuk statistik pengujian ini, kita akan menggunakan rumus berikut di Excel:

 =T.DIST(-.2885, 19, TRUE)

Tangkapan layar berikut menunjukkan cara menggunakan rumus ini dalam praktik.

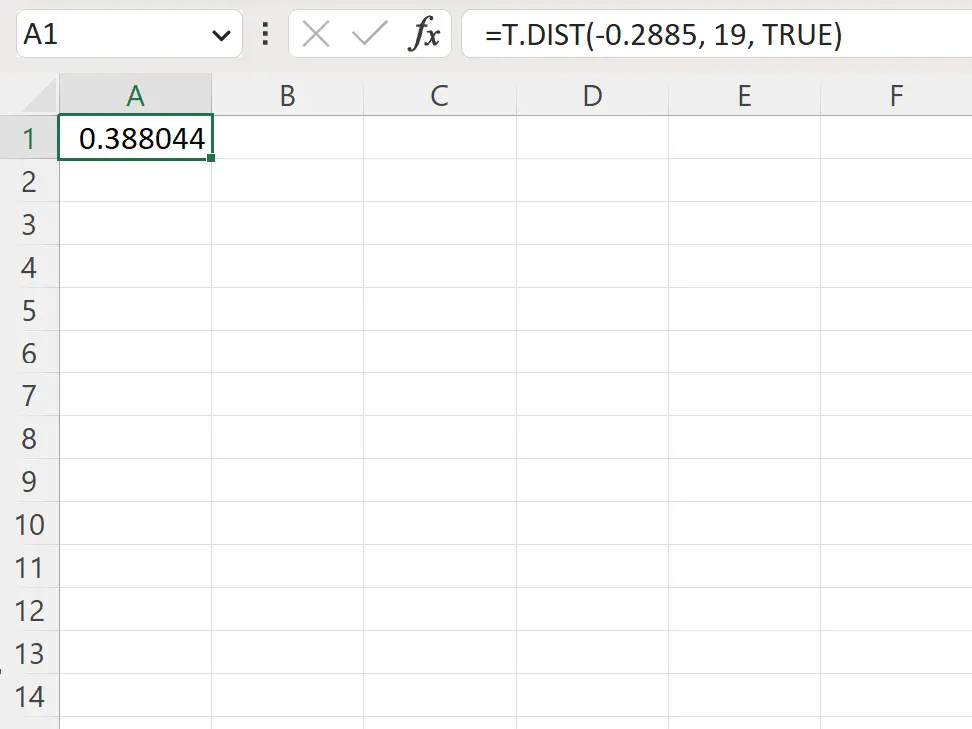
Nilai p di sebelah kiri adalah 0,388044 .

Sejak nilai ini tidak kurang dari 0,05, maka pemeriksa gagal menolak hipotesis nol. Tidak ada cukup bukti yang menyatakan bahwa berat rata-rata sebenarnya widget yang diproduksi di pabrik ini kurang dari 20 gram.

Catatan : Kami menggunakan argumen TRUE untuk menentukan bahwa fungsi distribusi kumulatif harus digunakan saat menghitung nilai p.

Contoh 3: Hitung nilai P untuk uji sisi kanan

Misalkan tinggi rata-rata suatu spesies tumbuhan tertentu adalah 10 inci. Namun, seorang ahli botani mengatakan tinggi rata-rata sebenarnya lebih dari 10 inci.

Untuk menguji klaim ini, dia mengukur tinggi sampel acak sederhana yang terdiri dari 15 tanaman dan memperoleh informasi berikut:

• n = 15 tanaman
• x = 11,4 inci
• s = 2,5 inci

Ia kemudian melakukan uji hipotesis menggunakan hipotesis nol dan hipotesis alternatif berikut:

H ₀ (hipotesis nol): μ ≤ 10 inci

H _A (hipotesis alternatif): μ > 10 inci

Statistik uji dihitung sebagai berikut:

• t = ( X – µ) / (s/ √n )
• t = (11,4-10) / (2,5/√ 15 )
• t = 2,1689

Derajat kebebasan yang terkait dengan statistik pengujian ini adalah n-1 = 15-1 = 14 .

Untuk mencari nilai p untuk statistik pengujian ini, kita akan menggunakan rumus berikut di Excel:

 =T.DIST.RT(2.1689, 14)

Tangkapan layar berikut menunjukkan cara menggunakan rumus ini dalam praktik.

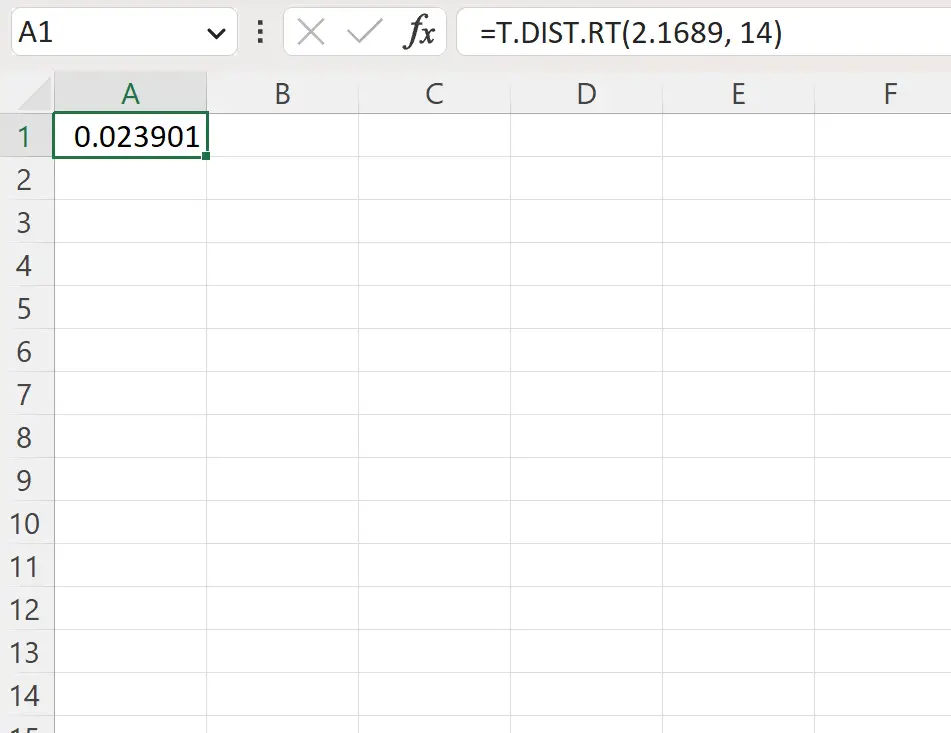
Nilai p di sebelah kanan adalah 0,023901 .

Nilai ini kurang dari 0,05, ahli botani dapat menolak hipotesis nol. Dia memiliki cukup bukti untuk mengatakan bahwa tinggi rata-rata sebenarnya dari spesies tanaman ini adalah lebih dari 10 inci.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di Excel:

Cara Menemukan Nilai P dari Z Score di Excel
Cara mencari nilai P dari statistik F di Excel
Cara mencari nilai P statistik chi-kuadrat di Excel