Distribusi pareto
Artikel ini menjelaskan apa itu distribusi Pareto dalam statistik dan kegunaannya. Anda juga akan dapat melihat grafik distribusi Pareto dan properti dari jenis distribusi probabilitas ini.
Apa itu distribusi Pareto?
Distribusi Pareto adalah distribusi probabilitas kontinu yang digunakan dalam statistik untuk memodelkan prinsip Pareto. Oleh karena itu, distribusi Pareto merupakan distribusi probabilitas yang memiliki beberapa nilai yang probabilitas terjadinya jauh lebih tinggi dibandingkan nilai lainnya.
Ingatlah bahwa hukum Pareto, disebut juga aturan 80-20, adalah prinsip statistik yang menyatakan bahwa sebagian besar penyebab suatu fenomena disebabkan oleh sebagian kecil populasi.
Distribusi Pareto mempunyai dua parameter karakteristik: parameter skala x m dan parameter bentuk α.
![]()
Awalnya, distribusi Pareto digunakan untuk menggambarkan distribusi kekayaan dalam suatu populasi, karena sebagian besar disebabkan oleh sebagian kecil populasi. Namun saat ini Distribusi Pareto mempunyai banyak penerapan, misalnya dalam pengendalian kualitas, di bidang ekonomi, di bidang sains, di bidang sosial, dll.
Nama distribusi Pareto diambil dari nama ekonom Vilfredo Pareto yang merumuskan distribusi tersebut. Namun, dia terkenal karena grafik Pareto.
Tabel distribusi Pareto
Sekarang setelah kita mengetahui definisi distribusi Pareto, mari kita lihat beberapa contoh distribusi Pareto yang direpresentasikan secara grafis.
Nah, di bawah ini Anda dapat melihat seperti apa grafik fungsi kepadatan distribusi Pareto tergantung pada nilai karakteristiknya:
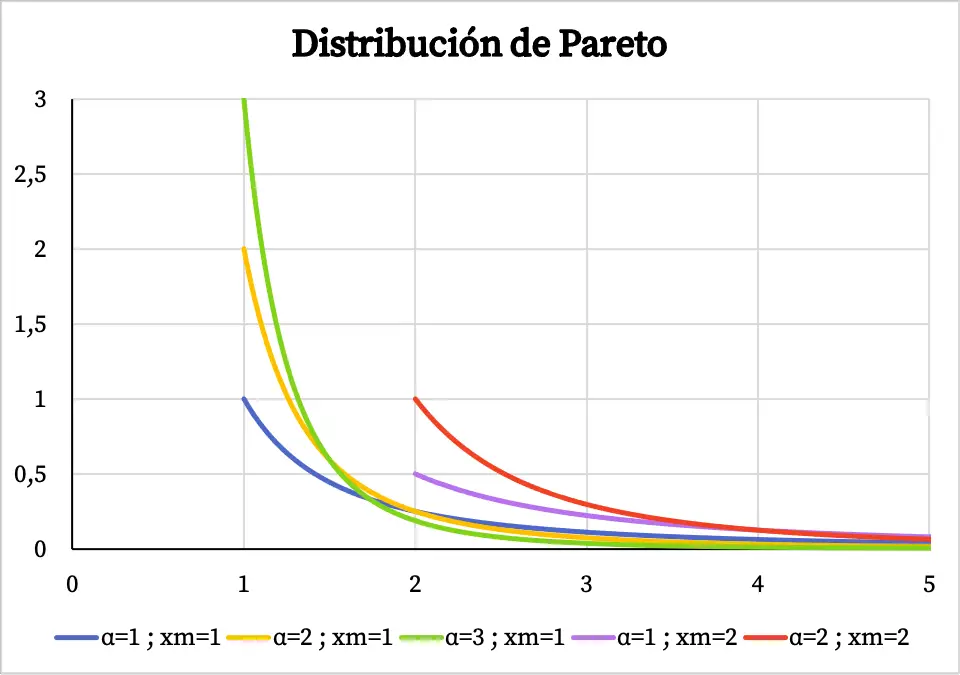
Perhatikan bahwa domain distribusi Pareto berubah dari nilai x m menjadi +∞, itulah sebabnya fungsi kepadatan tidak ada sebelum nilai x m .
Sedangkan grafik fungsi probabilitas kumulatif dari distribusi Pareto adalah sebagai berikut:
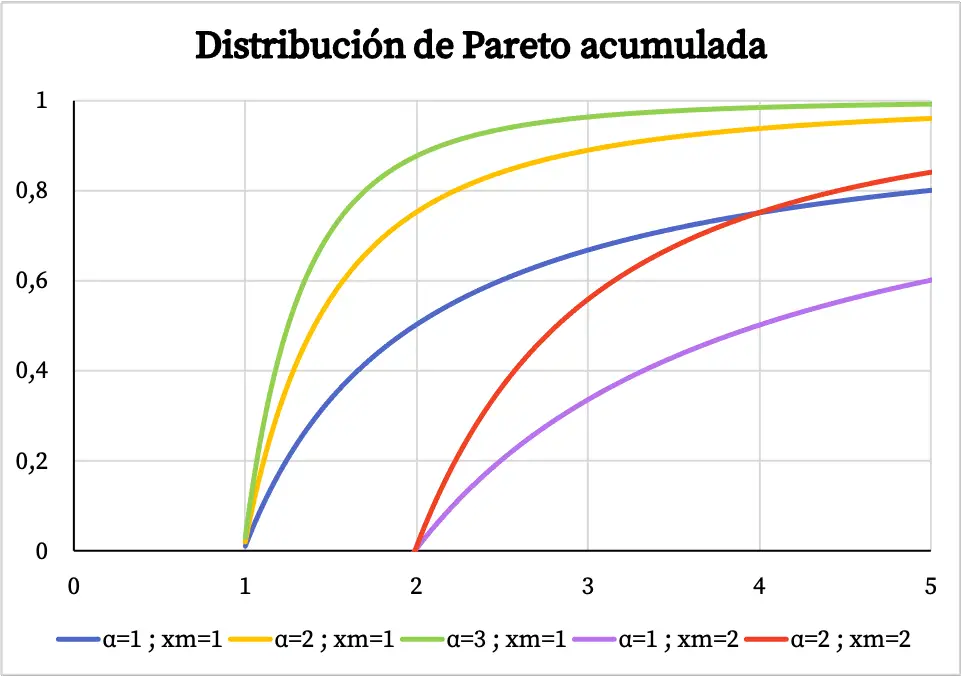
Ciri-ciri Distribusi Pareto
Di bawah ini adalah karakteristik terpenting dari distribusi Pareto terkait teori probabilitas dan statistik.
- Distribusi Pareto mempunyai dua parameter karakteristik yang menentukan kurvanya: parameter skala x m dan parameter bentuk α.
![]()
- Domain distribusi Pareto terdiri dari semua bilangan real dari parameter skala hingga plus tak terhingga.
![]()
- Jika α lebih besar dari 1, rata-rata distribusi Pareto sama dengan hasil kali α kali x m dan α dikurangi 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”34″ width=”214″ style=”vertical-align: -12px;”></p>
</p>
<ul>
<li> Varians distribusi Pareto bergantung pada dua parameter karakteristik distribusi dan dihitung dengan rumus berikut:</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png)
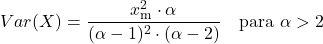
![]()
- Modus distribusi Pareto setara dengan parameter skala distribusi xm .
![]()
- Rumus fungsi kepadatan distribusi Pareto adalah:
![]()
- Demikian pula rumus fungsi probabilitas kumulatif dari distribusi Pareto adalah:
![]()
- Koefisien asimetri distribusi Pareto hanya bergantung pada parameter bentuk α dan ekspresinya adalah:
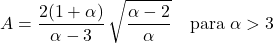
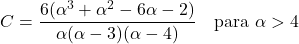
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya