Distribusi poisson atau distribusi normal: apa bedanya?

Distribusi Poisson dan distribusi normal adalah dua distribusi probabilitas yang paling umum digunakan dalam statistik.

Tutorial ini memberikan penjelasan singkat tentang setiap distribusi serta dua perbedaan utama antara distribusi tersebut.

Gambaran umum: distribusi Poisson

Distribusi Poisson menggambarkan probabilitas diperolehnya k keberhasilan selama selang waktu tertentu.

Jika suatu variabel acak X mengikuti distribusi Poisson, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = λ ^k * e ^{– λ} / k!

Emas:

• λ: jumlah rata-rata keberhasilan yang terjadi selama interval tertentu
• k: jumlah keberhasilan
• e: konstanta sama dengan sekitar 2,71828

Misalnya, sebuah rumah sakit tertentu mengalami rata-rata 2 kelahiran per jam. Kita dapat menggunakan rumus di atas untuk menentukan peluang mengalami 3 kelahiran dalam satu jam tertentu:

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0,1805

Peluang mengalami 3 kelahiran dalam satu jam tertentu adalah 0,1805 .

Gambaran umum: distribusi normal

Distribusi normal menggambarkan probabilitas suatu variabel acak mengambil nilai dalam interval tertentu.

Fungsi kepadatan probabilitas dari distribusi normal dapat ditulis sebagai:

P(X=x) = (1/σ√ 2π )e ^{-1/2((x-μ)/σ) 2}

Emas:

• σ : Simpangan baku distribusi
• μ: Rata-rata distribusi
• x: nilai variabel acak

Misalnya, berat spesies berang-berang tertentu berdistribusi normal dengan μ = 40 pon dan σ = 5 pon.

Jika kita memilih berang-berang secara acak dari populasi ini, kita dapat menggunakan rumus berikut untuk mencari probabilitas beratnya antara 38 dan 42 pon:

P ( ^{38 < /5) 2} = 0,3108

Peluang terambilnya berang-berang yang dipilih secara acak memiliki berat antara 38 dan 42 pon adalah 0,3108 .

Perbedaan #1: Bijaksana vs. Data Berkelanjutan

Perbedaan pertama antara distribusi Poisson dan distribusi normal adalah jenis data yang dimodelkan oleh masing-masing distribusi probabilitas.

Distribusi Poisson digunakan ketika bekerja dengan data diskrit yang hanya dapat mengambil nilai integer sama dengan atau lebih besar dari nol. Berikut beberapa contohnya:

• Jumlah panggilan yang diterima per jam di pusat panggilan
• Jumlah pelanggan per hari di sebuah restoran
• Jumlah kecelakaan mobil per bulan

Dalam setiap skenario, variabel acak hanya dapat mengambil nilai 0, 1, 2, 3, dst.

Distribusi normal digunakan ketika bekerja dengan data kontinu yang dapat mengambil nilai apa pun dari tak terhingga negatif hingga tak terhingga positif. Berikut beberapa contohnya:

• Berat hewan tertentu
• Ketinggian tanaman tertentu
• Waktu maraton wanita
• Suhu dalam Celcius

Dalam skenario ini, variabel acak dapat mengambil nilai apa pun seperti -11.3, 21.343435, 85, dll.

Perbedaan #2: bentuk distribusi

Perbedaan distribusi Poisson dan distribusi normal yang kedua terletak pada bentuk distribusinya.

Distribusi normal akan selalu berbentuk lonceng:

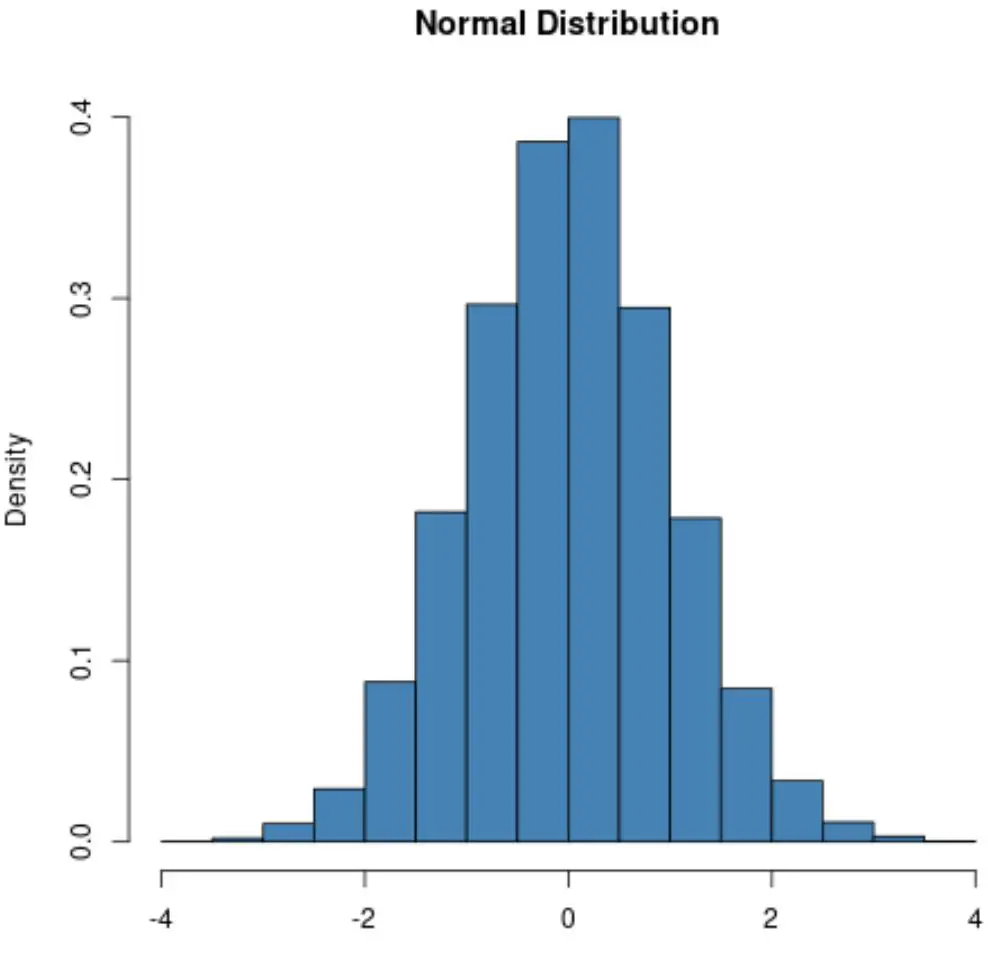
Namun bentuk distribusi Poisson bervariasi tergantung pada nilai rata-rata distribusi tersebut.

Misalnya, distribusi Poisson dengan nilai mean yang kecil seperti μ = 3 akan sangat condong ke kanan :

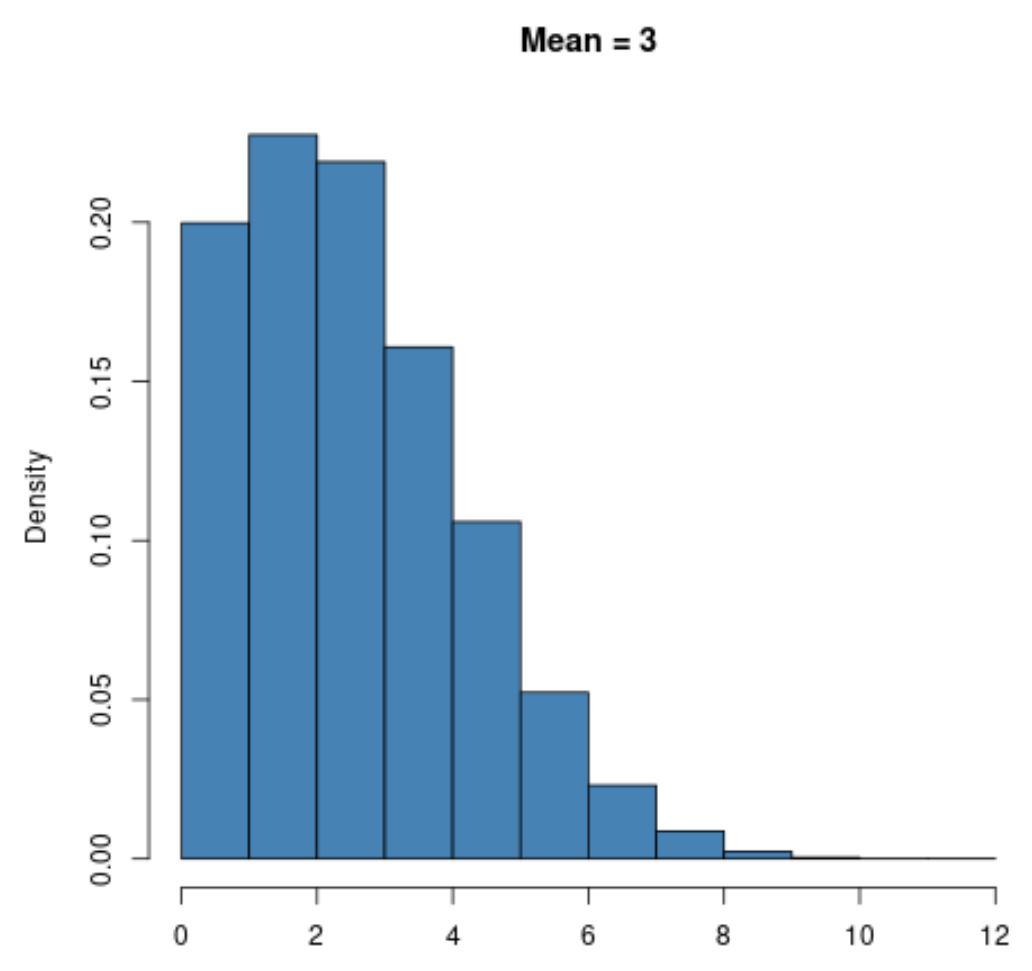
Namun distribusi Poisson dengan nilai rata-rata yang lebih besar seperti μ = 20 akan menunjukkan bentuk lonceng seperti distribusi normal:

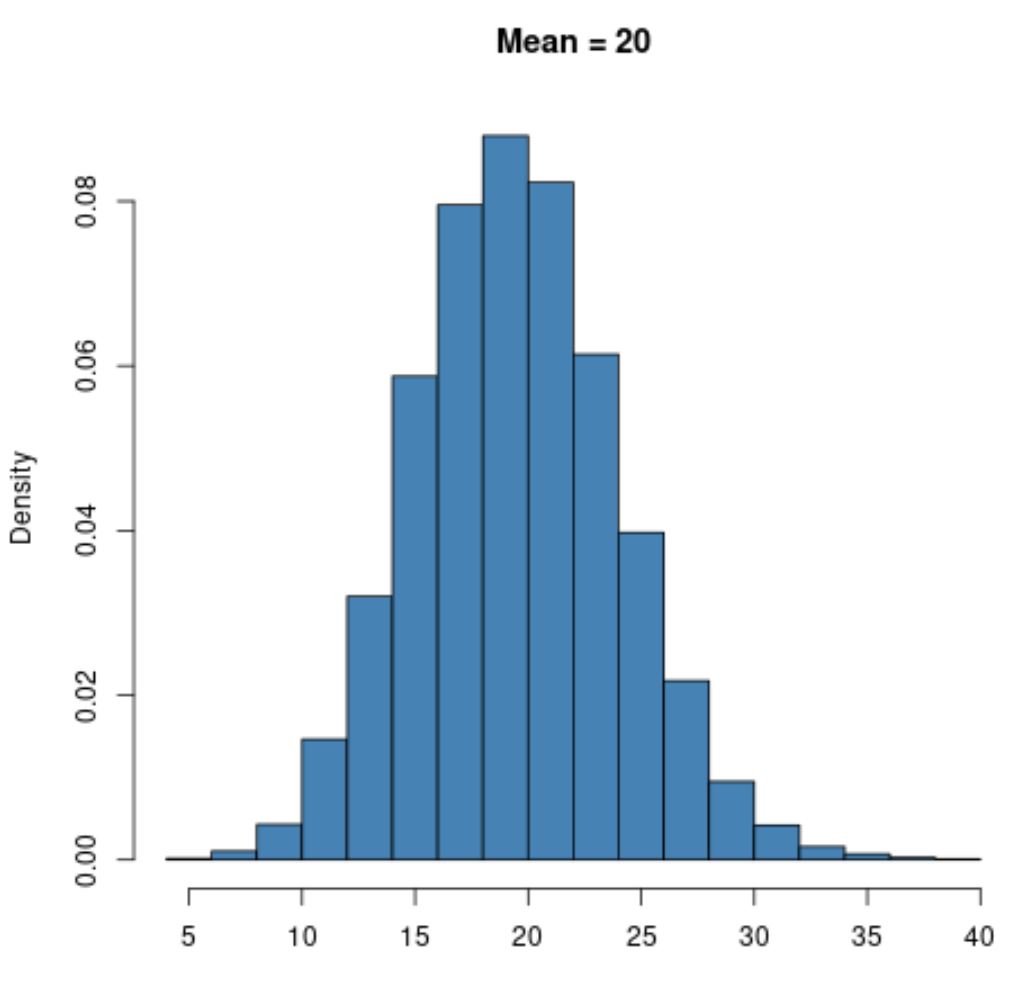
Perhatikan bahwa batas bawah distribusi Poisson akan selalu nol, berapapun nilai meannya, karena distribusi Poisson hanya dapat digunakan dengan nilai integer sama dengan atau lebih besar dari nol.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang distribusi Poisson:

Pengenalan distribusi Poisson
Empat hipotesis distribusi Poisson
5 contoh konkrit distribusi Poisson

Tutorial berikut memberikan informasi tambahan tentang distribusi normal:

Pengenalan distribusi normal
6 contoh konkrit distribusi normal
Generator Kumpulan Data Distribusi Normal