Indeks gini (atau koefisien gini)

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu indeks Gini, disebut juga koefisien Gini, dan kegunaannya. Selain itu, Anda akan menemukan latihan terpecahkan tentang cara menemukan indeks Gini. Terakhir, Anda akan dapat melihat interpretasi metrik statistik ini dan apa hubungan antara indeks Gini dan kurva Lorenz.

Apa yang dimaksud dengan indeks Gini?

Indeks Gini , disebut juga koefisien Gini , adalah nilai statistik yang digunakan untuk mengukur ketimpangan pendapatan suatu wilayah. Dengan kata lain, indeks Gini menunjukkan seberapa setara suatu wilayah dalam distribusi pendapatan antar penduduknya.

Indeks Gini adalah angka antara 0 dan 1. Jika indeks Gini bernilai 0, berarti distribusi pendapatan di suatu wilayah sudah seadil-adilnya (kesetaraan sempurna), atau dengan kata lain semua penduduk mempunyai pendapatan yang sama. Sebaliknya, jika koefisien Gini adalah 1, hal ini berarti ketimpangan sempurna, artinya satu orang mempunyai seluruh pendapatan wilayah tersebut dan orang lain tidak menerima apa pun.

Indeks Gini digunakan untuk membandingkan situasi ekonomi antara berbagai negara di dunia, karena indeks ini memungkinkan untuk membandingkan negara-negara yang paling egaliter dan, sebaliknya, negara-negara yang paling tidak setara dalam hal distribusi pendapatan.

Indeks Gini ditemukan oleh ahli statistik terkenal Corrado Gini, sesuai dengan namanya.

Cara menghitung indeks Gini

Mengingat definisi indeks Gini (atau koefisien Gini), berikut adalah cara penghitungan statistik ini.

Rumus indeks Gini (atau koefisien Gini) adalah sebagai berikut:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

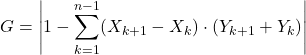
Emas:

$G$

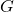
adalah indeks Gini.
$X$

adalah proporsi kumulatif dari populasi variabel.
$Y$

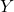
adalah proporsi kumulatif dari variabel pendapatan.

Agar Anda dapat melihat secara pasti bagaimana indeks Gini ditentukan, contoh langkah demi langkah telah diselesaikan di bawah ini:

Hitung indeks Gini penduduk yang pendapatannya ditunjukkan pada tabel berikut.

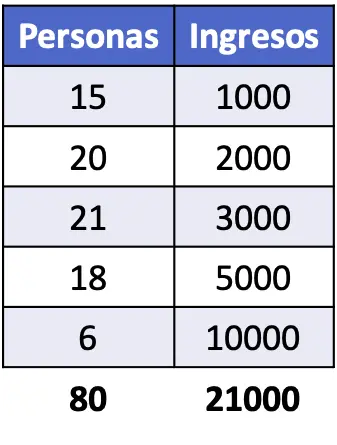
Untuk mencari koefisien Gini, kita perlu menentukan proporsi tiap tingkat pendapatan serta proporsi kumulatifnya. Selain itu, perhitungan yang diberikan dalam rumus harus dilakukan untuk mencari nilai indeks Gini.

Singkatnya, kolom berikut harus ditambahkan ke tabel data:

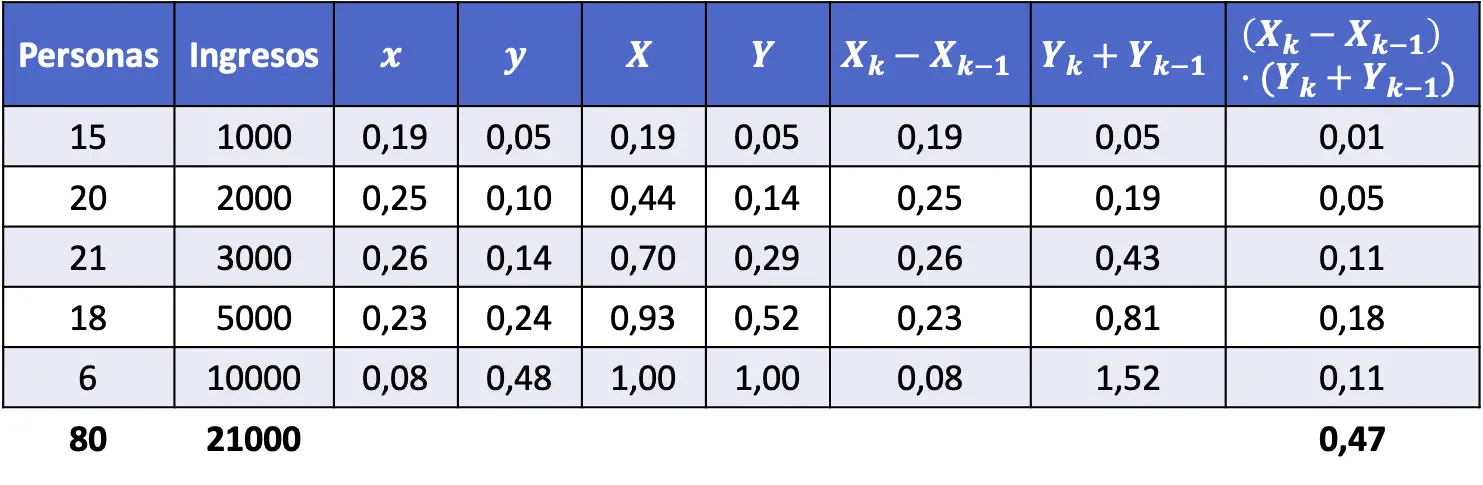
Kami sekarang menggunakan rumus indeks Gini:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

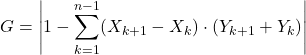
Dan terakhir, kami mengganti data ke dalam ekspresi aljabar dan menghitung koefisien Gini:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-0,47\end{vmatrix}=0,53$

Hubungan antara indeks Gini dan kurva Lorenz

Pada bagian ini, kita akan melihat bagaimana indeks Gini, juga dikenal sebagai koefisien Gini, dan kurva Lorenz saling berhubungan.

Kurva Lorenz merupakan representasi grafis dari kesenjangan ekonomi penduduk suatu wilayah. Dengan demikian, kurva Lorenz secara visual menunjukkan ketimpangan ekonomi suatu penduduk.

Di sisi lain, seperti telah kita lihat, indeks Gini adalah nilai yang digunakan untuk menggambarkan kesenjangan suatu populasi secara numerik.

Oleh karena itu, indeks Gini dan kurva Lorenz memiliki tujuan yang sama : keduanya digunakan untuk menentukan kesenjangan ekonomi antara penduduk suatu wilayah. Namun, indeks Gini mengevaluasi ketimpangan pendapatan secara numerik, sedangkan kurva Lorenz menganalisis ketimpangan ekonomi secara grafis.

Selain itu, indeks Gini dapat dihitung dari luas wilayah yang dibatasi oleh kurva Lorenz dengan rumus sebagai berikut:

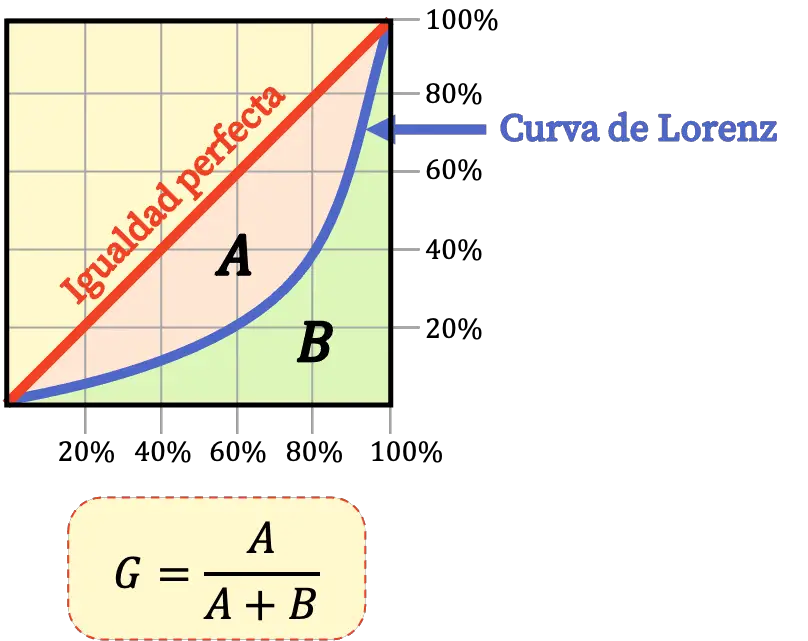
hubungan antara indeks Gini dan kurva Lorenz

Interpretasi indeks Gini

Nilai indeks Gini dapat berkisar dari 0 hingga 1, keduanya inklusif. Semakin dekat nilai koefisien Gini dengan 0, berarti semakin terjadi pemerataan ekonomi di wilayah tersebut. Sebaliknya, semakin tinggi nilai indeks Gini maka semakin besar ketimpangan distribusi pendapatan antar penduduk suatu wilayah.

Oleh karena itu, indeks Gini akan sama dengan nol dalam situasi optimal dimana semua penduduk mempunyai pendapatan yang sama persis. Sebaliknya, indeks Gini akan bernilai 1 ketika wilayah tersebut menunjukkan ketimpangan sempurna, artinya satu penduduk menerima seluruh pendapatan dan penduduk lainnya tidak mempunyai pendapatan.

Oleh karena itu, negara-negara dengan kesetaraan pendapatan lebih besar adalah negara-negara yang memiliki indeks Gini lebih rendah. Dan negara-negara yang paling tidak setara mempunyai indeks Gini yang sangat tinggi.

Seperti yang telah kita lihat, indeks Gini terkait dengan kurva Lorenz. Jadi, semakin rendah indeks Gini, maka kurva Lorenz akan semakin dekat dengan garis pemerataan sempurna. Semakin tinggi indeks Gini, semakin besar kelengkungan kurva Gini, sehingga semakin jauh jaraknya dari garis yang menunjukkan kesetaraan sempurna.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya