Interpolasi atau ekstrapolasi: apa bedanya?

Dua istilah yang sering membingungkan siswa dalam statistika adalah interpolasi dan ekstrapolasi .

Inilah perbedaannya:

Interpolasi mengacu pada nilai prediksi yang berada dalam rentang titik data.

Ekstrapolasi mengacu pada nilai prediksi yang berada di luar rentang titik data.

Contoh berikut menggambarkan perbedaan antara kedua istilah tersebut.

Contoh: interpolasi dan ekstrapolasi

Misalkan kita memiliki kumpulan data berikut:

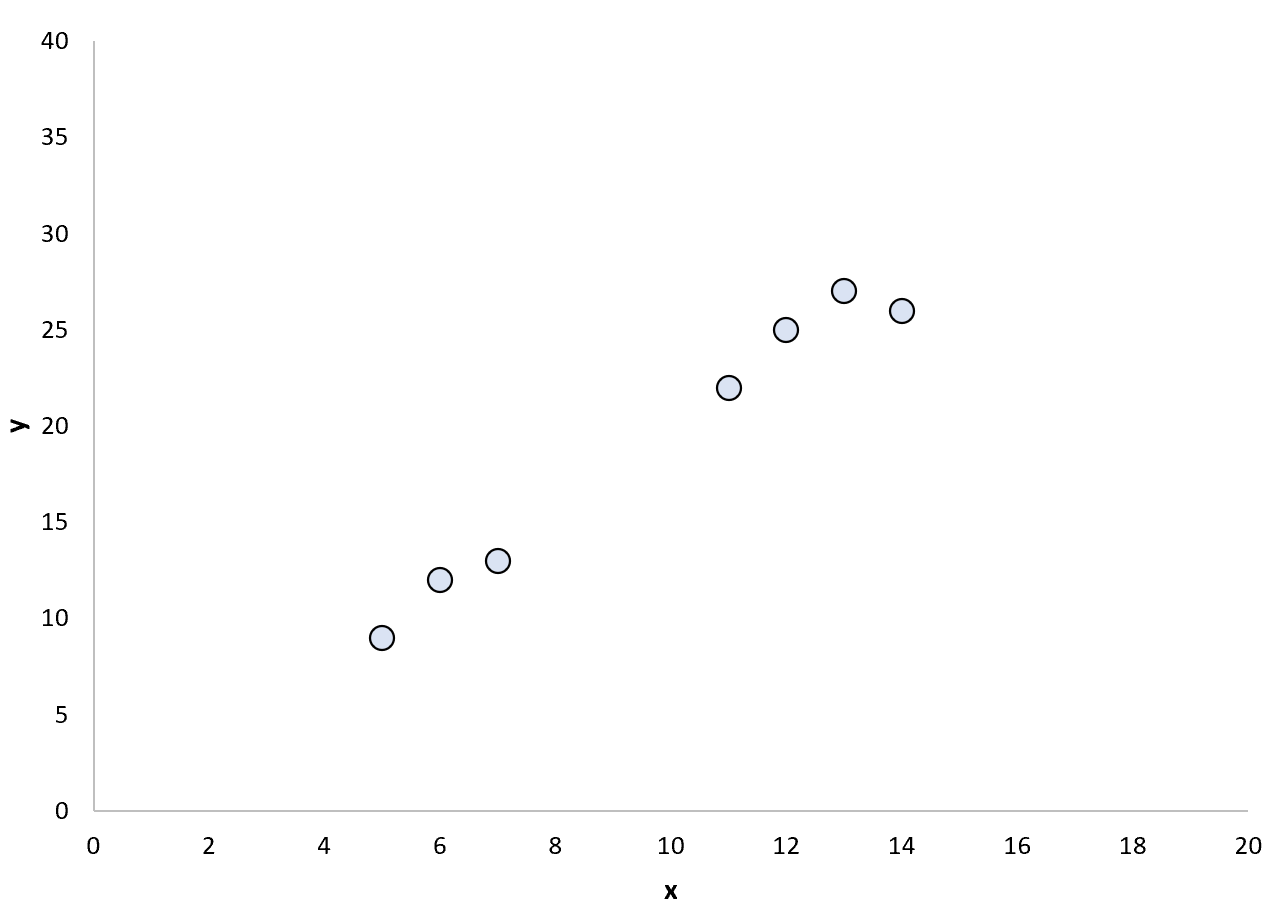
Kita dapat memutuskan untuk menyesuaikan model regresi linier sederhana dengan poin-poin berikut:

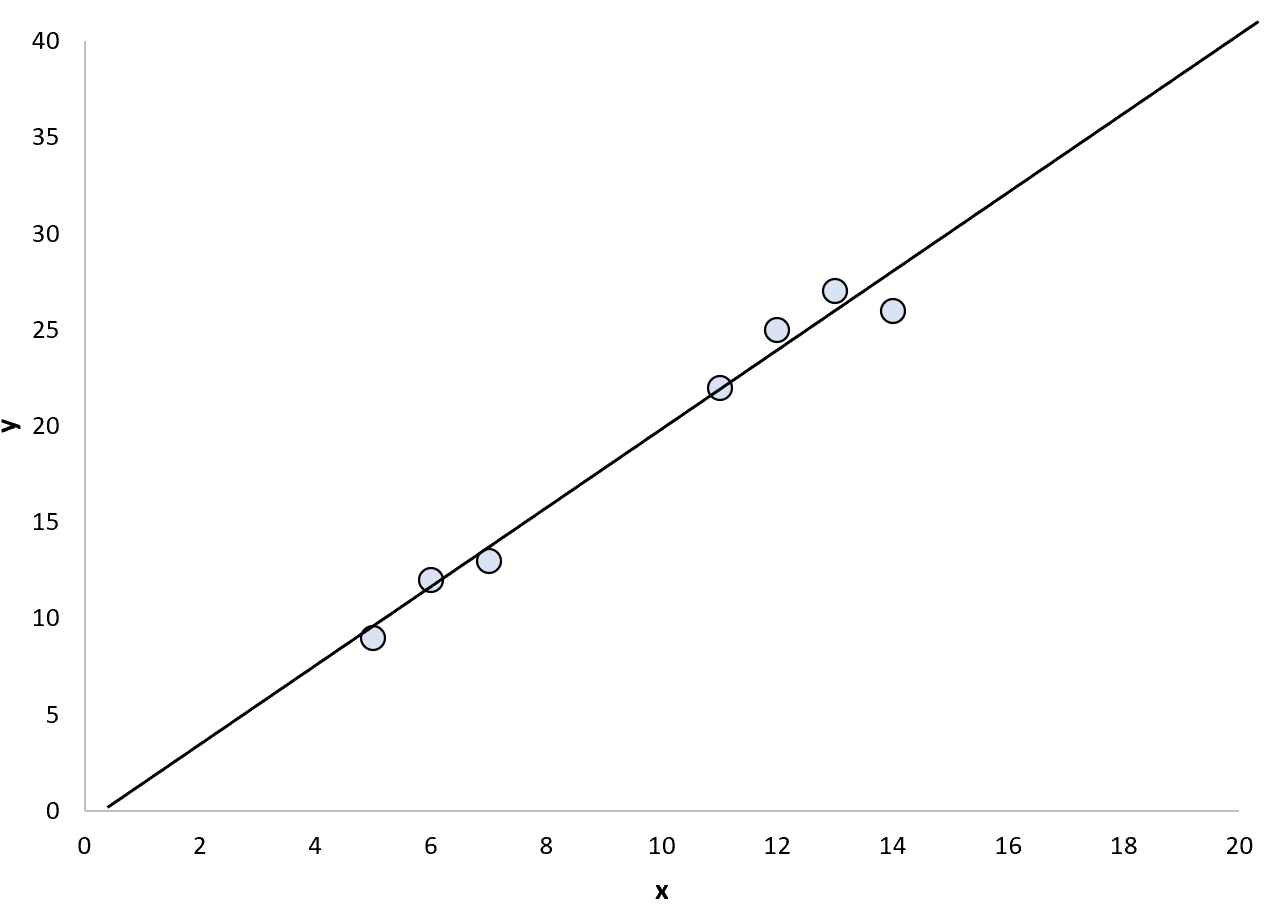
Kami kemudian dapat menggunakan model regresi yang disesuaikan untuk memprediksi nilai titik baik di dalam maupun di luar rentang titik data.

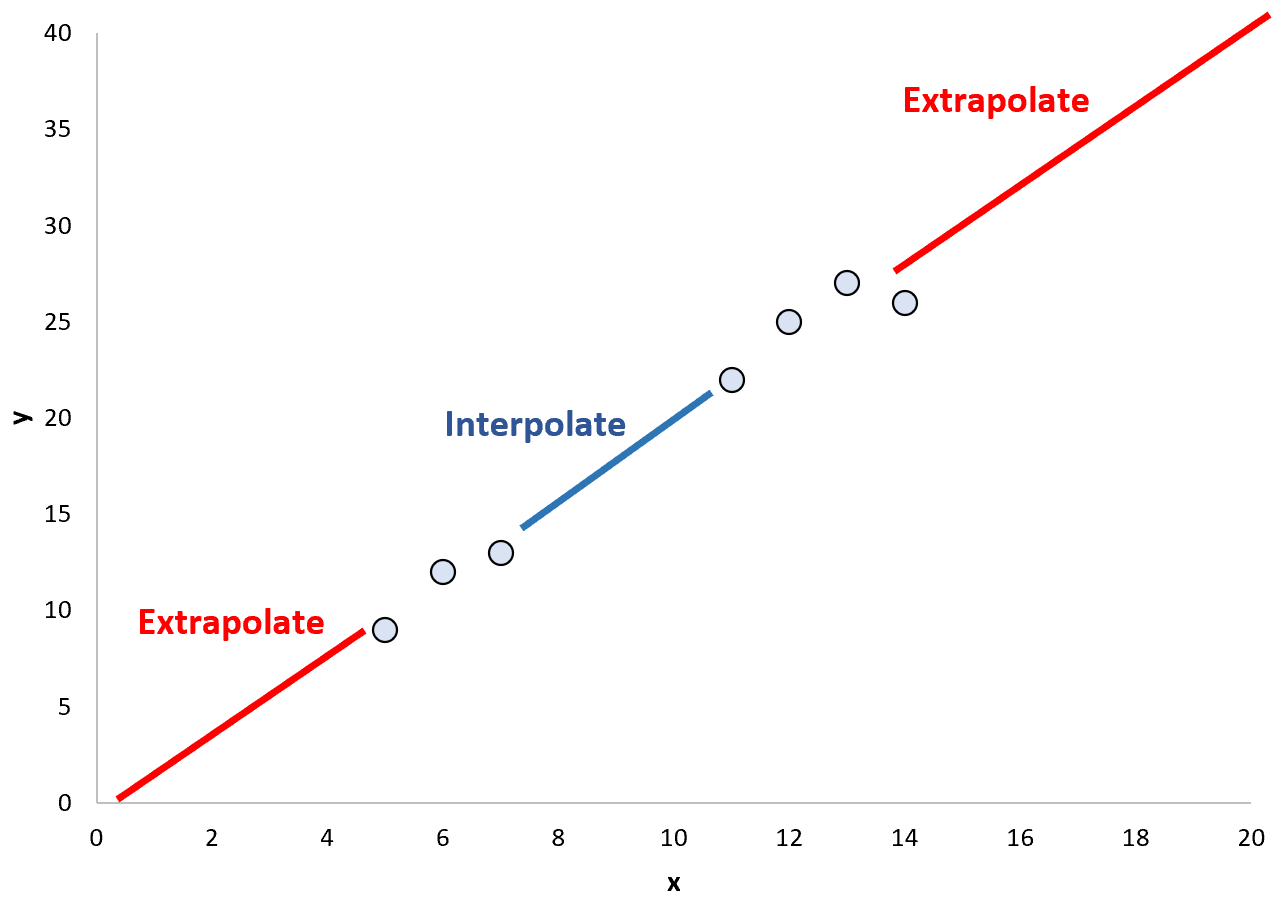
Saat kita menggunakan model regresi yang disesuaikan untuk memprediksi nilai titik dalam rentang titik data yang ada, hal ini disebut interpolasi.

Sebaliknya, bila kita menggunakan model regresi yang disesuaikan untuk memprediksi nilai titik di luar rentang yang ada, hal itu disebut ekstrapolasi :

Potensi bahaya ekstrapolasi

Saat kami melakukan ekstrapolasi, kami berasumsi bahwa pola yang sama yang ada di dalam rentang titik data saat ini juga ada di luar rentang tersebut.

Namun, asumsi ini bisa berbahaya karena ada kemungkinan pola yang ada di luar rentang titik data saat ini sangat berbeda:

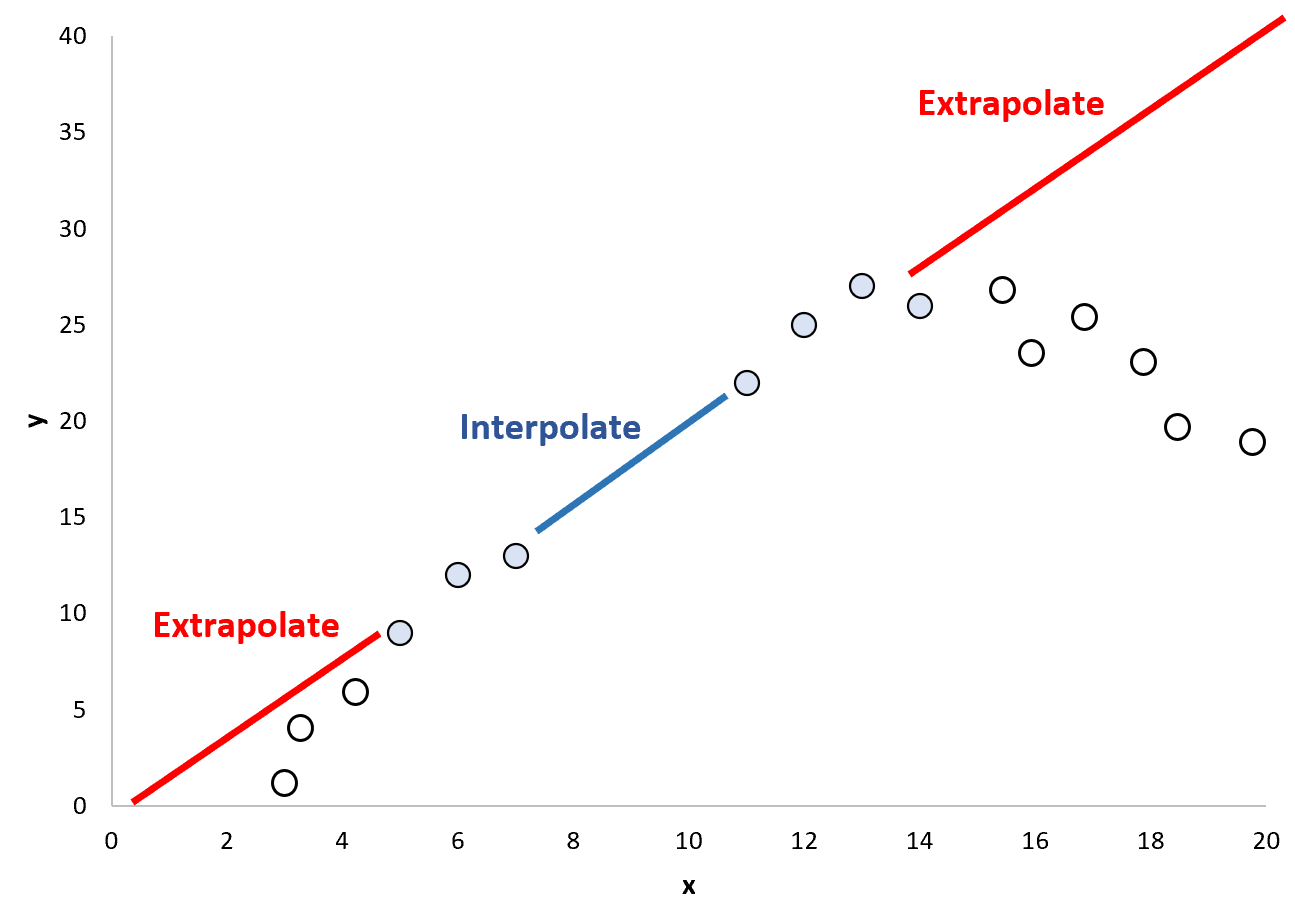
Oleh karena itu, menggunakan ekstrapolasi untuk memprediksi nilai titik data yang berada di luar rentang nilai yang digunakan untuk membuat model regresi bisa berbahaya.

Dalam praktiknya, sering kali masuk akal untuk menggunakan ekstrapolasi untuk memprediksi nilai titik yang berada sedikit di luar rentang nilai yang ada, namun semakin jauh dari rentang tersebut, semakin besar kemungkinan perbedaan antara nilai prediksi dan nilai sebenarnya. nilai itu penting. .

Kapan menggunakan ekstrapolasi

Seringkali diperlukan keahlian khusus domain untuk menentukan apakah ekstrapolasi merupakan ide yang masuk akal atau tidak.

Misalnya, departemen pemasaran suatu perusahaan menerapkan model regresi linier sederhana dengan menggunakan belanja iklan sebagai variabel prediktor dan total pendapatan sebagai variabel respons.

Dalam skenario ini, masuk akal untuk berasumsi bahwa peningkatan belanja iklan yang stabil akan menghasilkan peningkatan total pendapatan yang dapat diprediksi:

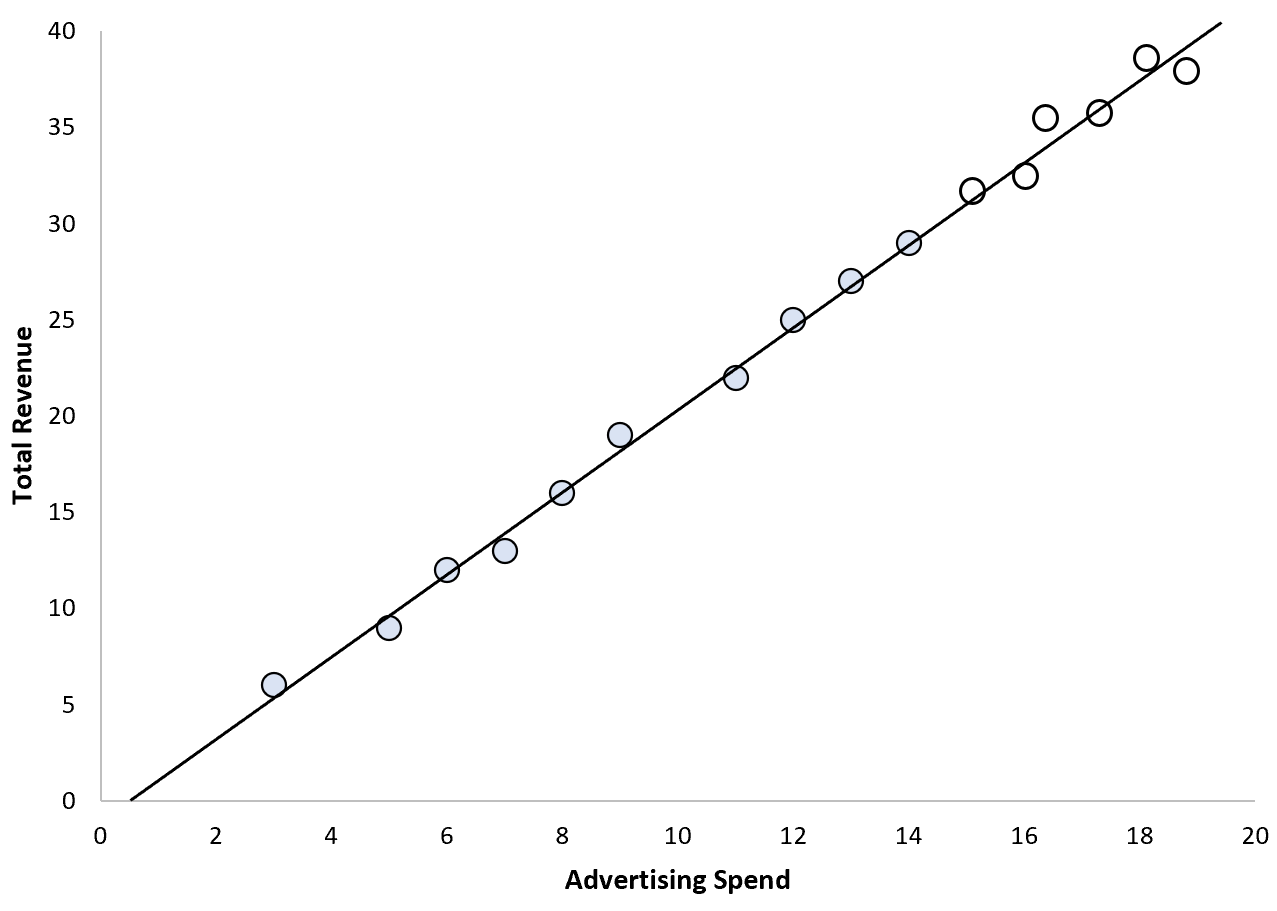
Dalam skenario ini, kita cukup yakin dengan kemampuan kita untuk mengekstrapolasi nilai.

Namun, pertimbangkan skenario di mana seorang ahli biologi ingin menggunakan pupuk total untuk memprediksi pertumbuhan tanaman.

Dia mungkin memutuskan untuk menyesuaikan model regresi linier sederhana dengan titik data, namun karena ada batas atas tinggi tanaman, mungkin tidak masuk akal menggunakan ekstrapolasi untuk memprediksi nilai titik. berada di luar kisaran nilai. nilai yang digunakan agar sesuai dengan model:

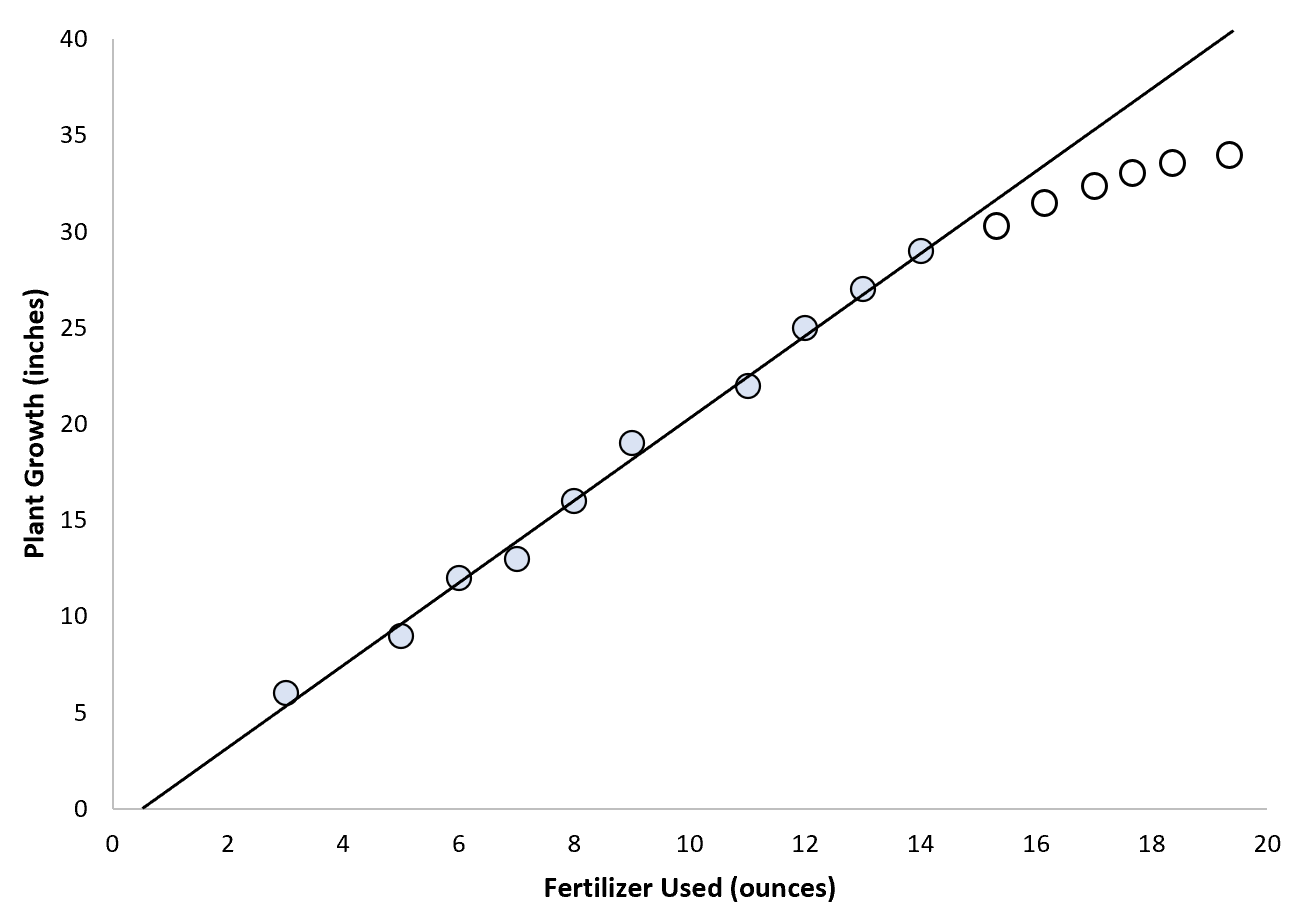
Dalam skenario ini, kita mungkin kurang percaya diri terhadap kemampuan kita memperkirakan nilai.

Kesimpulan : Ekstrapolasi mungkin lebih masuk akal di beberapa area dibandingkan area lainnya, namun selalu ada potensi bahaya bahwa model yang ada dalam rentang nilai yang digunakan untuk menyesuaikan model tidak ada di luar pantai.

Sumber daya tambahan

Cara melakukan interpolasi linier di Excel
Cara membuat prediksi dengan regresi linier