Cara menghitung interval keyakinan poisson (langkah demi langkah)

Distribusi Poisson adalah distribusi probabilitas yang digunakan untuk memodelkan probabilitas sejumlah peristiwa tertentu yang terjadi selama selang waktu tertentu ketika peristiwa-peristiwa tersebut diketahui terjadi secara independen dan dengan laju rata-rata yang konstan.

Meskipun mengetahui jumlah rata-rata kemunculan proses Poisson bermanfaat, akan lebih berguna lagi jika memiliki interval kepercayaan di sekitar jumlah rata-rata kemunculan.

Misalnya, kita mengumpulkan data di pusat panggilan pada hari acak dan melihat jumlah rata-rata panggilan per jam adalah 15.

Karena kami hanya mengumpulkan data untuk satu hari, kami tidak dapat memastikan bahwa pusat panggilan menerima rata-rata 15 panggilan per jam sepanjang tahun.

Namun, kita dapat menggunakan rumus berikut untuk menghitung interval kepercayaan untuk jumlah rata-rata panggilan per jam:

Rumus interval kepercayaan Poisson

Interval kepercayaan = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

Emas:

• X ² : Nilai kritis chi kuadrat
• N : Banyaknya kejadian yang diamati
• α : tingkat signifikansi

Contoh langkah demi langkah berikut mengilustrasikan cara menghitung interval kepercayaan Poisson 95% dalam praktiknya.

Langkah 1: hitung peristiwa yang diamati

Misalkan kita menghitung rata-rata jumlah panggilan per jam di sebuah call center adalah 15. Jadi, N = 15 .

Dan karena kita menghitung interval kepercayaan 95%, kita akan menggunakan α = 0,05 dalam perhitungan berikut.

Langkah 2: Temukan batas bawah interval kepercayaan

Batas bawah selang kepercayaan dihitung sebagai berikut:

• Batas bawah = 0,5*X ² _{2N, α/2}
• Batas bawah = 0,5*X ² _{2(15), 0,975}
• Batas bawah = 0,5*X ² _{30, 0,975}
• Batas bawah = 0,5*16.791
• Batas bawah = 8,40

Catatan: Kami menggunakan kalkulator nilai kritis chi-kuadrat untuk menghitung X ² _{30, 0,975} .

Langkah 3: Temukan batas atas interval kepercayaan

Batas atas selang kepercayaan dihitung sebagai berikut:

• Batas atas = 0,5*X ² _{2(N+1), 1-α/2}
• Batas atas = 0,5*X ² _{2(15+1), 0,025}
• Batas atas = 0,5*X ² _{32, 0,025}
• Batas atas = 0,5*49,48
• Batas atas = 24,74

Catatan: Kami menggunakan kalkulator nilai kritis chi-kuadrat untuk menghitung X ² _32.0.025 .

Langkah 4: Temukan Interval Keyakinan

Dengan menggunakan batas bawah dan atas yang dihitung sebelumnya, interval kepercayaan Poisson 95% kita menjadi:

• CI 95% = [8,40, 24,74]

Artinya, kami yakin 95% bahwa jumlah rata-rata panggilan per jam sebenarnya yang diterima pusat panggilan adalah antara 8,40 panggilan dan 24,74 panggilan.

Bonus: Kalkulator Interval Keyakinan Ikan

Jangan ragu untuk menggunakan kalkulator interval kepercayaan Poisson ini untuk menghitung interval kepercayaan Poisson secara otomatis.

Misalnya, berikut cara menggunakan kalkulator ini untuk mencari interval kepercayaan Poisson yang baru saja kita hitung secara manual:

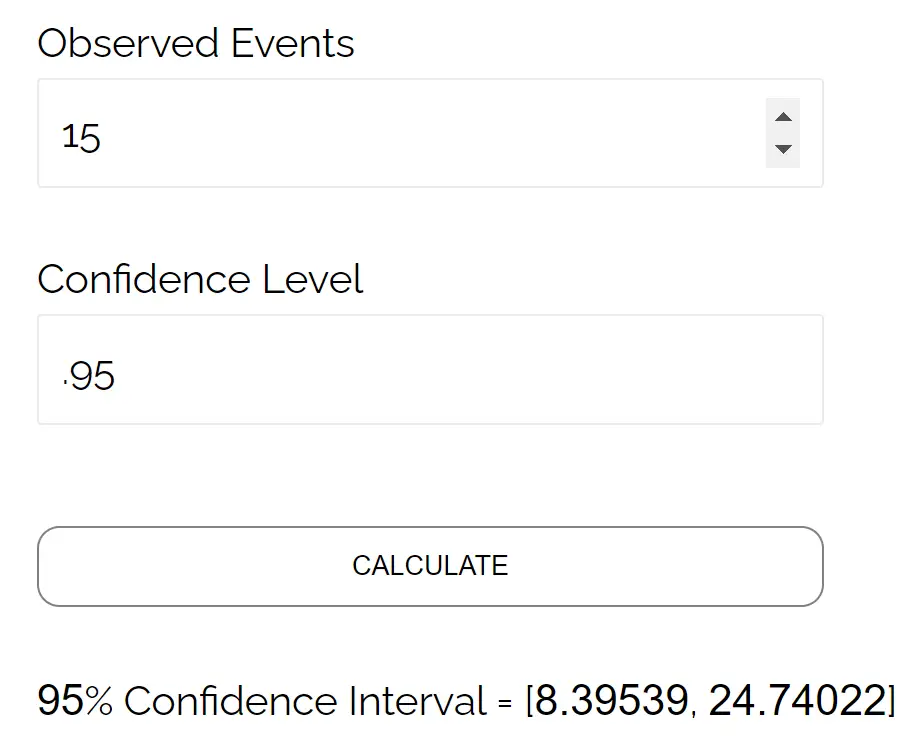
Perhatikan bahwa hasilnya sesuai dengan interval kepercayaan yang kami hitung secara manual.