Cara membuat interval prediksi di excel

Dalam statistik, regresi linier sederhana adalah teknik yang dapat kita gunakan untuk mengukur hubungan antara variabel prediktor, x, dan variabel respon, y.

Saat kita melakukan regresi linier sederhana, kita memperoleh “garis yang paling sesuai” yang menggambarkan hubungan antara x dan y, yang dapat ditulis sebagai:

ŷ = b ₀ + b ₁ x

Emas:

• ŷ adalah nilai prediksi variabel respon
• b ₀ adalah titik potong y
• b ₁ adalah koefisien regresi
• x adalah nilai variabel prediktor

Terkadang kita ingin menggunakan garis yang paling sesuai ini untuk membuat interval prediksi untuk nilai x ₀ tertentu, yang merupakan interval di sekitar nilai prediksi ŷ ₀ sedemikian rupa sehingga terdapat probabilitas 95% bahwa nilai y sebenarnya dalam populasi sesuai dengan x ₀ termasuk dalam interval ini.

Rumus untuk menghitung interval prediksi untuk nilai tertentu x ₀ ditulis:

ŷ ₀ +/- t _α/2,df=n-2 * se

Emas:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

Rumusnya mungkin tampak sedikit menakutkan, namun sebenarnya mudah untuk dihitung di Excel. Selanjutnya kita akan melihat contoh penggunaan rumus ini untuk menghitung interval prediksi untuk nilai tertentu di Excel.

Contoh: Cara Membuat Interval Prediksi di Excel

Dataset berikut menunjukkan jumlah jam belajar serta nilai ujian yang diperoleh 15 siswa berbeda:

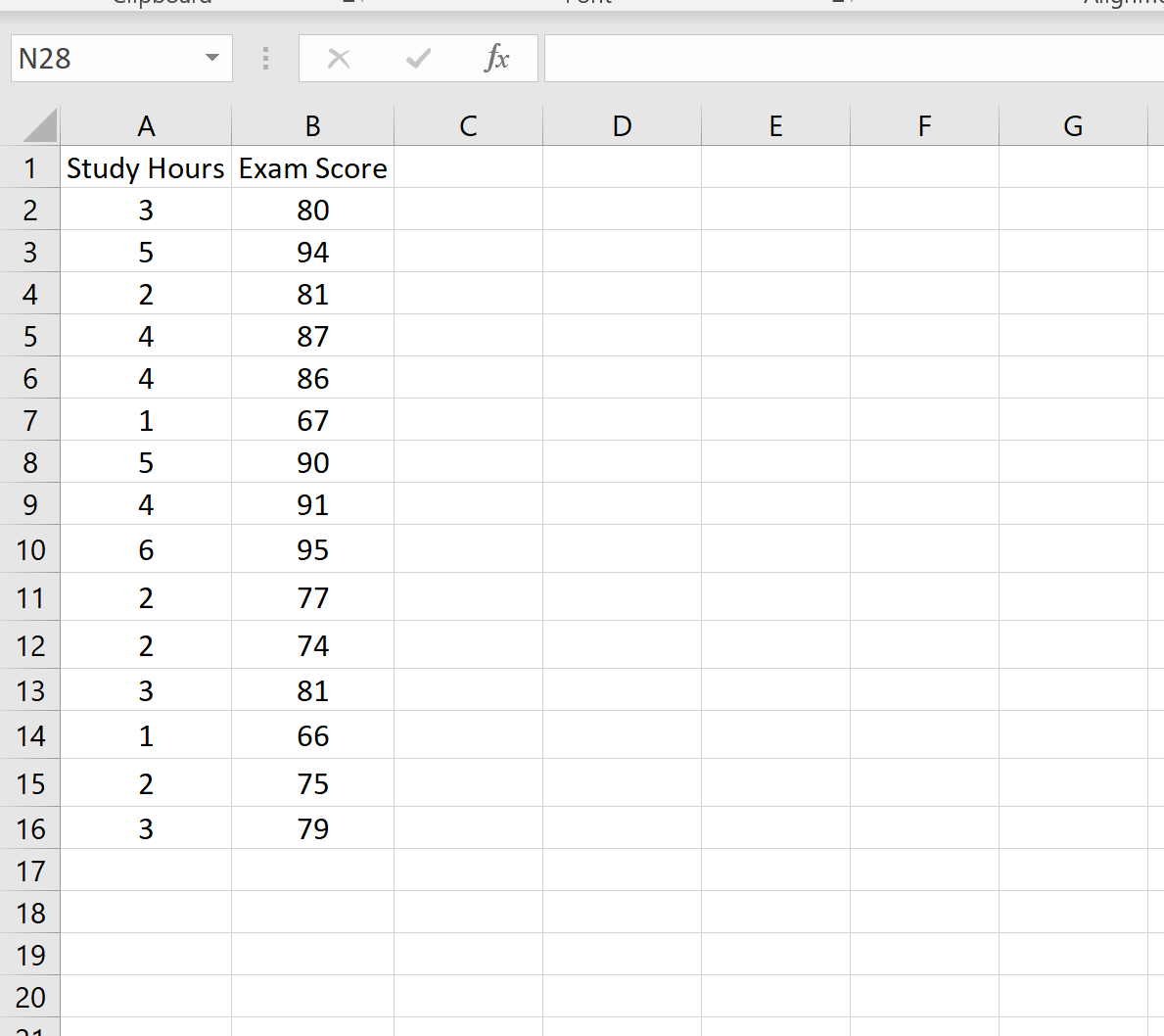
Misalkan kita ingin membuat interval prediksi 95% untuk nilai x ₀ = 3. Artinya, kita ingin membuat interval sedemikian rupa sehingga ada kemungkinan 95% nilai ujian akan berada dalam interval ini untuk siswa yang belajar untuk 3 jam.

Tangkapan layar berikut menunjukkan cara menghitung semua nilai yang diperlukan untuk mendapatkan interval prediksi ini.

Catatan: Rumus di kolom F menunjukkan bagaimana nilai di kolom E dihitung.

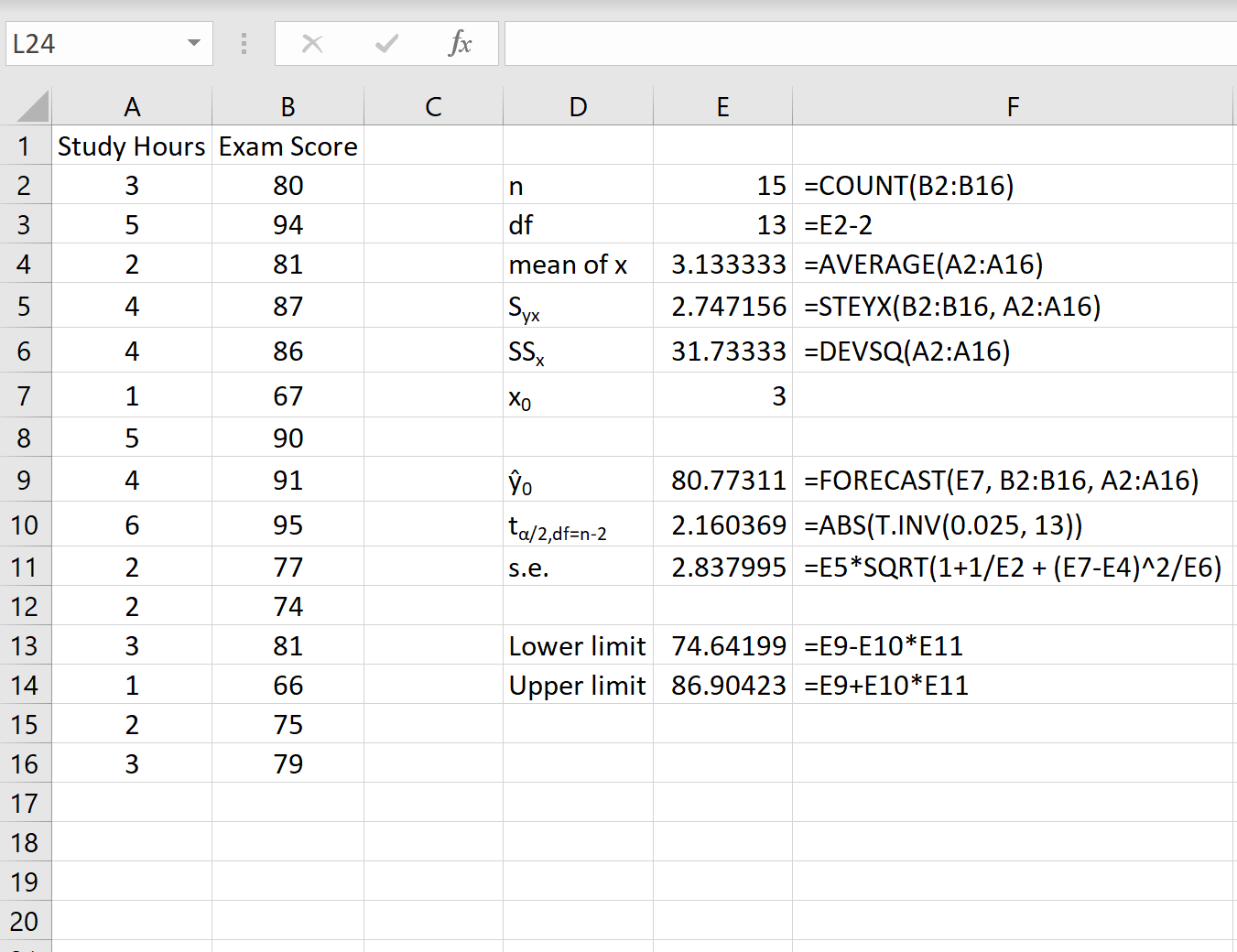
Interval prediksi 95% untuk nilai x ₀ = 3 adalah (74.64, 86.90) . Artinya, kami memperkirakan dengan probabilitas 95% bahwa seorang siswa yang belajar selama 3 jam akan memperoleh nilai antara 74,64 dan 86,90.

Beberapa catatan mengenai perhitungan yang digunakan:

• Untuk menghitung nilai t-kritis dari t _α/2,df=n-2, kita menggunakan α/2 = 0.05/2 = 0.25 karena kita menginginkan interval prediksi sebesar 95%. Perhatikan bahwa interval prediksi yang lebih tinggi (misalnya interval prediksi 99%) akan menghasilkan interval yang lebih lebar. Sebaliknya, interval prediksi yang lebih kecil (misalnya interval prediksi 90%) akan menghasilkan interval yang lebih sempit.
• Kami menggunakan rumus =FORECAST() untuk mendapatkan nilai prediksi ŷ ₀ tetapi rumus =FORECAST.LINEAR() akan mengembalikan nilai yang persis sama.