Cara menafsirkan plot sisa melengkung (dengan contoh)

Plot sisa digunakan untuk menilai apakah sisa model regresi berdistribusi normal dan menunjukkan heteroskedastisitas atau tidak.

Idealnya, Anda ingin titik-titik dalam plot sisa tersebar secara acak di sekitar nilai nol, tanpa pola yang jelas.

Jika Anda menemukan plot sisa yang titik plotnya memiliki pola melengkung, kemungkinan besar model regresi yang Anda tentukan untuk datanya tidak benar.

Dalam kebanyakan kasus, ini berarti Anda telah mencoba menyesuaikan model regresi linier dengan kumpulan data yang mengikuti tren kuadrat.

Contoh berikut menunjukkan cara menafsirkan (dan memperbaiki) plot sisa melengkung dalam praktiknya.

Contoh: Menafsirkan plot sisa yang melengkung

Misalkan kita mengumpulkan data berikut mengenai jumlah jam kerja per minggu dan tingkat kebahagiaan yang dilaporkan (dalam skala 0 hingga 100) untuk 11 orang berbeda di sebuah kantor:

Jika kita membuat diagram sebar sederhana antara jam kerja versus tingkat kebahagiaan, tampilannya akan seperti ini:

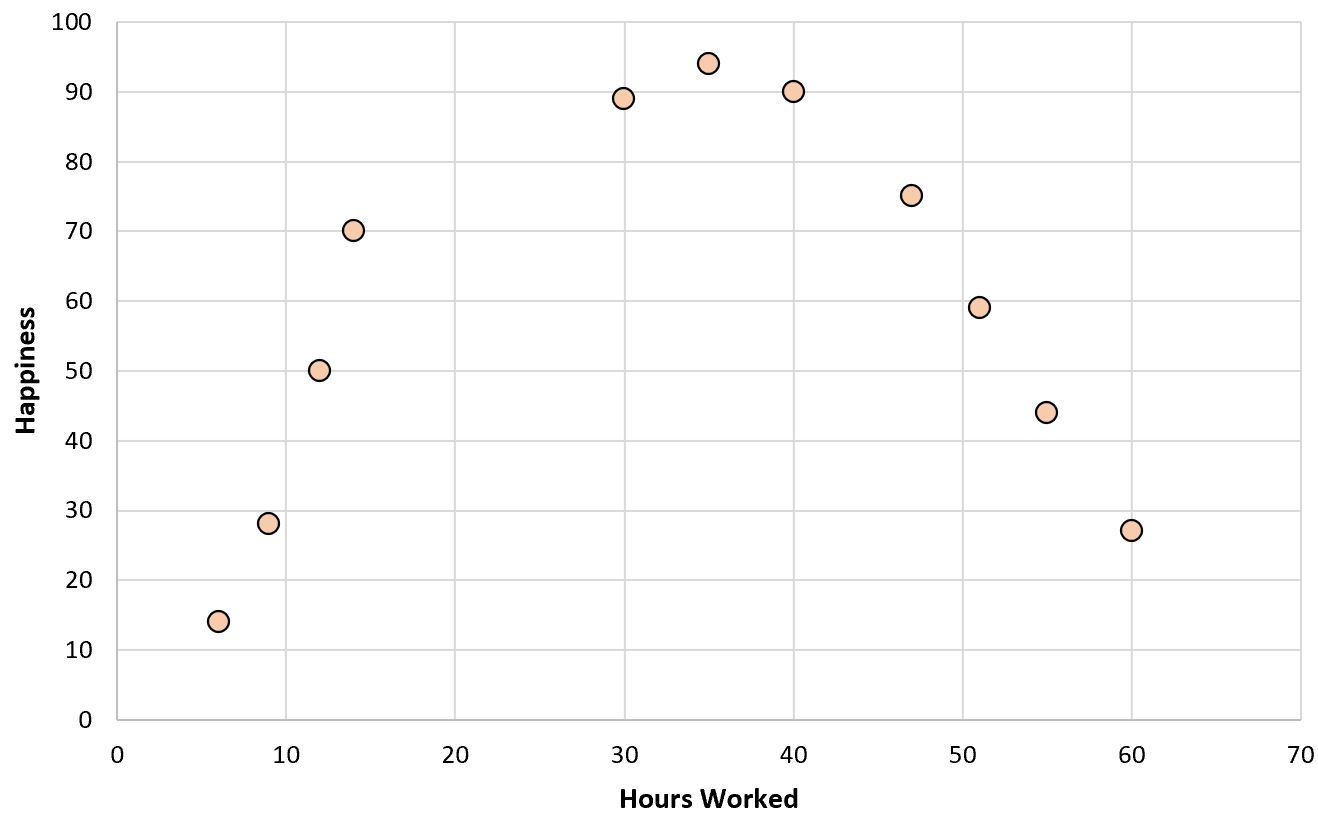
Sekarang anggaplah kita ingin menyesuaikan model regresi menggunakan jam kerja untuk memprediksi tingkat kebahagiaan.

Kode berikut menunjukkan cara menyesuaikan model regresi linier sederhana ke kumpulan data ini dan menghasilkan plot sisa di R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#fit linear regression model
linear_model <- lm(happiness ~ hours, data=df)

#get list of residuals 
res <- resid(linear_model)

#produce residual vs. fitted plot
plot(fitted(linear_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0)

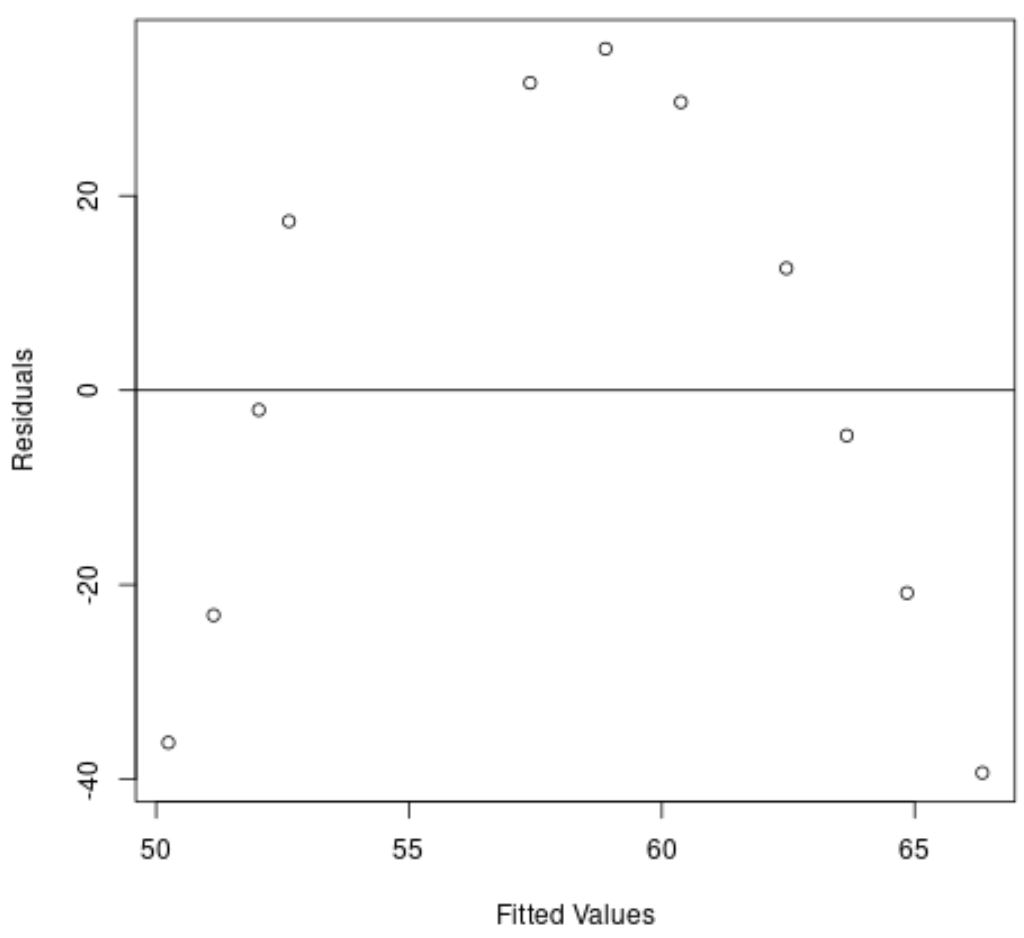
Sumbu x menampilkan nilai yang dipasang dan sumbu y menampilkan residu.

Dari grafik tersebut terlihat adanya pola melengkung pada residu yang menunjukkan bahwa model regresi linier tidak memberikan kecocokan yang sesuai dengan kumpulan data tersebut.

Kode berikut menunjukkan cara menyesuaikan model regresi kuadratik dengan kumpulan data ini dan menghasilkan plot sisa di R:

 #create dataframe
df <- data. frame (hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                 happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))
#define quadratic term to use in model
df$hours2 <- df$hours^2

#fit quadratic regression model
quadratic_model <- lm(happiness ~ hours + hours2, data=df)

#get list of residuals 
res <- resid(quadratic_model)

#produce residual vs. fitted plot
plot(fitted(quadratic_model), res, xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

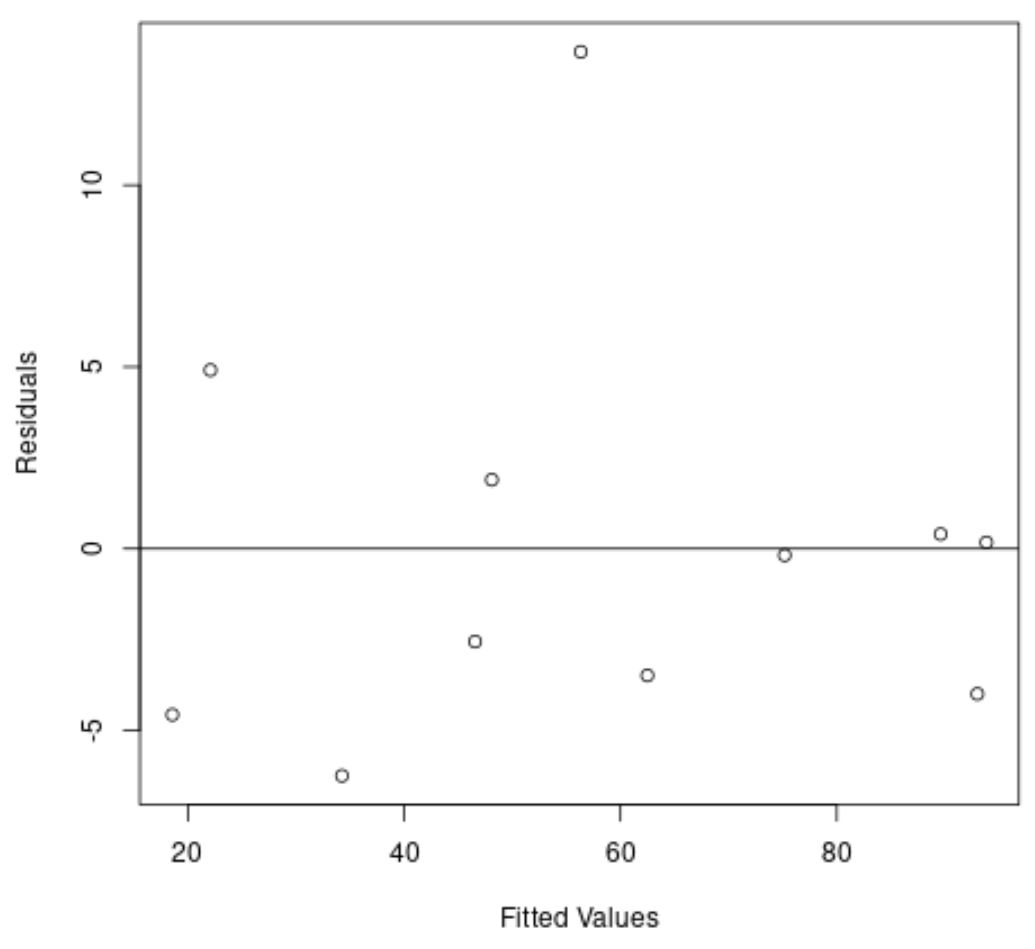
Sekali lagi, sumbu x menunjukkan nilai yang dipasang dan sumbu y menunjukkan residu.

Dari plot tersebut terlihat bahwa residu tersebar secara acak di sekitar nol dan tidak ada tren yang jelas pada residu tersebut.

Hal ini menunjukkan bahwa model regresi kuadratik melakukan tugasnya jauh lebih baik dalam menyesuaikan kumpulan data dibandingkan model regresi linier.

Hal ini masuk akal mengingat kita melihat bahwa hubungan sebenarnya antara jam kerja dan tingkat kebahagiaan tampak bersifat kuadratik dan bukan linier.

Sumber daya tambahan

Tutorial berikut menjelaskan cara membuat plot sisa menggunakan perangkat lunak statistik yang berbeda:

Cara Membuat Jalur Sisa dengan Tangan
Cara membuat plot sisa di R
Cara Membuat Plot Sisa di Excel
Cara Membuat Plot Sisa dengan Python