Jenis asimetri

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Pada artikel ini Anda akan mempelajari berapa banyak jenis asimetri yang ada dalam statistik. Dengan demikian, setiap jenis asimetri dijelaskan dengan contoh dan, sebagai tambahan, Anda akan dapat melihat bagaimana asimetri suatu distribusi dihitung.

Apa saja jenis-jenis asimetri?

Dalam statistik, ada tiga jenis asimetri :

Kecondongan positif : Distribusi mempunyai nilai yang lebih berbeda di sebelah kanan mean daripada di sebelah kiri.
Kecondongan negatif : Distribusi mempunyai nilai yang lebih berbeda di sebelah kiri mean daripada di sebelah kanannya.
Simetri : Distribusi mempunyai jumlah nilai yang sama di kiri dan kanan mean.

Setiap jenis asimetri dijelaskan lebih detail di bawah.

asimetri positif

Jika suatu distribusi mempunyai kemiringan positif , berarti grafiknya memiliki ekor kanan yang lebih panjang daripada ekor kiri. Artinya, distribusi mempunyai nilai yang lebih berbeda di sebelah kanan mean.

Kurva pada contoh sebelumnya bersifat asimetris positif karena terdapat lebih banyak nilai di sebelah kanan mean daripada di sebelah kiri. Seperti yang dapat Anda lihat dari grafik, bilah yang ditunjukkan dalam warna hijau jauh lebih besar dibandingkan bilah oranye.

asimetri negatif

Dalam statistik, suatu distribusi dikatakan memiliki kemiringan negatif jika grafiknya memiliki ekor kiri yang lebih panjang daripada ekor kanannya. Artinya, distribusi yang condong negatif berarti mempunyai nilai yang lebih berbeda di sebelah kiri mean.

Jika melihat grafik sebelumnya, terdapat lebih banyak nilai di sebelah kiri mean daripada di sebelah kanan, sehingga kurvanya miring ke negatif.

Simetri

Suatu distribusi dikatakan simetris jika banyaknya nilai di sebelah kiri mean sama dengan banyaknya nilai di sebelah kanan mean. Oleh karena itu, rata-rata bertindak sebagai sumbu simetri.

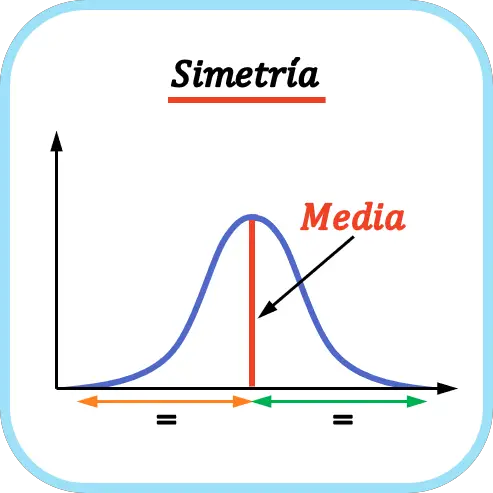
Seperti terlihat pada contoh di atas, banyaknya nilai di sebelah kiri mean dari distribusi probabilitas yang diwakili bertepatan dengan banyaknya nilai di sebelah kanan mean, sehingga merupakan distribusi simetris.

Cara menentukan jenis asimetri

Sekarang setelah kita mengetahui berbagai jenis asimetri dalam statistik, mari kita lihat cara mengetahui jenis asimetri yang sesuai dengan distribusi probabilitas.

Secara tradisional dijelaskan bahwa kita dapat mengetahui jenis skewness suatu distribusi berdasarkan hubungan antara mean dan mediannya (apakah lebih besar, setara, atau lebih kecil). Namun, properti ini tidak selalu memuaskan. Jadi, untuk menentukan skewness suatu distribusi, koefisien skewness Fisher harus dihitung.

Koefisien asimetri Fisher dihitung menggunakan rumus berikut:

$\displaystyle\gamma_1=E\left[\left(\frac{X-\mu}{\sigma}\right)^3 \right]$

Atau setara:

$\displaystyle\gamma_1=\frac{\operatorname{E}[X^3] - 3\mu\sigma^2 - \mu^3}{\sigma^3}$

Emas

$E$

adalah ekspektasi matematis ,

$\mu$

mean aritmatika dan

$\sigma$

deviasi standar .

Dan setelah koefisien Fisher dihitung, tandanya memungkinkan untuk menentukan jenis asimetri distribusi yang muncul:

Jika koefisien skewness Fisher bernilai positif, maka distribusinya pun skew positif.
Jika koefisien skewness Fisher bernilai negatif, maka distribusinya juga skewness negatif.
Jika distribusinya simetris, koefisien skewness Fisher sama dengan nol (kebalikannya tidak selalu benar).

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya