Jenis rata-rata (statistik)

Oleh Benjamin anderson Agustus 6, 2023 Statistik 0 Komentar

Di sini kami menjelaskan apa saja jenis rata-rata dalam statistik dan cara menghitungnya. Anda akan menemukan rumus untuk setiap jenis stocking dan contohnya.

Namun sebelum melihat apa saja jenis-jenis rata-rata, kita harus mengetahui secara logika apa itu rata-rata dalam statistik. Oleh karena itu, kami menyarankan Anda membaca tautan berikut sebelum melanjutkan.

➤ Lihat: Berapa rata-ratanya (statistik)?

Apa saja jenis rata-rata dalam statistik?

Dalam statistik, jenis rata-rata adalah:

Rata-rata aritmatika
Rata-rata tertimbang
Artinya geometris
akar berarti persegi
makna harmonis
rata-rata umum
f-rata-rata yang digeneralisasi
berarti dipangkas
rata-rata antarkuartil
rata-rata suatu fungsi

Selanjutnya kami akan menjelaskan cara menghitung semua jenis rata-rata dalam statistik. Lima jenis rata-rata yang paling umum digunakan adalah rata-rata aritmatika, rata-rata tertimbang, rata-rata geometri, rata-rata kuadrat, dan rata-rata harmonik. Jadi kita akan membahas lebih detail tentang lima jenis media utama ini.

Rata-rata aritmatika

Rata-rata aritmatika dihitung dengan menjumlahkan semua nilai dan kemudian membaginya dengan jumlah total titik data.

Oleh karena itu, rumus rata-rata aritmatika adalah sebagai berikut:

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

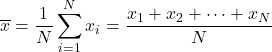
Rata-rata aritmatika juga dikenal sebagai mean aritmatika .

Rata-rata aritmatika mungkin merupakan jenis rata-rata yang paling banyak digunakan dalam statistik.

Untuk melihat contoh cara memperoleh rata-rata jenis ini, kita akan menghitung rata-rata aritmatika dari data berikut:

$4\quad 7\quad 10\quad 1\quad 8\quad9$

Untuk menghitung mean aritmatika, cukup jumlahkan semua data statistik dan bagi dengan jumlah data, yaitu 6:

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

Rata-rata tertimbang

Untuk menghitung rata-rata tertimbang, pertama-tama Anda harus mengalikan setiap data statistik dengan bobotnya (atau bobotnya), lalu menjumlahkan semua hasil kali, dan terakhir membagi jumlah tertimbang dengan jumlah semua bobot.

Oleh karena itu, rumus rata-rata tertimbangnya adalah sebagai berikut:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

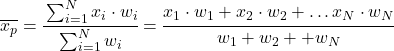
Dimana x _i adalah nilai statistik dan w _i bobotnya.

Rata-rata tertimbang lebih sulit dipahami, jadi sebaiknya lihat contoh berikut yang menjelaskan langkah demi langkah cara menghitungnya:

➤ Lihat: Contoh rata-rata tertimbang

Artinya geometris

Rata-rata geometrik sekumpulan data statistik sama dengan akar ke-n hasil perkalian semua nilai.

Jenis rata-rata ini digunakan dalam keuangan bisnis untuk menghitung tingkat pengembalian, rata-rata persentase, dan bunga majemuk.

Rumus penyimpanan jenis ini cukup rumit. Faktanya, rata-rata geometrik dari semua kumpulan statistik tidak dapat dihitung, tetapi terkadang jenis rata-rata ini tidak dapat ditentukan. Inilah sebabnya kami menyarankan Anda melihat semua pengecualian yang dijelaskan di tautan berikut:

➤ Lihat: rumus rata-rata geometri

akar berarti persegi

Root mean square sama dengan akar kuadrat dari mean aritmatika kuadrat data.

Oleh karena itu, rumus kuadrat rata-ratanya adalah sebagai berikut:

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

Jenis rata-rata ini disebut juga root mean square , root mean square, atau RMS .

Mari kita tunjukkan bahwa rata-rata kubik juga ada, tetapi digunakan dalam kasus-kasus yang sangat khusus.

Rata-rata kuadrat memiliki kelebihan dan kekurangan, misalnya sangat berguna ketika variabel statistik bernilai positif dan negatif, karena dengan mengkuadratkan setiap bagian data, semua nilai menjadi positif. Anda dapat melihat lebih banyak fitur dari jenis media ini dengan mengklik link berikut:

➤ Lihat: kelebihan dan kekurangan root mean square

makna harmonis

Rata-rata harmonik dihitung dengan membagi jumlah total data statistik dengan jumlah kebalikan dari setiap nilai.

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

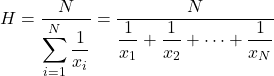
Rata-rata harmonik digunakan untuk menghitung kecepatan rata-rata, waktu atau membuat perhitungan elektronik. Karakteristik ini membedakan rata-rata harmonik dari jenis rata-rata lainnya, yang sering digunakan dalam penghitungan rata-rata harga atau persentase.

Contoh penghitungan rata-rata jenis ini dapat Anda lihat pada halaman berikut:

➤ Lihat: contoh makna harmonis

Jenis stoking lainnya

Pada bagian ini kita akan melihat rumus untuk jenis stocking lainnya. Kami tidak akan menjelaskan secara detail masing-masing jenisnya karena penggunaannya tidak banyak, namun ada baiknya Anda mengetahui bahwa ada jenis stocking lainnya.

Rata-rata umum adalah campuran dari jenis rata-rata yang terlihat di atas dan dihitung menggunakan rumus berikut:

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

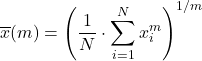
Misalkan f merupakan fungsi injektif dan monotonik, maka f-mean umum didefinisikan sebagai:

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

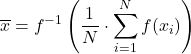
Rata-rata terpangkas melibatkan penghitungan rata-rata aritmatika setelah mengurangkan persentase pengamatan pada ujung atas dan bawah sampel. Persentase yang sama harus ditolak di kedua ujungnya.

Untuk menghitung rata-rata antarkuartil , disebut juga rata-rata antarkuartil, data dari kuartil pertama dan keempat dibuang terlebih dahulu, lalu rata-rata aritmatika kuartil kedua dan ketiga dari sampel saja dihitung. Oleh karena itu, rumus untuk rata-rata jenis ini adalah:

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

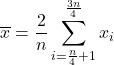
Terakhir, Anda juga dapat menemukan mean suatu fungsi . Nilai rata-rata suatu fungsi kontinu pada interval tertutup [a,b] dihitung dengan menggunakan rumus berikut:

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

Rata-rata sampel dan populasi

Terakhir, kita akan melihat perbedaan antara rata-rata sampel dan rata-rata populasi, dua jenis rata-rata yang sering membingungkan.

Rata-rata sampel adalah rata-rata yang dihitung atas nilai-nilai sampel statistik, artinya dihitung atas sebagian dari semua nilai suatu variabel.

Rata-rata populasi adalah rata-rata yang dihitung atas suatu populasi statistik, yaitu seluruh nilai suatu variabel. Oleh karena itu, mean populasi bertepatan dengan ekspektasi matematis dari variabel tersebut.

Rata-rata sampel dapat dianggap hampir sama dengan rata-rata populasi jika diketahui sejumlah data yang cukup besar. Namun nilai mean populasi sangat sulit diperoleh, karena pada kenyataannya semua nilai suatu distribusi jarang diketahui.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya