Pengelompokan k-means di r: contoh langkah-demi-langkah

Clustering adalah teknik pembelajaran mesin yang mencoba menemukan kelompok observasi dalam kumpulan data.

Tujuannya adalah untuk menemukan klaster sedemikian rupa sehingga pengamatan dalam setiap klaster cukup mirip satu sama lain, sedangkan observasi dalam klaster yang berbeda sangat berbeda satu sama lain.

Pengelompokan adalah bentuk pembelajaran tanpa pengawasan karena kita hanya mencoba menemukan struktur dalam kumpulan data daripada memprediksi nilai variabel respons .

Clustering sering digunakan dalam pemasaran ketika bisnis memiliki akses ke informasi seperti:

• Pendapatan rumah tangga
• Ukuran rumah tangga
• Profesi Kepala Rumah Tangga
• Jarak ke daerah perkotaan terdekat

Ketika informasi ini tersedia, pengelompokan dapat digunakan untuk mengidentifikasi rumah tangga yang serupa dan mungkin lebih cenderung membeli produk tertentu atau memberikan respons yang lebih baik terhadap jenis iklan tertentu.

Salah satu bentuk pengelompokan yang paling umum dikenal sebagai pengelompokan k-means .

Apa itu Pengelompokan K-Means?

K-means clustering adalah teknik di mana kita menempatkan setiap observasi dari suatu dataset ke dalam salah satu K cluster.

Tujuan akhirnya adalah untuk memiliki K cluster dimana pengamatan dalam setiap cluster cukup mirip satu sama lain, sedangkan observasi dalam cluster yang berbeda sangat berbeda satu sama lain.

Dalam praktiknya, kami menggunakan langkah-langkah berikut untuk melakukan pengelompokan K-means:

1. Pilih nilai untuk K.

• Pertama, kita perlu memutuskan berapa banyak cluster yang ingin kita identifikasi dalam data. Seringkali kita hanya perlu menguji beberapa nilai K yang berbeda dan menganalisis hasilnya untuk melihat jumlah cluster mana yang paling masuk akal untuk masalah tertentu.

2. Secara acak tetapkan setiap observasi ke cluster awal, dari 1 sampai K.

3. Lakukan prosedur berikut hingga penetapan cluster berhenti berubah.

• Untuk setiap cluster K , hitung pusat gravitasi cluster tersebut. Ini hanyalah vektor fitur p- mean untuk observasi cluster ke-k .
• Tetapkan setiap observasi ke cluster dengan centroid terdekat. Di sini, jarak terdekat ditentukan menggunakan jarak Euclidean .

Pengelompokan K-Means di R

Tutorial berikut memberikan contoh langkah demi langkah tentang cara melakukan k-means clustering di R.

Langkah 1: Muat paket yang diperlukan

Pertama, kita akan memuat dua paket yang berisi beberapa fungsi berguna untuk pengelompokan k-means di R.

 library (factoextra)
library (cluster)

Langkah 2: Muat dan Siapkan Data

Untuk contoh ini, kita akan menggunakan kumpulan data USArrests yang dibangun ke dalam R, yang berisi jumlah penangkapan per 100.000 orang di setiap negara bagian AS pada tahun 1973 karena pembunuhan , penyerangan , dan pemerkosaan , serta persentase populasi setiap negara bagian yang tinggal di daerah perkotaan. daerah. , UrbanPop .

Kode berikut menunjukkan cara melakukan hal berikut:

• Muat kumpulan data Penangkapan AS
• Hapus semua baris dengan nilai yang hilang
• Skalakan setiap variabel dalam kumpulan data agar memiliki rata-rata 0 dan deviasi standar 1

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Langkah 3: Temukan jumlah cluster yang optimal

Untuk melakukan pengelompokan k-means di R, kita dapat menggunakan fungsi kmeans() bawaan, yang menggunakan sintaks berikut:

kmeans (data, pusat, nstart)

Emas:

• data : Nama kumpulan data.
• pusat: Jumlah cluster, dilambangkan k .
• nstart: jumlah konfigurasi awal. Karena mungkin saja cluster awal yang berbeda akan memberikan hasil yang berbeda, disarankan untuk menggunakan beberapa konfigurasi awal yang berbeda. Algoritma k-means akan mencari konfigurasi awal yang menghasilkan variasi terkecil dalam cluster.

Karena kita tidak mengetahui sebelumnya berapa banyak cluster yang optimal, kita akan membuat dua grafik berbeda yang dapat membantu kita memutuskan:

1. Jumlah cluster relatif terhadap total jumlah kuadrat

Pertama, kita akan menggunakan fungsi fviz_nbclust() untuk membuat plot jumlah cluster versus total jumlah kuadrat:

 fviz_nbclust(df, kmeans, method = “ wss ”) 

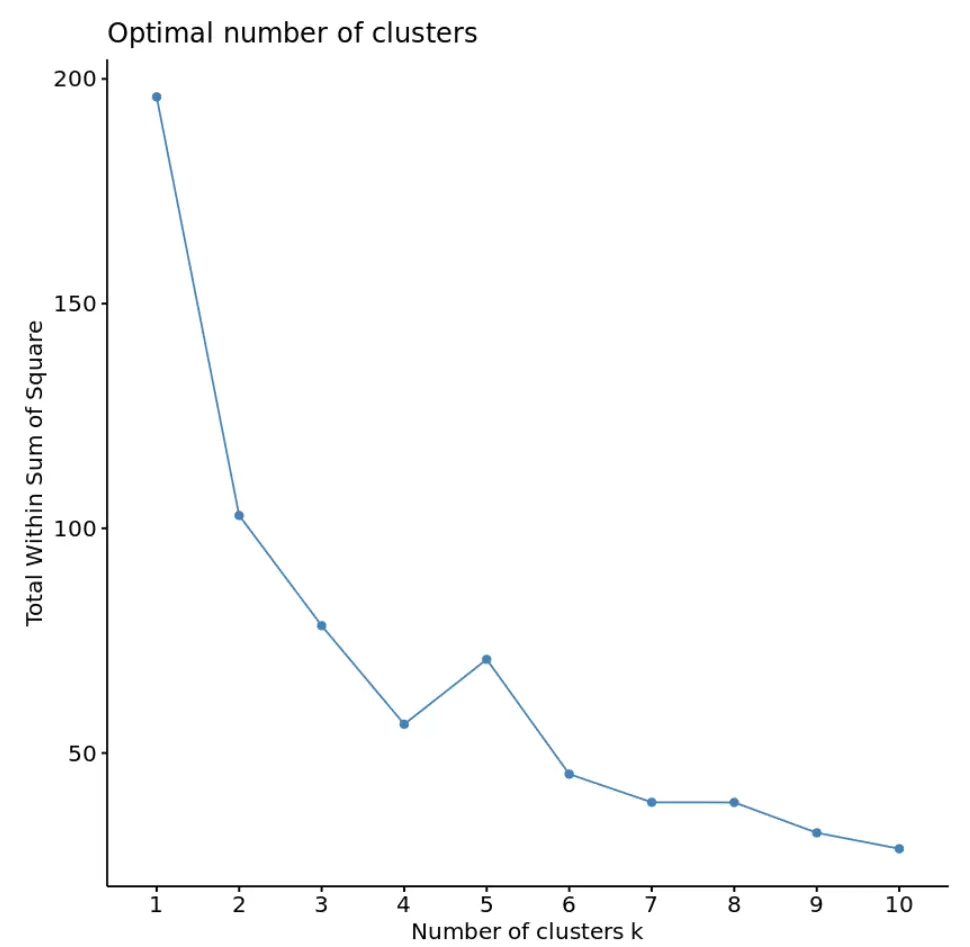
Biasanya, saat kita membuat plot jenis ini, kita mencari “lutut” di mana jumlah kotak mulai “membungkuk” atau mendatar. Biasanya ini adalah jumlah cluster yang optimal.

Untuk grafik ini terlihat terdapat kekusutan atau “tikungan” kecil pada k = 4 cluster.

2. Statistik jumlah klaster versus kesenjangan

Cara lain untuk menentukan jumlah cluster yang optimal adalah dengan menggunakan metrik yang disebut statistik deviasi , yang membandingkan total variasi intra-cluster untuk nilai k yang berbeda dengan nilai yang diharapkan untuk distribusi tanpa pengelompokan.

Kita dapat menghitung statistik kesenjangan untuk setiap jumlah cluster menggunakan fungsi clusGap() dari paket cluster serta memplot cluster terhadap statistik kesenjangan menggunakan fungsi fviz_gap_stat() :

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = kmeans,
                    nstart = 25,
                    K.max = 10,
                    B = 50)

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

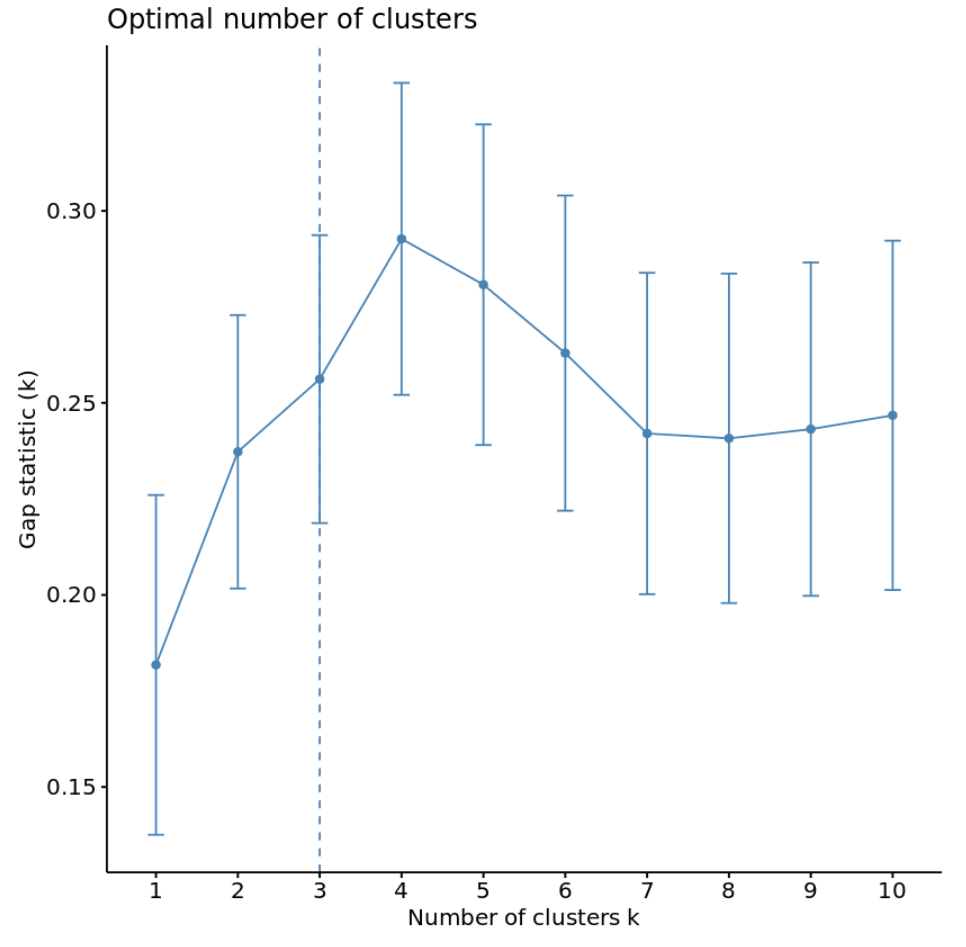
Dari grafik terlihat bahwa statistik gap paling tinggi pada k = 4 cluster, yang sesuai dengan metode siku yang kita gunakan sebelumnya.

Langkah 4: Lakukan K-Means Clustering dengan K Optimal

Terakhir, kita dapat melakukan k-means clustering pada dataset menggunakan nilai optimal k sebesar 4:

 #make this example reproducible
set.seed(1)

#perform k-means clustering with k = 4 clusters
km <- kmeans(df, centers = 4, nstart = 25)

#view results
km

K-means clustering with 4 clusters of sizes 16, 13, 13, 8

Cluster means:
      Murder Assault UrbanPop Rape
1 -0.4894375 -0.3826001 0.5758298 -0.26165379
2 -0.9615407 -1.1066010 -0.9301069 -0.96676331
3 0.6950701 1.0394414 0.7226370 1.27693964
4 1.4118898 0.8743346 -0.8145211 0.01927104

Vector clustering:
       Alabama Alaska Arizona Arkansas California Colorado 
             4 3 3 4 3 3 
   Connecticut Delaware Florida Georgia Hawaii Idaho 
             1 1 3 4 1 2 
      Illinois Indiana Iowa Kansas Kentucky Louisiana 
             3 1 2 1 2 4 
         Maine Maryland Massachusetts Michigan Minnesota Mississippi 
             2 3 1 3 2 4 
      Missouri Montana Nebraska Nevada New Hampshire New Jersey 
             3 2 2 3 2 1 
    New Mexico New York North Carolina North Dakota Ohio Oklahoma 
             3 3 4 2 1 1 
        Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee 
             1 1 1 4 2 4 
         Texas Utah Vermont Virginia Washington West Virginia 
             3 1 2 1 1 2 
     Wisconsin Wyoming 
             2 1 

Within cluster sum of squares by cluster:
[1] 16.212213 11.952463 19.922437 8.316061
 (between_SS / total_SS = 71.2%)

Available components:

[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"   
[7] "size" "iter" "ifault"         

Dari hasilnya kita dapat melihat bahwa:

• 16 negara bagian ditugaskan ke cluster pertama
• 13 negara bagian telah ditugaskan ke cluster kedua
• 13 negara bagian telah ditugaskan ke cluster ketiga
• 8 negara bagian telah ditugaskan ke cluster keempat

Kita dapat memvisualisasikan cluster pada scatterplot yang menampilkan dua komponen utama pertama pada sumbu menggunakan fungsi fivz_cluster() :

 #plot results of final k-means model
fviz_cluster(km, data = df)

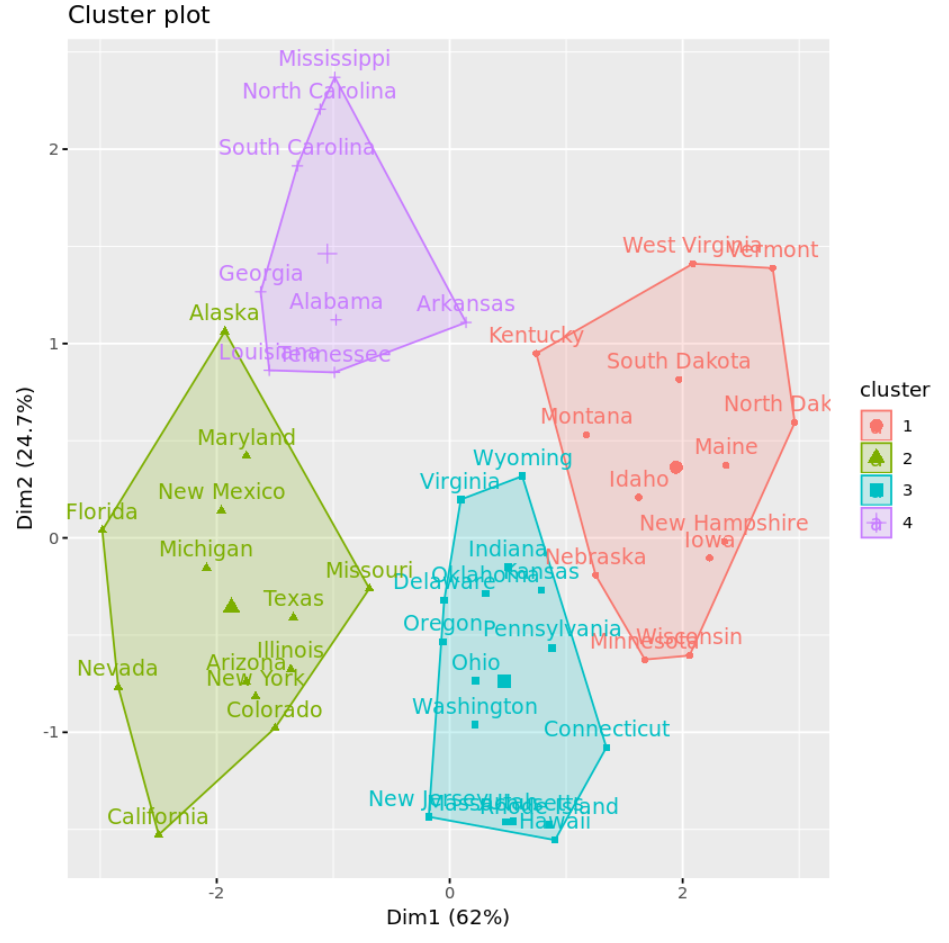
Kita juga dapat menggunakan fungsi Aggregate() untuk mencari rata-rata variabel di setiap cluster:

 #find means of each cluster
aggregate(USArrests, by= list (cluster=km$cluster), mean)

cluster Murder Assault UrbanPop Rape
				
1 3.60000 78.53846 52.07692 12.17692
2 10.81538 257.38462 76.00000 33.19231
3 5.65625 138.87500 73.87500 18.78125
4 13.93750 243.62500 53.75000 21.41250

Kami menafsirkan keluaran ini sebagai berikut:

• Jumlah rata-rata pembunuhan per 100.000 warga di negara-negara bagian Grup 1 adalah 3,6 .
• Jumlah rata-rata penyerangan per 100.000 warga di negara-negara bagian Grup 1 adalah 78,5 .
• Persentase rata-rata penduduk yang tinggal di daerah perkotaan di antara negara bagian Grup 1 adalah 52,1% .
• Jumlah rata-rata pemerkosaan per 100.000 warga di negara-negara bagian Grup 1 adalah 12,2 .

Dan seterusnya.

Kita juga dapat menambahkan penetapan klaster setiap negara bagian ke kumpulan data asli:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = km$cluster)

#view final data
head(final_data)

	Murder Assault UrbanPop Rape cluster
				
Alabama 13.2 236 58 21.2 4
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 4
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Kelebihan dan Kekurangan Clustering K-Means

Pengelompokan K-means menawarkan keuntungan sebagai berikut:

• Ini adalah algoritma yang cepat.
• Itu dapat menangani kumpulan data besar dengan baik.

Namun, ia memiliki potensi kelemahan sebagai berikut:

• Hal ini mengharuskan kita untuk menentukan jumlah cluster sebelum menjalankan algoritma.
• Ini sensitif terhadap outlier.

Dua alternatif pengelompokan k-means adalah pengelompokan k-means dan pengelompokan hierarki.

Anda dapat menemukan kode R lengkap yang digunakan dalam contoh ini di sini .