Cara melakukan regresi linier pada kalkulator ti-84

Regresi linier adalah metode yang dapat kita gunakan untuk memahami hubungan antara variabel penjelas, x, dan variabel respon, y.

Tutorial ini menjelaskan cara melakukan regresi linier pada kalkulator TI-84.

Contoh: regresi linier pada kalkulator TI-84

Misalkan kita ingin memahami hubungan antara jumlah jam belajar siswa untuk suatu ujian dan nilai yang mereka terima pada ujian tersebut.

Untuk mengeksplorasi hubungan ini, kita dapat melakukan langkah-langkah berikut pada kalkulator TI-84 untuk melakukan regresi linier sederhana menggunakan jam belajar sebagai variabel penjelas dan nilai ujian sebagai variabel respon.

Langkah 1: Masukkan datanya.

Pertama, kita akan memasukkan nilai data untuk variabel penjelas dan variabel respon. Tekan Stat lalu tekan EDIT . Masukkan nilai variabel penjelas (jam belajar) berikut pada kolom L1 dan nilai variabel respon (skor ujian) pada kolom L2:

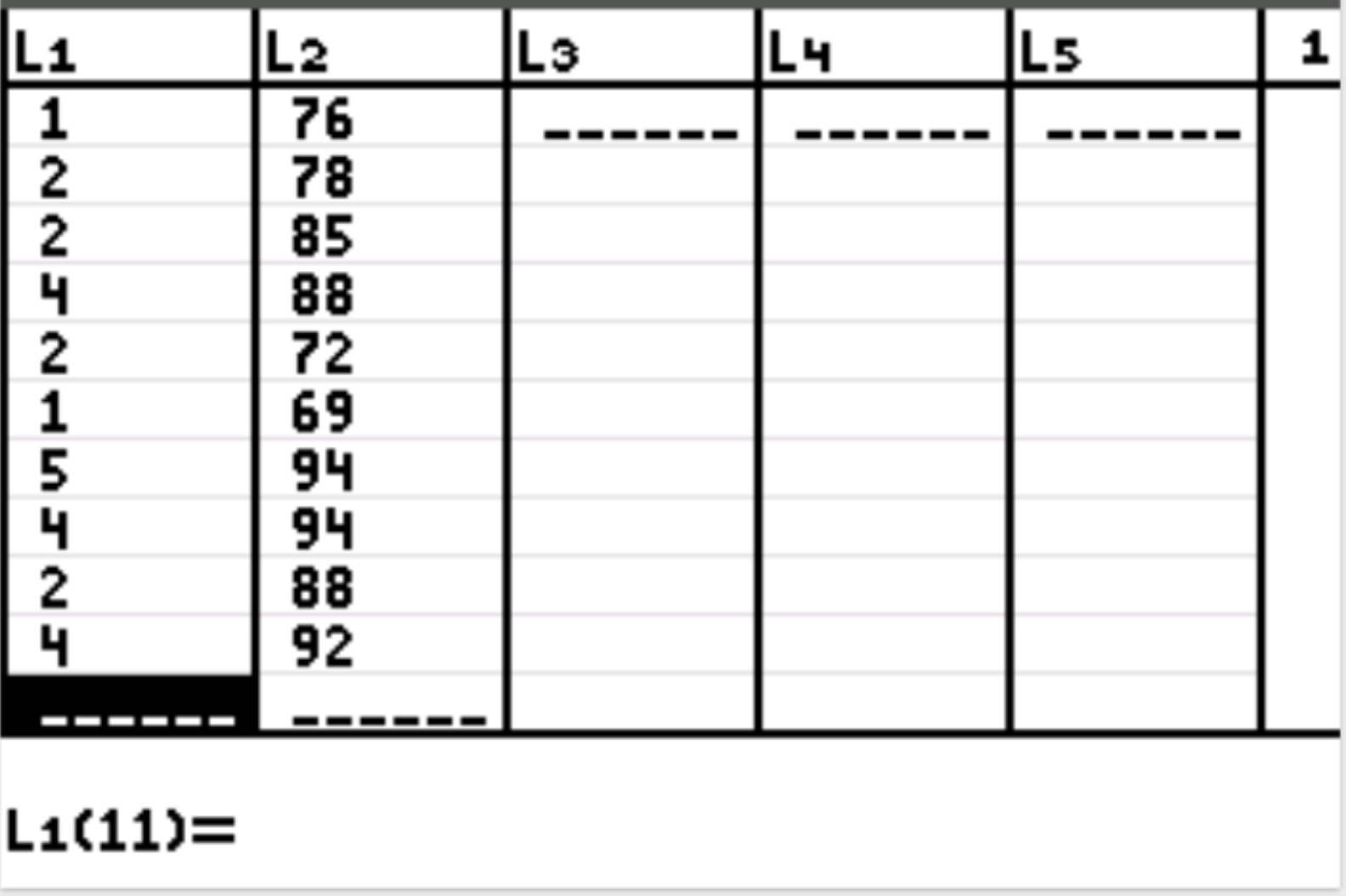
Langkah 2: Lakukan regresi linier.

Selanjutnya kita akan melakukan regresi linier. Tekan Stat lalu gulir ke CALC . Kemudian gulir ke 8: Linreg(a+bx) dan tekan Enter .

Untuk Xlist dan Ylist pastikan L1 dan L2 dipilih karena ini adalah kolom yang kita gunakan untuk memasukkan data kita. Biarkan FreqList kosong. Gulir ke bawah ke Hitung dan tekan Enter . Output berikut akan muncul secara otomatis:

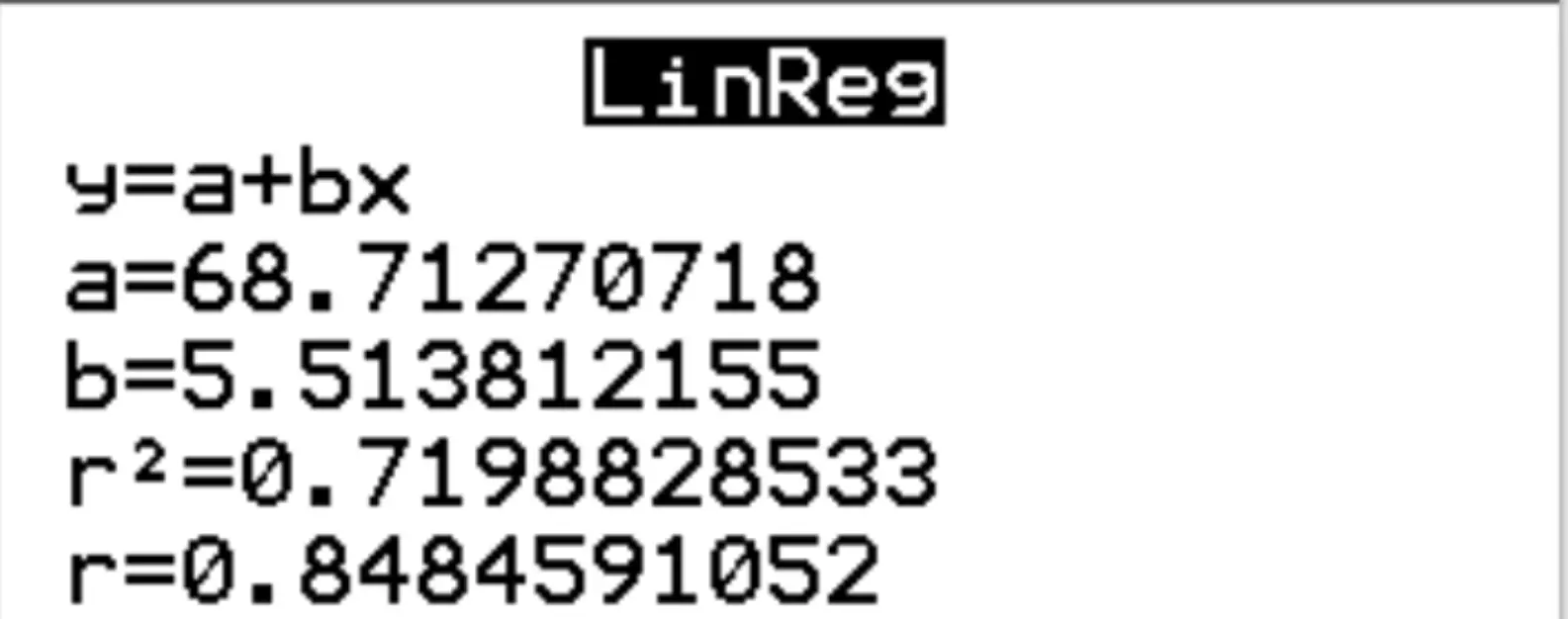
Langkah 3: Interpretasikan hasilnya.

Dari hasil tersebut terlihat bahwa persamaan regresi yang diestimasi adalah:

nilai ujian = 68,7127 + 5,5138*(jam)

Kami menafsirkan koefisien jam berarti bahwa untuk setiap tambahan jam belajar, nilai ujian akan meningkat rata-rata 5,5138 . Kami menafsirkan koefisien intersep sebagai nilai ujian yang diharapkan untuk siswa yang belajar tanpa jam kerja adalah 68,7127 .

Kita dapat menggunakan persamaan regresi perkiraan ini untuk menghitung nilai ujian yang diharapkan seorang siswa, berdasarkan jumlah jam belajar.

Misalnya, seorang siswa yang belajar selama tiga jam harus mencapai nilai ujian 85,25 :

nilai ujian = 68,7127 + 5,5138*(3) = 85,25

Kita juga dapat melihat bahwa r kuadrat untuk model regresi adalah r ² = 0,7199 .

Nilai ini dikenal sebagai koefisien determinasi. Merupakan proporsi varians pada variabel respon yang dapat dijelaskan oleh variabel penjelas. Dalam contoh ini, 71,99% variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar.

Sumber daya tambahan

Cara Membuat Plot Sisa pada Kalkulator TI-84
Cara Melakukan Regresi Kuadrat pada Kalkulator TI-84
Cara Melakukan Regresi Eksponensial pada Kalkulator TI-84
Cara Melakukan Regresi Logaritma pada Kalkulator TI-84