Kapan menggunakan korelasi peringkat spearman (2 skenario)

Cara paling umum untuk mengukur hubungan linier antara dua variabel adalah dengan menggunakan koefisien korelasi Pearson , yang selalu bernilai antara -1 dan 1 dengan:

• -1 menunjukkan korelasi linier negatif sempurna
• 0 menunjukkan tidak ada korelasi linier
• 1 menunjukkan korelasi linier positif sempurna

Namun, jenis koefisien korelasi ini bekerja paling baik bila hubungan mendasar yang sebenarnya antara kedua variabel bersifat linier .

Ada jenis koefisien korelasi lain yang disebut korelasi peringkat Spearman yang paling baik digunakan dalam dua skenario spesifik:

Skenario 1 : Saat bekerja dengan data rahasia.

• Contohnya adalah kumpulan data yang berisi peringkat nilai ujian matematika siswa serta peringkat nilai ujian sains siswa di suatu kelas.

Skenario 2 : Ketika terdapat satu atau lebih outlier ekstrim.

• Jika terdapat outlier ekstrem dalam kumpulan data, koefisien korelasi Pearson akan sangat terpengaruh.

Contoh berikut menunjukkan cara menghitung korelasi peringkat Spearman di setiap skenario.

Skenario 1: Mengkorelasikan Peringkat Spearman dengan Data Peringkat

Pertimbangkan kumpulan data berikut (dan diagram sebar terkait) yang menunjukkan hubungan antara dua variabel:

Dengan menggunakan perangkat lunak statistik, kita dapat menghitung koefisien korelasi berikut untuk kedua variabel ini:

• Korelasi Pearson: 0,79
• Korelasi peringkat Spearman: 1

Dalam skenario ini, jika kita hanya peduli pada peringkat nilai data (saat peringkat x meningkat, apakah peringkat y juga meningkat?), maka korelasi peringkat Spearman akan memberi kita gambaran yang lebih baik tentang korelasi antara kedua variabel tersebut. .

Dalam kumpulan data khusus ini, seiring dengan meningkatnya peringkat x, peringkat y selalu meningkat.

Korelasi peringkat Spearman secara sempurna menangkap perilaku ini dengan memberi tahu kita bahwa terdapat hubungan positif sempurna ( ρ = 1 ) antara peringkat x dan peringkat y.

Di sisi lain, korelasi Pearson menunjukkan bahwa terdapat hubungan linier yang kuat ( r = 0,79 ) antara kedua variabel.

Hal ini memang benar, namun tidak ada gunanya jika kita hanya peduli pada hubungan antara barisan x dan barisan y.

Skenario 2: Korelasi peringkat Spearman dengan outlier ekstrim

Pertimbangkan kumpulan data berikut (dan diagram sebar terkait) yang menunjukkan hubungan antara dua variabel:

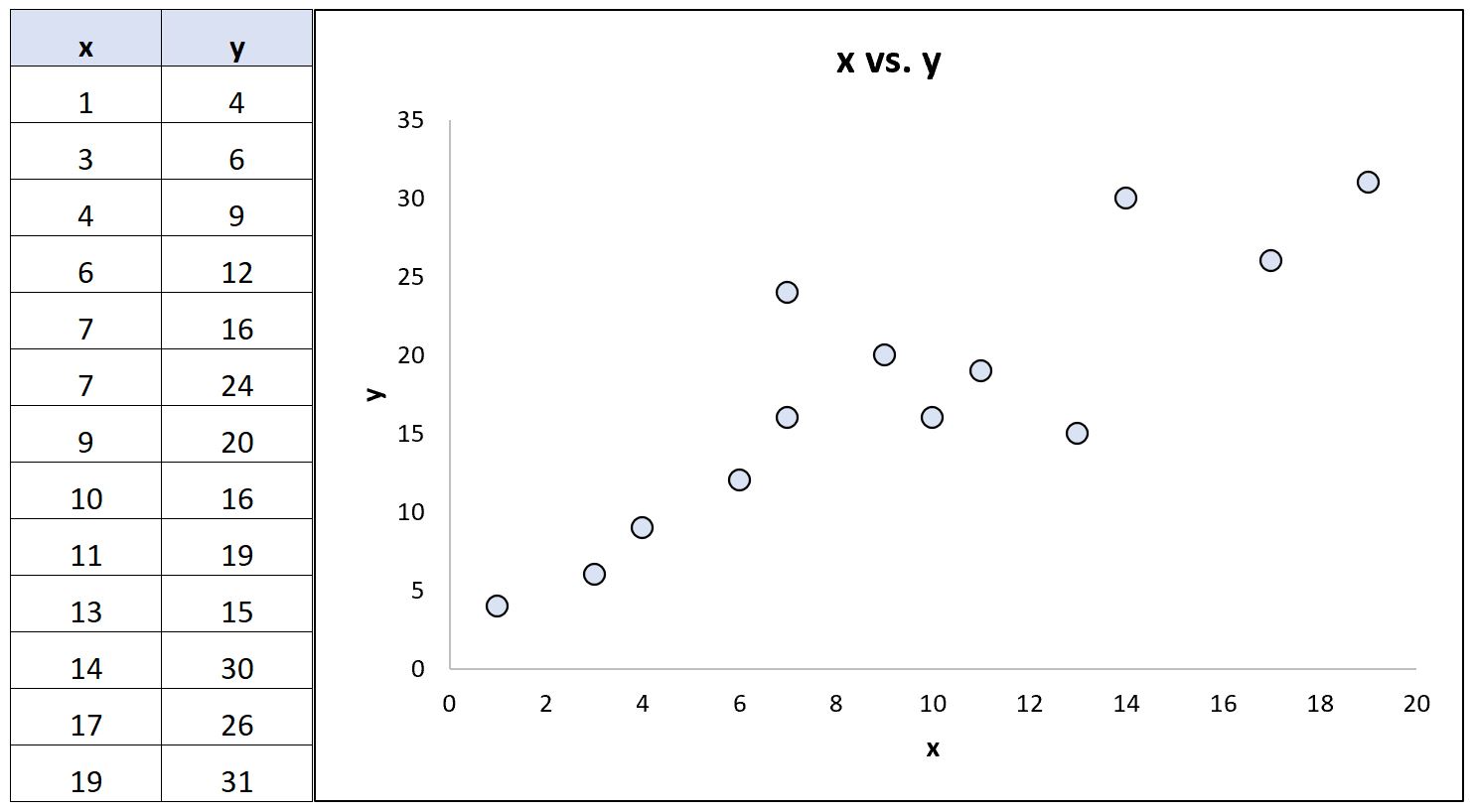
Dengan menggunakan perangkat lunak statistik, kita dapat menghitung koefisien korelasi berikut untuk kedua variabel ini:

• Korelasi Pearson: 0,86
• Korelasi peringkat Spearman: 0,85

Koefisien korelasinya hampir sama karena hubungan mendasar antar variabel mendekati linier dan tidak ada outlier yang ekstrim.

Sekarang misalkan kita mengubah nilai y terakhir dalam dataset sehingga menjadi nilai outlier ekstrim:

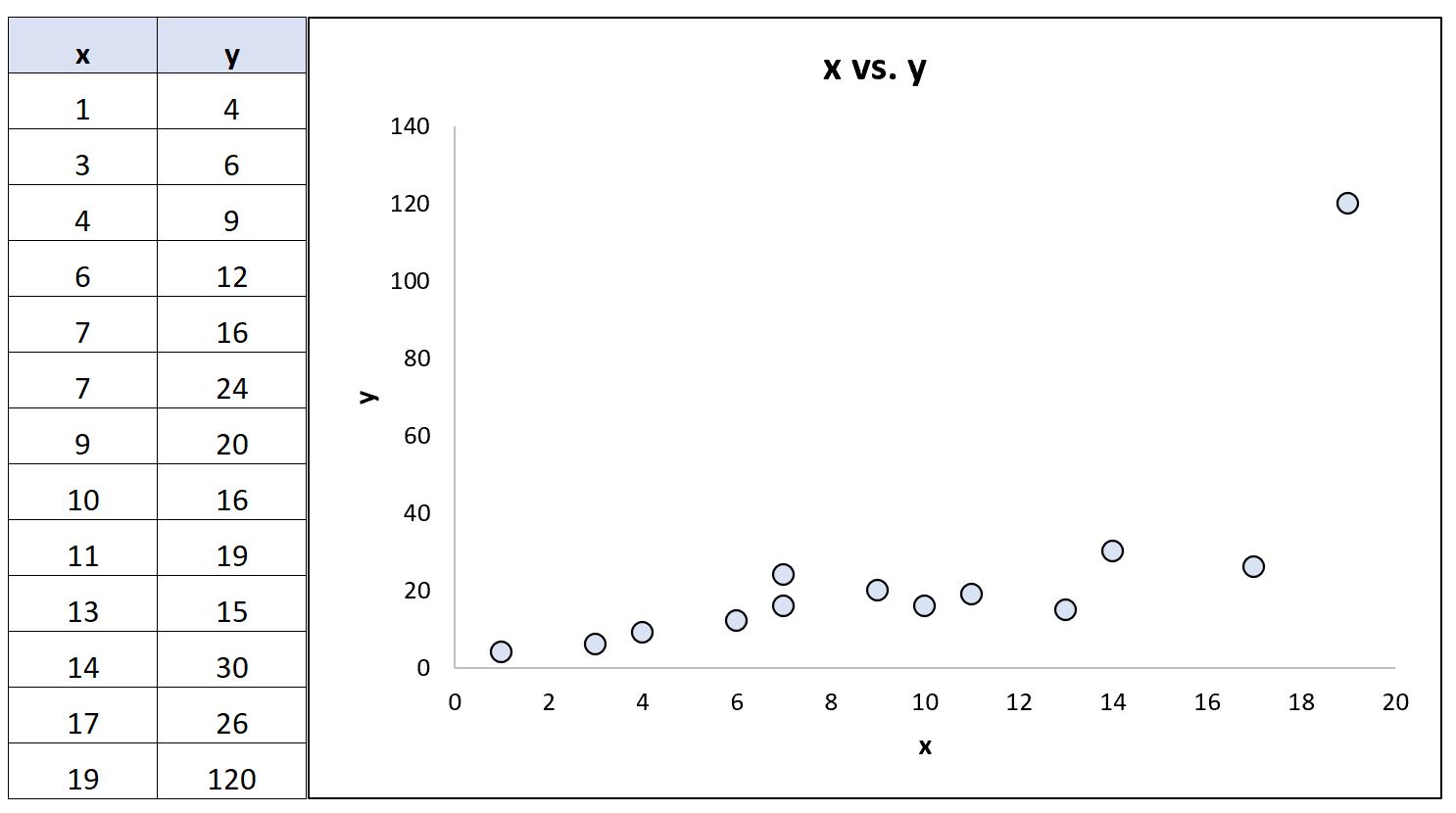
Dengan menggunakan perangkat lunak statistik, kita dapat menghitung ulang koefisien korelasi:

• Korelasi Pearson: 0,69
• Korelasi peringkat Spearman: 0,85

Koefisien korelasi Pearson berubah secara signifikan sedangkan koefisien korelasi peringkat Spearman tetap sama.

Dengan menggunakan jargon statistik, kita dapat mengatakan bahwa hubungan antara x dan y bersifat monotonik (jika x bertambah, y umumnya meningkat) tetapi tidak linier karena outlier sangat mempengaruhi data.

Dalam skenario ini, korelasi peringkat Spearman mengkuantifikasi hubungan monotonik ini dengan baik, sedangkan korelasi Pearson kurang berhasil karena berupaya menghitung hubungan linier antara kedua variabel.

Terkait: Cara Melaporkan Korelasi Peringkat Spearman dalam Format APA

Sumber daya tambahan

Tutorial berikut menjelaskan cara menghitung korelasi peringkat Spearman menggunakan perangkat lunak yang berbeda:

Cara Menghitung Korelasi Rank Spearman di Excel
Cara Menghitung Korelasi Rank Spearman di Google Sheets
Cara menghitung korelasi rank Spearman di R
Cara Menghitung Korelasi Peringkat Spearman dengan Python