Kartu kendali p
Pada artikel ini Anda akan mempelajari apa itu diagram kendali P dan kegunaannya. Kami juga menjelaskan cara membuat diagram kendali P dan, sebagai tambahan, Anda akan dapat melihat latihan diselesaikan langkah demi langkah.
Apa itu peta kendali P?
Bagan kendali P , atau sederhananya bagan P , adalah grafik yang mewakili evolusi proporsi unit yang rusak dan batas kendalinya . Oleh karena itu, peta kendali P adalah peta yang digunakan untuk mengendalikan proporsi unit yang cacat.
Dalam manajemen mutu kita sering kali harus mempelajari apakah dalam suatu proses produksi unit-unit tersebut diproduksi dengan benar atau sebaliknya, apakah terlalu banyak cacat yang terjadi. Dengan demikian, peta kendali P memungkinkan untuk menganalisis evolusi persentase unit cacat dan melihat kapan proses produksi terkendali dan kapan tidak.
Namun peta kendali P tidak hanya digunakan untuk mengendalikan suatu proses produksi, tetapi juga memiliki aplikasi lain seperti mengendalikan proporsi pasien atau mengendalikan tingkat keberhasilan suatu percobaan dikotomis. Meskipun terutama digunakan untuk mengontrol proses produksi.
Salah satu ciri peta kendali P adalah ukuran sampel berbeda yang dianalisis tidak harus sama, sehingga dapat diambil sampel dengan ukuran berbeda untuk melakukan studi statistik.
Singkatnya, peta kendali P memungkinkan kita menganalisis kasus-kasus yang memiliki dua kemungkinan hasil: “sukses” (unit yang diproduksi dengan baik) dan “kegagalan” (unit yang rusak). Artinya, peta kendali P berguna untuk kasus-kasus yang mengikuti distribusi binomial.
Cara Membuat Bagan Kendali P
Untuk membuat diagram kendali P Anda harus mengikuti langkah-langkah berikut:
- Ambil sampel : Pertama-tama, Anda perlu mengambil sampel yang berbeda untuk melihat bagaimana proporsi berubah dalam grafik. Ukuran sampel bisa berbeda-beda, namun disarankan untuk mengambil minimal 20 sampel.
- Hitung proporsi p : Untuk setiap sampel, Anda harus menghitung proporsi individu yang kekurangan.
- Hitung nilai rata-rata proporsi : Dari semua elemen yang dipelajari, Anda perlu menghitung total proporsi unit yang cacat.
- Hitung batas kendali diagram P : Untuk setiap sampel yang diuji, Anda perlu mencari batas kendalinya menggunakan rumus yang diberikan di bawah ini. Perlu diingat bahwa nilai batas kendali akan berbeda-beda jika ukuran setiap sampel berbeda.
- Plot nilai pada grafik : Anda sekarang perlu memplot nilai proporsi sampel yang diperoleh serta batas kendali yang dihitung pada grafik.
- Analisislah peta kendali P : yang terakhir, yang perlu dilakukan hanyalah memeriksa bahwa tidak ada nilai proporsi yang melebihi batas kendali dan oleh karena itu proses terkendali. Jika tidak, tindakan harus diambil untuk memperbaiki proses produksi.
![]()
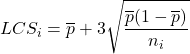
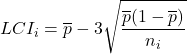
Emas
![]()
Dan
![]()
masing-masing adalah batas kendali atas dan bawah sampel i,
![]()
adalah nilai rata-rata proporsi cacat dan
![]()
adalah ukuran sampel i.
Contoh peta kendali P
Untuk menyelesaikan asimilasi konsep, kita akan melihat contoh penyelesaian pembuatan kartu kendali P.
- Sebuah perusahaan mengumpulkan 25 sampel produk dan mencatat di setiap sampel ukuran sampel dan jumlah suku cadang cacat yang ditemukan. Anda dapat melihat data yang dikumpulkan pada tabel berikut:
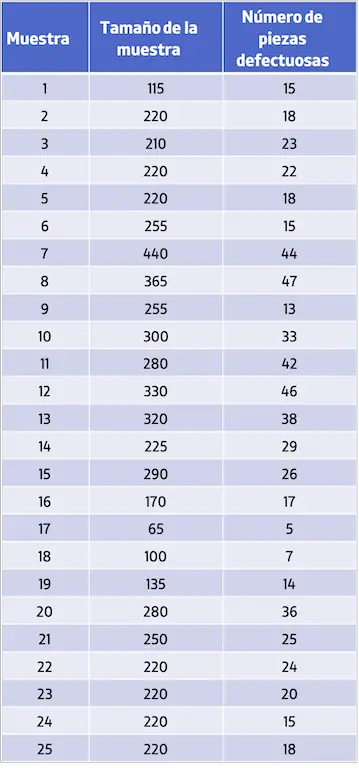
Untuk menghasilkan peta kendali P, pertama-tama perlu dihitung proporsi total unit yang cacat. Untuk melakukan ini, cukup bagi jumlah cacat dengan jumlah unit yang diproduksi:
![]()
Sekarang mari kita hitung proporsi cacat untuk setiap sampel dan batas kendali untuk setiap sampel. Sebagai contoh, kami melanjutkan menghitung sampel pertama:
![]()
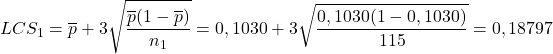
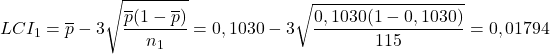
Dengan demikian, proporsi cacat dan batas kendali masing-masing sampel adalah sebagai berikut:
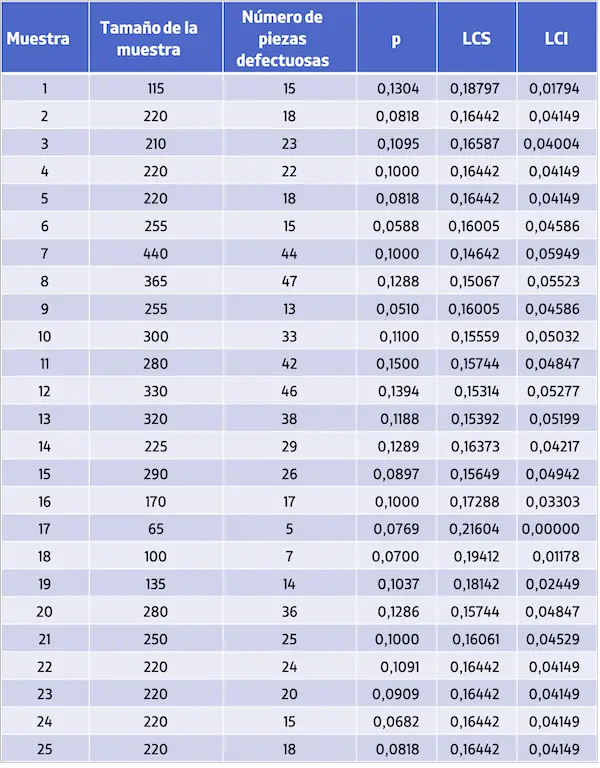
Setelah kita menghitung semua batas kendali, kita merepresentasikan nilai proporsi cacat dan batas kendalinya pada grafik untuk mendapatkan grafik kendali P:
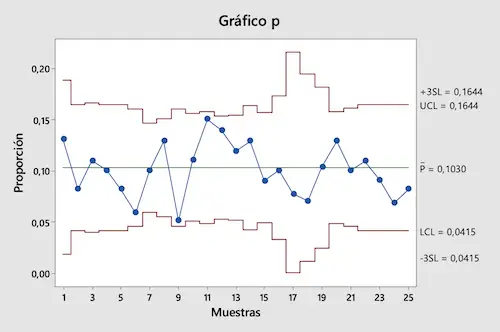
Seperti terlihat dari grafik, semua nilai proporsi berada dalam batas kendali. Oleh karena itu kami menyimpulkan bahwa proses produksi yang diteliti terkendali.
Jenis Bagan Kontrol Lainnya
Bagan P adalah jenis bagan kendali atribut. Bagan kendali atribut lain yang ada meliputi:
- Kartu kendali NP – Berbeda dengan kartu P, proporsi produk cacat tidak dikontrol, melainkan jumlah produk cacat.
- Kartu kendali C : Jumlah kesalahan yang terjadi dipantau.
- Peta kendali U : Jumlah cacat dikontrol seperti pada bagan C, tetapi ukuran sampelnya bervariasi.