Kemungkinan perpotongan peristiwa

Artikel ini menjelaskan cara menghitung peluang perpotongan kejadian. Jadi, Anda akan mengetahui apa rumus probabilitas perpotongan kejadian dan, sebagai tambahan, latihan yang diselesaikan langkah demi langkah.

Apa titik potong peristiwa?

Dalam teori probabilitas, perpotongan kejadian adalah suatu operasi kejadian yang hasilnya terdiri dari kejadian-kejadian dasar yang sama dengan semua kejadian dalam operasi tersebut. Artinya, perpotongan kejadian A dan B dibentuk oleh semua kejadian yang terjadi pada A dan B pada waktu yang sama.

Perpotongan dua kejadian dinyatakan dengan simbol ⋂. Jadi, perpotongan kejadian A dan B ditulis A⋂B.

Misalnya, dalam percobaan acak pelemparan sebuah dadu, jika salah satu kejadian adalah pelemparan bilangan genap A={2, 4, 6} dan kejadian lainnya adalah pelemparan bilangan lebih dari tiga B={4, 5, 6 }, titik potong kedua kejadian tersebut adalah A⋂B={4, 6}.

Rumus peluang perpotongan kejadian

Peluang perpotongan dua kejadian sama dengan peluang terjadinya satu kejadian dikalikan peluang bersyarat terjadinya kejadian lain jika diketahui kejadian pertama.

Oleh karena itu, rumus peluang perpotongan dua kejadian adalah P(A⋂B)=P(A) P(B|A)=P(B) P(A|B).

Emas:

• 

  Dan

  

  Ini adalah dua peristiwa yang bergantung.

• 

  adalah peluang perpotongan kejadian A dan kejadian B.

• 

  adalah peluang terjadinya kejadian A.

• 

  adalah peluang bersyarat terjadinya peristiwa B jika terjadi peristiwa A.

• 

  adalah peluang terjadinya kejadian B.

• 

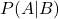
  adalah probabilitas bersyarat dari kejadian A yang terjadi pada kejadian tertentu B.

Namun, jika kedua peristiwa tersebut saling bebas, berarti peluang terjadinya suatu peristiwa tidak bergantung pada terjadinya peristiwa yang lain. Oleh karena itu, rumus peluang perpotongan dua kejadian independen adalah sebagai berikut:

Emas:

• 

  Dan

  

  Ini adalah dua peristiwa independen.

• 

  adalah peluang perpotongan kejadian kejadian A dan kejadian B.

• 

  adalah peluang terjadinya kejadian A.

• 

  adalah peluang terjadinya kejadian B.

Contoh nyata probabilitas perpotongan peristiwa

Selanjutnya, kami memberikan kepada Anda dua contoh yang diselesaikan langkah demi langkah sehingga Anda dapat melihat bagaimana probabilitas perpotongan dua peristiwa dihitung. Pertama-tama kita akan melihat contoh perpotongan dua kejadian independen dan kemudian dua kejadian dependen, sehingga Anda dapat melihat kedua kasus tersebut.

Peluang perpotongan dua kejadian yang saling bebas

• Hasil imbang diluncurkan tiga kali berturut-turut. Temukan peluang mendapatkan keunggulan pada ketiga pelemparan tersebut.

Dalam hal ini, kejadian-kejadian yang ingin kita hitung probabilitas gabungannya adalah independen, karena hasil pengundian tidak bergantung pada hasil yang diperoleh pada pengundian sebelumnya. Oleh karena itu, untuk menentukan peluang munculnya tiga gambar berturut-turut, kita harus menggunakan rumus peluang perpotongan untuk kejadian-kejadian independen:

Jika diundi, hanya ada dua kemungkinan hasil, kita bisa mendapatkan kepala atau ekor. Oleh karena itu, peluang munculnya kepala atau ekor pada pelemparan sebuah uang logam adalah:

Jadi, untuk mencari peluang munculnya gambar pada ketiga pelemparan koin, kita perlu mengalikan peluang munculnya gambar dengan tiga:

Singkatnya, kemungkinan mendapatkan gambar tiga kali berturut-turut adalah 12,5%.

Probabilitas perpotongan dua kejadian saling bergantung

• Dalam kotak kosong kita masukkan 8 bola biru, 4 bola oranye, dan 2 bola hijau. Jika kita mengambil satu bola terlebih dahulu kemudian bola yang lain tanpa memasukkan kembali bola pertama ke dalam kotak, berapakah peluang terambilnya bola pertama berwarna biru dan bola kedua berwarna jingga?

Dalam hal ini, kejadiannya bergantung, karena peluang terambilnya bola oranye pada pengambilan kedua bergantung pada warna bola yang diambil pada pengambilan pertama. Oleh karena itu, untuk menghitung probabilitas yang ditanyakan oleh soal kepada kita, kita harus menggunakan rumus probabilitas perpotongan untuk kejadian-kejadian dependen:

Peluang terambilnya bola biru pada pengambilan pertama mudah untuk ditentukan, cukup bagi jumlah bola biru dengan jumlah bola:

Sebaliknya, peluang terambilnya bola oranye setelah pengambilan bola biru dihitung secara berbeda karena jumlah bola oranye berbeda dan, sebagai tambahan, sekarang ada satu bola yang lebih sedikit di dalam kotak:

Jadi, peluang terambilnya bola biru terlebih dahulu kemudian bola oranye dihitung dengan mengalikan dua peluang di atas:

Properti Persimpangan Peristiwa

Dalam teori probabilitas, perpotongan peristiwa memiliki sifat-sifat berikut:

• Sifat komutatif: Urutan kejadian perpotongan tidak mengubah hasil operasi.

• Properti asosiatif: Perpotongan tiga peristiwa dapat dihitung dalam urutan apa pun, karena hasilnya sama.

• Sifat distributif: perpotongan peristiwa memenuhi sifat distributif pada gabungan peristiwa.