Kendall's tau: definisi + contoh

Dalam statistik, korelasi mengacu pada kekuatan dan arah hubungan antara dua variabel. Nilai koefisien korelasi dapat berkisar antara -1 hingga 1, dengan -1 menunjukkan hubungan negatif sempurna, 0 menunjukkan tidak ada hubungan, dan 1 menunjukkan hubungan positif sempurna.

Koefisien korelasi yang paling umum digunakan adalah koefisien korelasi Pearson , yang mengukur hubungan linier antara dua variabel numerik.

Koefisien korelasi yang kurang umum digunakan adalah Kendall’s Tau , yang mengukur hubungan antara dua kolom data yang diberi peringkat.

Rumus menghitung Kendall’s Tau yang sering disingkat τ adalah sebagai berikut:

τ = (CD) / (C+D)

Emas:

C = banyaknya pasangan yang cocok

D = banyaknya pasangan sumbang

Contoh berikut mengilustrasikan cara menggunakan rumus ini untuk menghitung koefisien korelasi peringkat Kendall’s Tau untuk dua kolom data peringkat.

Contoh penghitungan Kendall’s Tau

Diasumsikan dua pelatih bola basket memberi peringkat 12 pemainnya dari yang terburuk hingga yang terbaik. Tabel berikut menunjukkan peringkat yang diberikan masing-masing pelatih kepada para pemainnya:

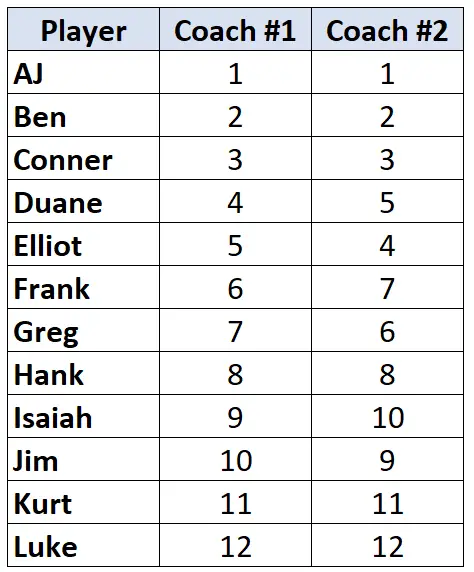
Karena kita bekerja dengan dua kolom data peringkat, maka wajar jika menggunakan Kendall’s Tau untuk menghitung korelasi antara peringkat kedua pelatih. Ikuti langkah-langkah berikut untuk menghitung Kendall’s Tau:

Langkah 1: Hitung jumlah pasangan yang cocok.

Lihat saja peringkat pelatih #2. Dimulai dari pemain pertama, hitung berapa pangkat di bawahnya yang lebih tinggi . Misalnya ada 11 angka di bawah “1” yang lebih besar, maka kita tuliskan 11:

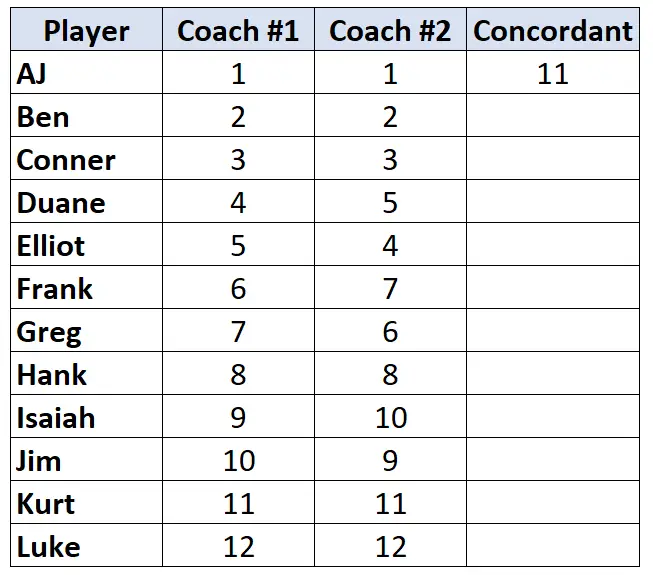
Pindah ke pemain berikutnya dan ulangi prosesnya. Ada 10 angka di bawah “2” yang lebih besar, jadi kita tulis 10:

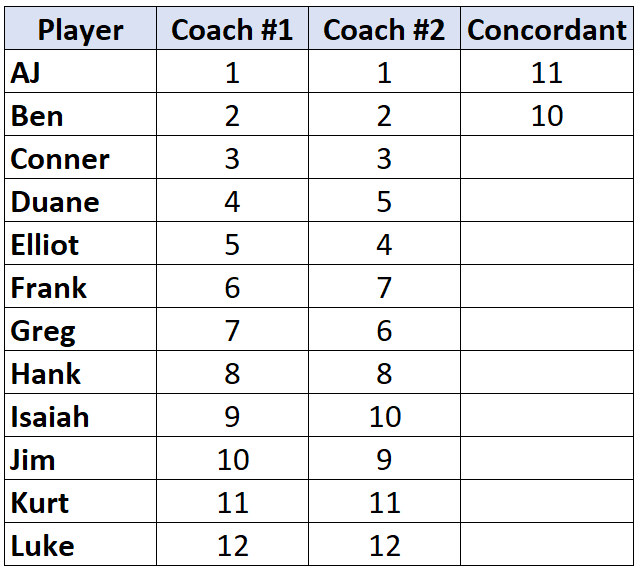
Saat kami mencapai pemain yang peringkatnya lebih rendah dari pemain sebelumnya, dia akan diberi nilai yang sama dengan pemain sebelumnya. Misalnya, Elliot memiliki peringkat “4” yang lebih rendah dari peringkat pemain sebelumnya “5” sehingga ia hanya diberi nilai yang sama dengan pemain sebelumnya:

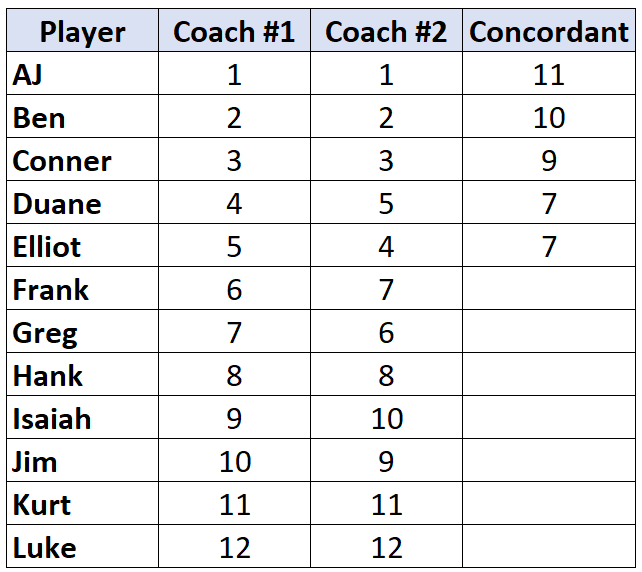
Ulangi proses ini untuk semua pemain:

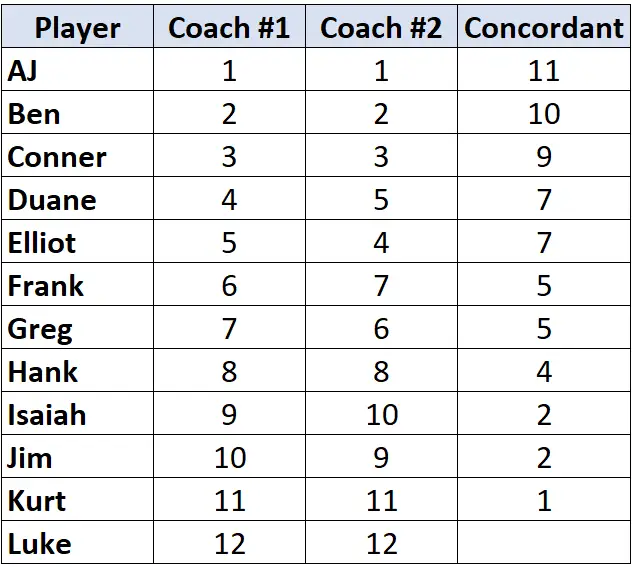
Langkah 2: Hitung jumlah pasangan sumbang.

Sekali lagi, lihat saja peringkat Pelatih #2. Untuk setiap pemain, hitung berapa peringkat di bawahnya yang lebih kecil . Misalnya, Pelatih #2 memberi AJ peringkat “1” dan tidak ada pemain di bawahnya yang memiliki peringkat lebih rendah. Jadi, kami memberinya nilai 0:

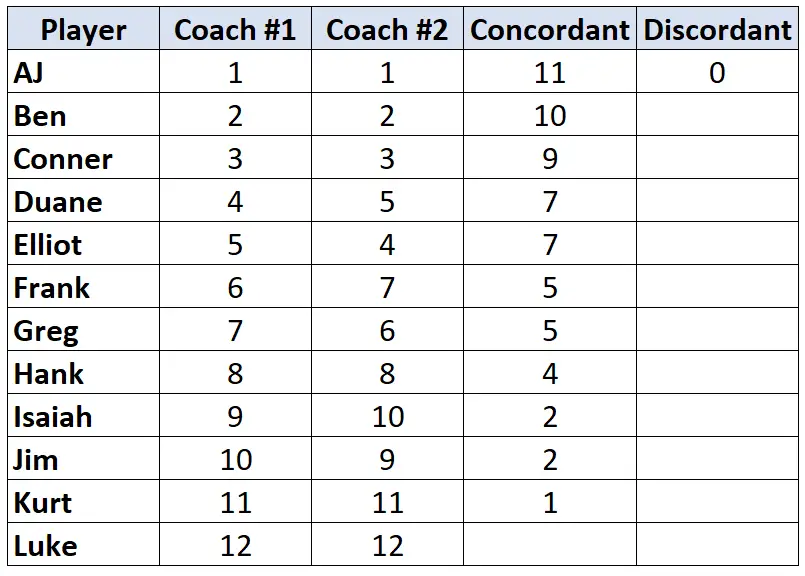
Ulangi proses ini untuk setiap pemain:

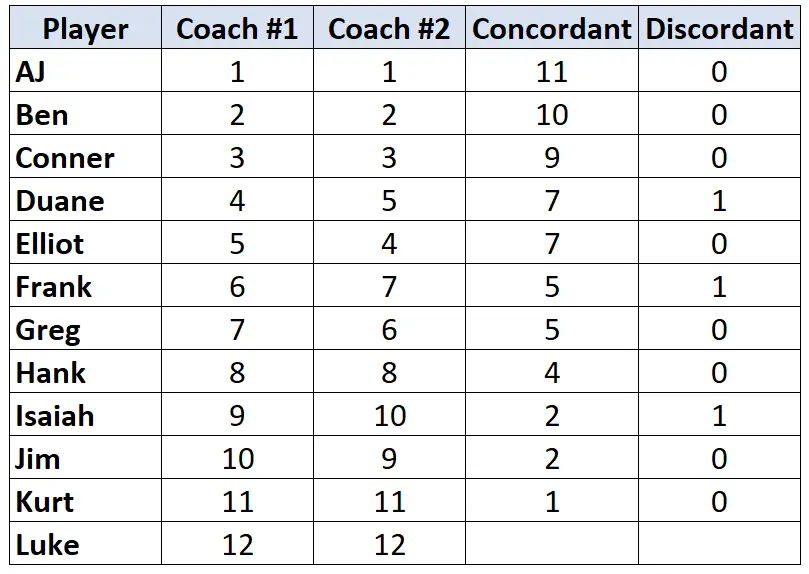
Langkah 3: Hitung jumlah setiap kolom dan temukan Tau Kendall.

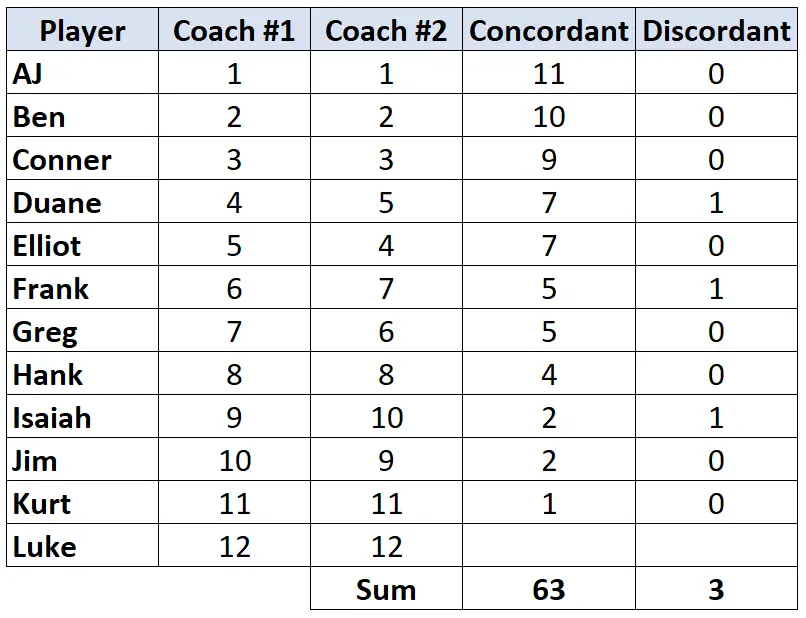
Tau Kendall = (CD) / (C+D) = (63-3) / (63+3) = (60/66) = 0,909 .

Pentingnya statistik Kendall’s Tau

Jika Anda memiliki lebih dari n=10 pasang, Kendall’s Tau umumnya mengikuti distribusi normal. Anda dapat menggunakan rumus berikut untuk menghitung skor-z untuk Kendall’s Tau:

z = 3τ*√ n(n-1) / √ 2(2n+5)

Emas:

τ = nilai yang Anda hitung untuk Kendall’s Tau

n = jumlah pasangan

Berikut cara menghitung z pada contoh sebelumnya:

z = 3(.909)*√ 12(12-1) / √ 2(2*12+5) = 4.11 .

Dengan menggunakan kalkulator skor-Z nilai-P, kita melihat bahwa nilai-p untuk skor-z ini adalah 0,00004 , yang secara statistik signifikan pada tingkat alfa 0,05. Dengan demikian, terdapat korelasi yang signifikan secara statistik antara peringkat yang diberikan kedua pelatih kepada para pemainnya.

Bonus: Cara menghitung Kendall’s Tau di R

Dalam perangkat lunak statistik R, Anda dapat menggunakan fungsi kendall.tau() dari perpustakaan VGAM untuk menghitung Tau Kendall untuk dua vektor, yang menggunakan sintaks berikut:

kendall.tau(x, y)

dimana x dan y adalah dua vektor digital yang sama panjang.

Kode berikut mengilustrasikan cara menghitung Kendall’s Tau untuk data persis yang kita gunakan pada contoh sebelumnya:

 #load VGAM
library(VGAM)

#create vector for each coach's rankings
coach_1 <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12)
coach_2 <- c(1, 2, 3, 5, 4, 7, 6, 8, 10, 9, 11, 12)

#calculate Kendall's Tau
kendall.tau(coach_1, coach_2)

#[1] 0.9090909

Perhatikan bagaimana nilai Tau Kendall cocok dengan nilai yang kita hitung secara manual.