Cara menghitung root mean square error (rmse) di excel

Dalam statistik, analisis regresi adalah teknik yang kita gunakan untuk memahami hubungan antara variabel prediktor, x, dan variabel respon, y.

Saat kita melakukan analisis regresi, kita mendapatkan model yang memberi tahu kita nilai prediksi variabel respon berdasarkan nilai variabel prediktor.

Salah satu cara untuk menilai seberapa cocok model kita dengan kumpulan data tertentu adalah dengan menghitung mean squared error , yang merupakan metrik yang memberi tahu kita seberapa jauh rata-rata nilai prediksi kita dari nilai observasi.

Rumus untuk mencari mean square error yang lebih dikenal dengan RMSE adalah:

RMSE = √[ Σ(P _i – O _i ) ² / n ]

Emas:

• Σ adalah simbol mewah yang berarti “jumlah”
• P _i adalah nilai prediksi observasi ^ke-i dalam dataset
• O _i adalah nilai observasi untuk observasi ^ke-i dalam kumpulan data
• n adalah ukuran sampel

Catatan teknis :

• Kesalahan kuadrat rata-rata dapat dihitung untuk semua jenis model yang menghasilkan nilai prediksi, yang kemudian dapat dibandingkan dengan nilai observasi dari kumpulan data.
• Mean square error kadang juga disebut mean square deviasi, yang sering disingkat RMSD.

Selanjutnya, mari kita lihat contoh cara menghitung mean square error di Excel.

Cara Menghitung Mean Square Error di Excel

Tidak ada fungsi bawaan untuk menghitung RMSE di Excel, tapi kita bisa menghitungnya dengan cukup mudah hanya dengan satu rumus. Kami akan menunjukkan cara menghitung RMSE untuk dua skenario berbeda.

skenario 1

Dalam sebuah skenario, Anda dapat memiliki satu kolom berisi nilai prediksi dari model Anda dan kolom lain berisi nilai observasi. Gambar di bawah menunjukkan contoh skenario ini:

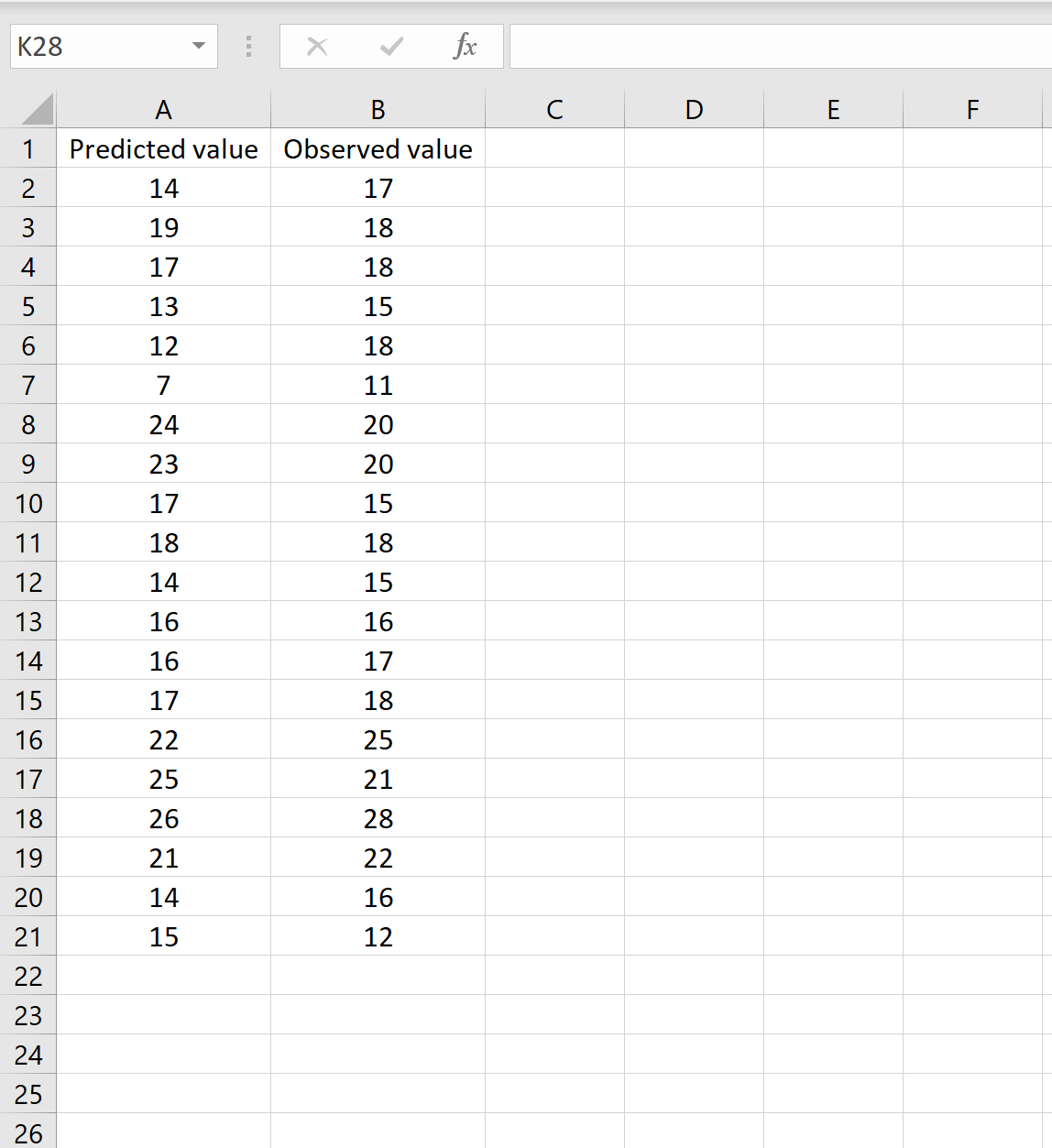
Jika demikian, Anda dapat menghitung RMSE dengan mengetikkan rumus berikut di sel mana pun lalu mengklik CTRL+SHIFT+ENTER:

=SQRT(JUMLAHQ(A2:A21-B2:B21) / JUMLAH(A2:A21))

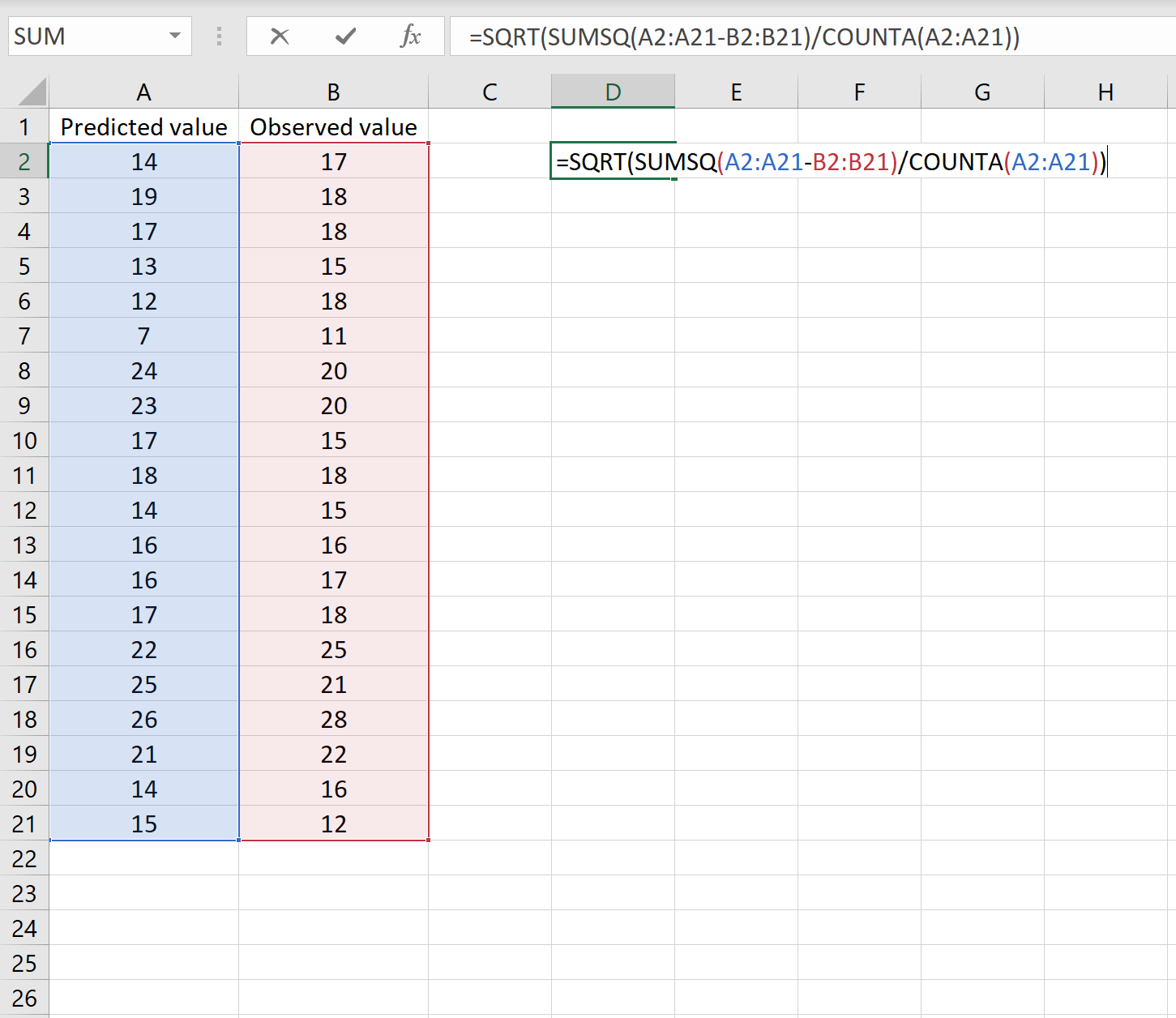
Ini memberitahu kita bahwa kesalahan kuadrat rata-rata adalah 2,6646 .

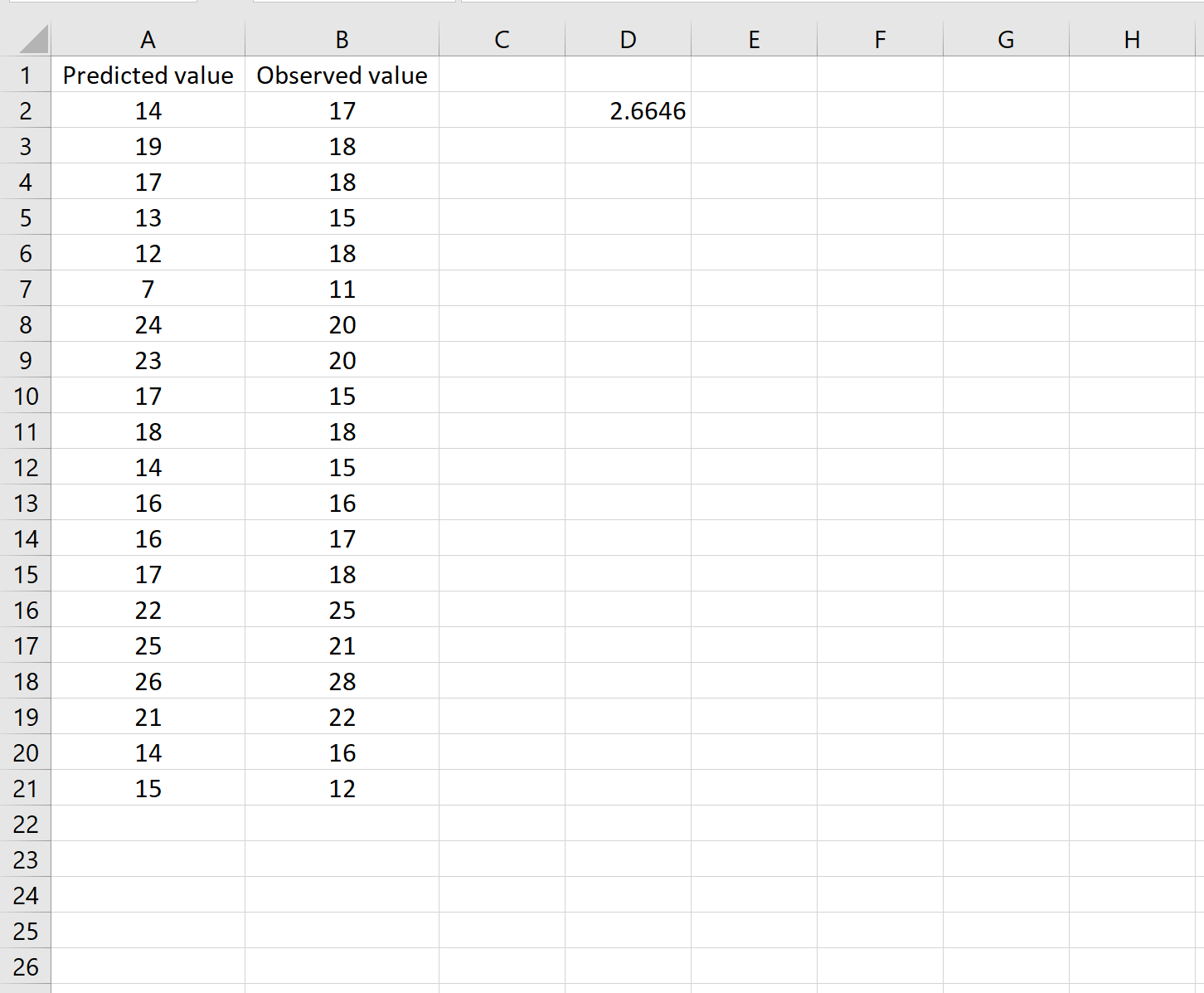
Rumusnya mungkin tampak sedikit rumit, tetapi masuk akal setelah Anda menguraikannya:

= SQRT( JUMLAHQ(A2:A21-B2:B21) / JUMLAH(A2:A21) )

• Pertama, kita menghitung jumlah kuadrat selisih antara nilai prediksi dan nilai observasi menggunakan fungsi SUMSQ() .
• Selanjutnya, kita membaginya dengan ukuran sampel kumpulan data menggunakan COUNTA() , yang menghitung jumlah sel dalam rentang yang tidak kosong.
• Terakhir, kita mengambil akar kuadrat dari keseluruhan perhitungan menggunakan fungsi SQRT() .

Skenario 2

Dalam skenario lain, Anda mungkin sudah menghitung perbedaan antara nilai prediksi dan nilai observasi. Dalam hal ini Anda hanya akan memiliki satu kolom yang menunjukkan perbedaannya.

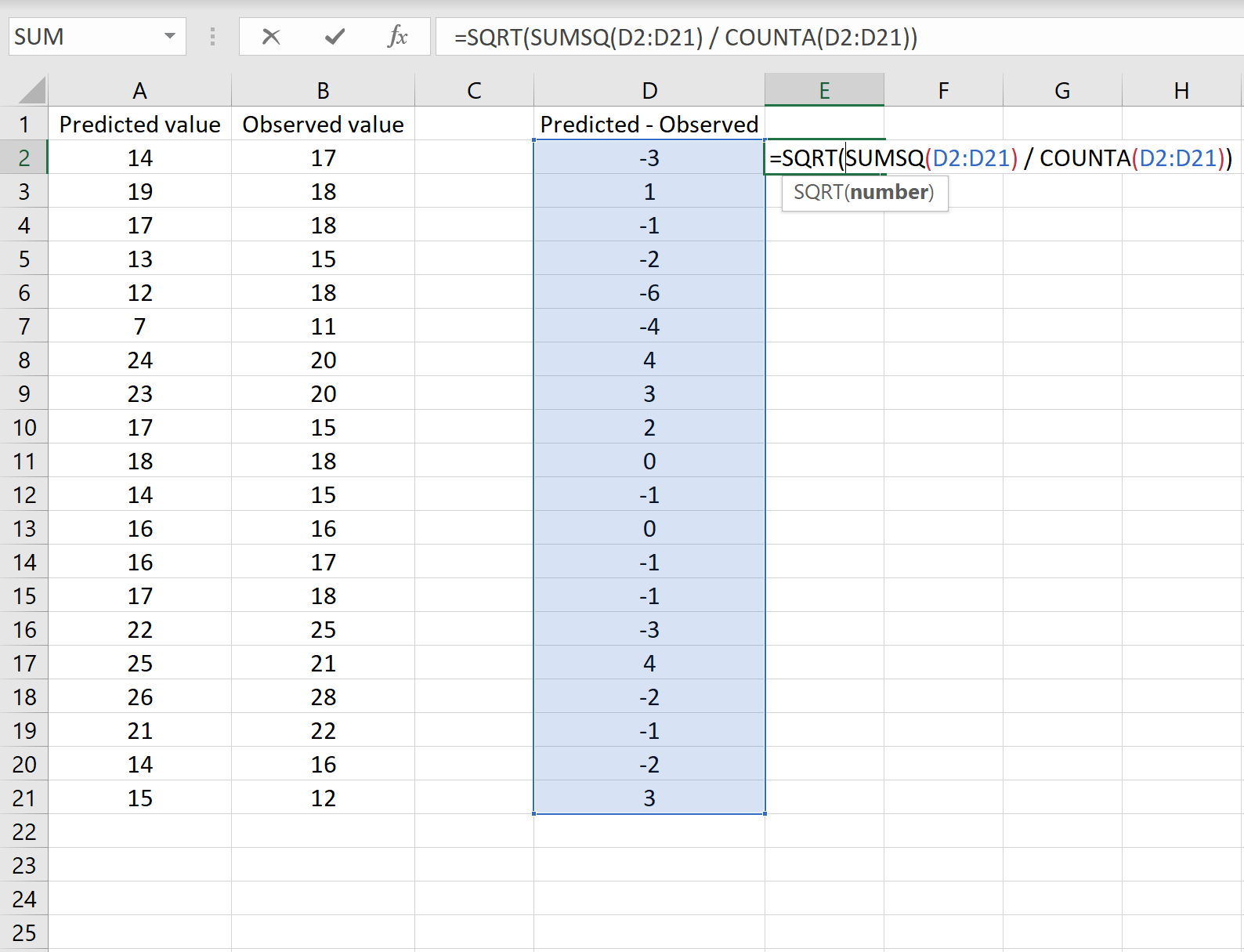
Gambar di bawah menunjukkan contoh skenario ini. Nilai prediksi ditampilkan di kolom A, nilai observasi di kolom B, dan selisih antara nilai prediksi dan nilai observasi di kolom D:

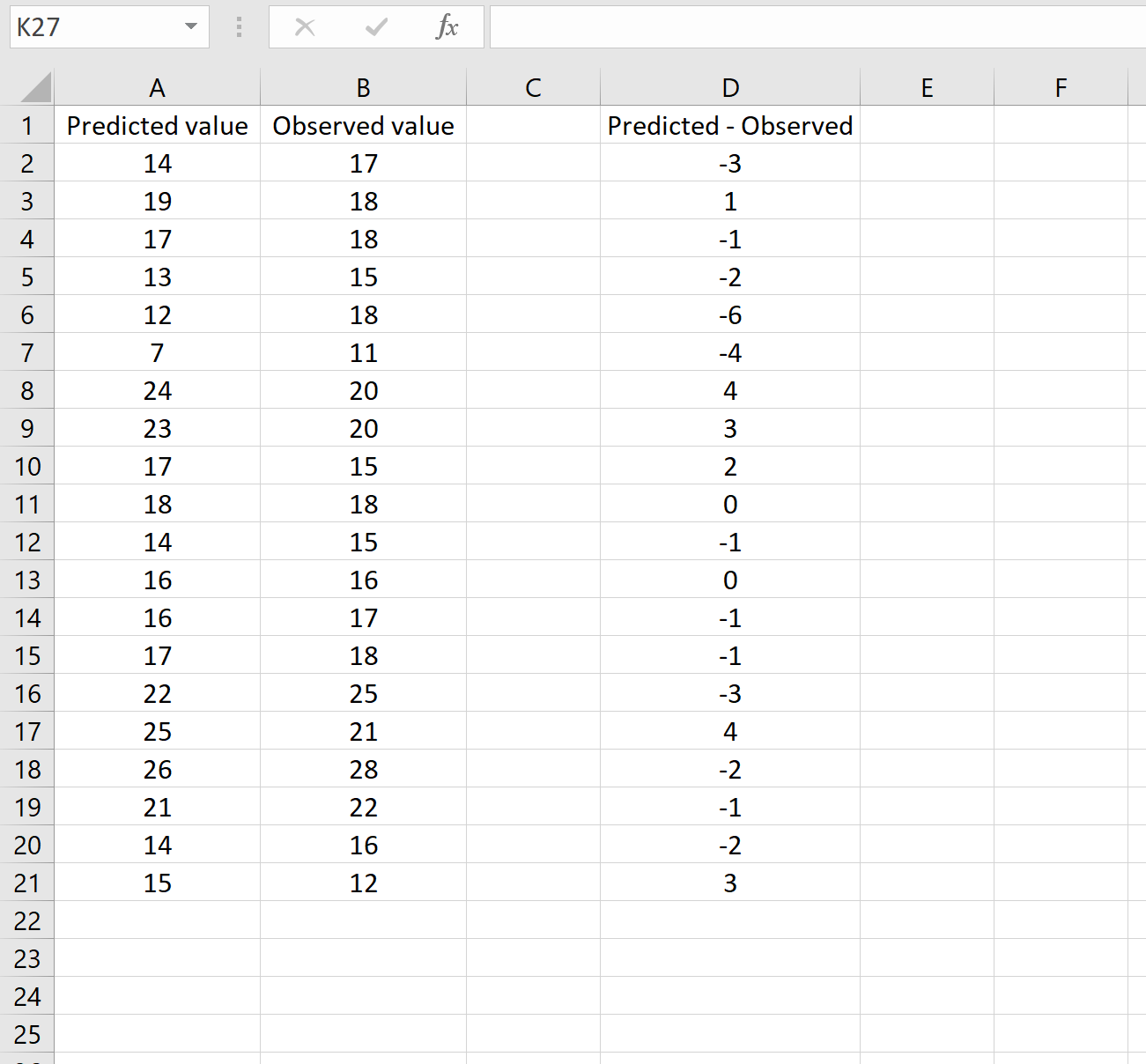
Jika demikian, Anda dapat menghitung RMSE dengan mengetikkan rumus berikut di sel mana pun lalu mengklik CTRL+SHIFT+ENTER:

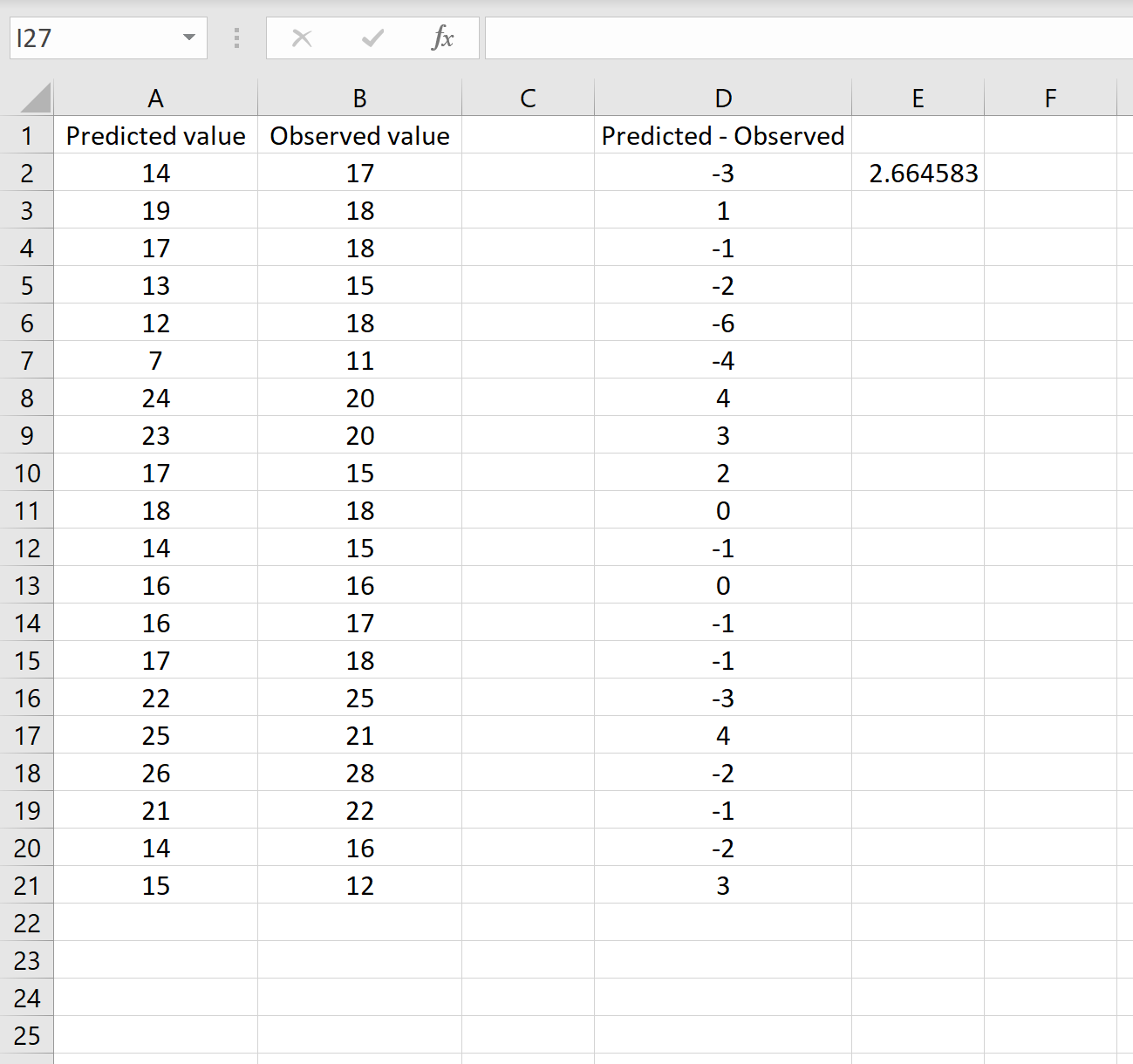
=SQRT(JUMLAHQ(D2:D21) / JUMLAH(D2:D21))

Ini memberitahu kita bahwa kesalahan kuadrat rata-rata adalah 2,6646 , yang sesuai dengan hasil yang diperoleh pada skenario pertama. Hal ini menegaskan bahwa kedua pendekatan untuk menghitung RMSE adalah setara.

Rumus yang kami gunakan pada skenario ini hanya sedikit berbeda dengan rumus yang kami gunakan pada skenario sebelumnya:

= SQRT( JUMLAHQ(D2:D21) / JUMLAH(D2:D21) )

• Karena kita telah menghitung selisih antara nilai prediksi dan nilai observasi di kolom D, kita dapat menghitung jumlah selisih kuadrat menggunakan fungsi SUMSQ().   fungsi hanya dengan nilai dari kolom D.
• Selanjutnya, kita membaginya dengan ukuran sampel kumpulan data menggunakan COUNTA() , yang menghitung jumlah sel dalam rentang yang tidak kosong.
• Terakhir, kita mengambil akar kuadrat dari keseluruhan perhitungan menggunakan fungsi SQRT() .

Bagaimana menafsirkan RMSE

Seperti disebutkan sebelumnya, RMSE adalah cara yang berguna untuk melihat seberapa baik model regresi (atau model apa pun yang menghasilkan nilai prediksi) mampu “menyesuaikan” kumpulan data.

Semakin besar RMSE, semakin besar perbedaan antara nilai prediksi dan observasi, yang berarti semakin buruk kecocokan model regresi dengan data. Sebaliknya, semakin kecil RMSE, maka model tersebut semakin mampu menyesuaikan dengan data.

Akan sangat berguna jika membandingkan RMSE dari dua model berbeda untuk melihat model mana yang paling sesuai dengan data.

Untuk tutorial lebih lanjut di Excel, pastikan untuk memeriksa halaman Panduan Excel kami, yang mencantumkan semua tutorial Excel tentang statistik.