Ketidaksamaan bray-curtis: definisi & contoh

Dinamakan setelah J. Roger Bray dan John Thomas Curtis , ketidaksamaan Bray–Curtis adalah cara mengukur ketidaksamaan antara dua situs berbeda.

Hal ini sering digunakan dalam ekologi dan biologi untuk mengukur perbedaan antara dua lokasi dalam kaitannya dengan spesies yang ditemukan di lokasi tersebut.

Ketidaksamaan Bray-Curtis dihitung sebagai berikut:

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

Emas:

• C _ij : Jumlah nilai terendah untuk spesies yang ditemukan pada setiap lokasi.
• S _i : Jumlah seluruh benda uji yang dihitung di lokasi i
• S _j : Jumlah seluruh benda uji yang dihitung di lokasi j

Ketidaksamaan Bray-Curtis selalu antara 0 dan 1 dimana:

• 0 menunjukkan bahwa dua situs tidak memiliki perbedaan. Dengan kata lain, mereka mempunyai jumlah yang sama persis untuk setiap jenis spesies.
• 1 menunjukkan bahwa dua situs memiliki ketidaksamaan total. Dengan kata lain, mereka tidak berbagi spesies apa pun dengan tipe yang sama.

Contoh berikut menunjukkan cara menghitung ketidaksamaan Bray-Curtis untuk dua lokasi.

Contoh: perhitungan ketidaksamaan Bray-Curtis

Misalkan seorang ahli botani keluar dan menghitung jumlah lima spesies tumbuhan berbeda (A, B, C, D, dan E) di dua lokasi berbeda.

Tabel berikut merangkum data yang dia kumpulkan:

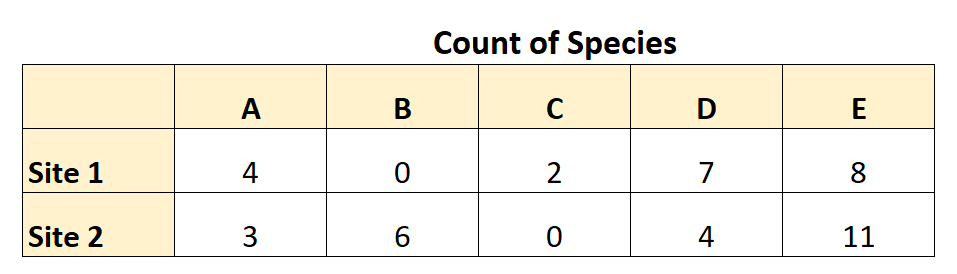
Dengan menggunakan data ini, dia dapat menghitung ketidaksamaan Bray-Curtis sebagai berikut:

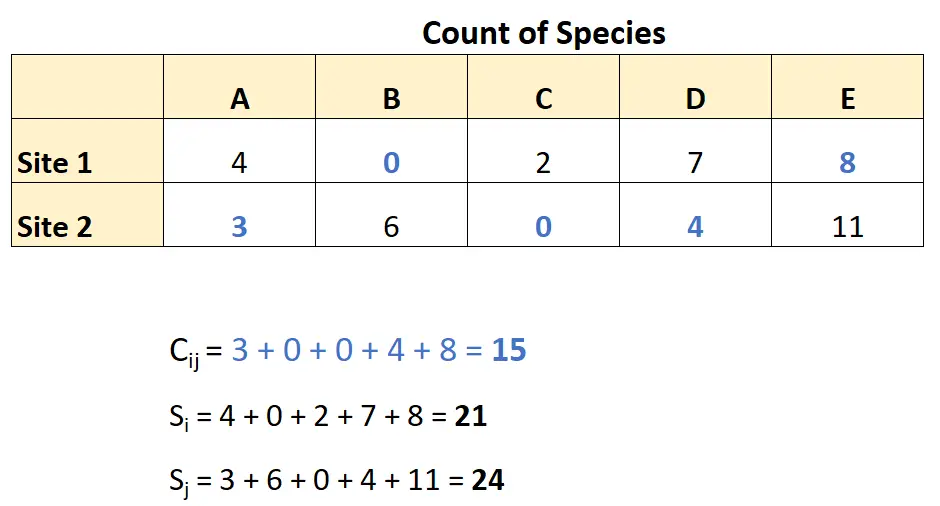
Dengan mengintegrasikan angka-angka ini ke dalam rumus ketidaksamaan Bray-Curtis, kita memperoleh:

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• SM _ij = 0,33

Ketidaksamaan Bray-Curtis antara kedua situs ini adalah 0,33 .

Asumsi utama ketidaksamaan Bray-Curtis

Ketidaksamaan Bray-Curtis mengasumsikan bahwa kedua situs tersebut berukuran sama.

Ini adalah asumsi yang sangat penting karena jika satu lokasi berukuran empat kali lebih besar dibandingkan lokasi lainnya, secara alami kita akan memiliki lebih banyak spesies di lokasi yang lebih besar dibandingkan di lokasi yang lebih kecil, karena terdapat lebih banyak wilayah yang dapat dicakup.

Untuk mengilustrasikan hal ini, misalkan salah satu lokasi yang datanya dikumpulkan oleh ahli botani berukuran empat kali lebih besar dibandingkan lokasi lainnya:

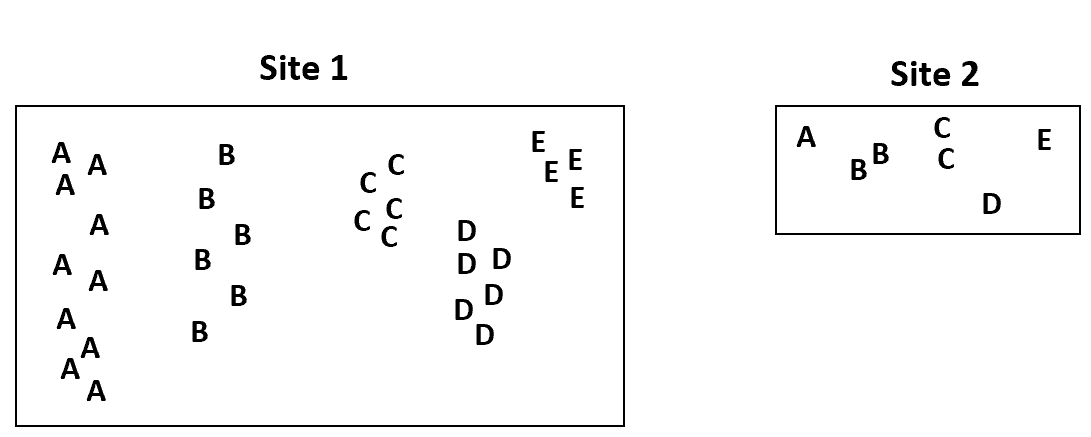
Kami memperkirakan frekuensi spesies yang jauh lebih tinggi di lokasi 1 hanya karena lokasinya jauh lebih besar daripada lokasi 2.

Jadi jika kita menghitung ketidaksamaan Bray-Curtis, hasilnya akan cukup besar. Namun hal ini dapat menyesatkan karena perbedaan antara kedua situs tersebut bukan terletak pada komposisinya, melainkan pada ukurannya.