Cara menghitung ketidaksamaan bray-curtis di r

Ketidaksamaan Bray-Curtis merupakan suatu cara untuk mengukur ketidaksamaan antara dua situs yang berbeda.

Hal ini sering digunakan dalam ekologi dan biologi untuk mengukur perbedaan antara dua lokasi dalam kaitannya dengan spesies yang ditemukan di lokasi tersebut.

Ini dihitung sebagai berikut:

BC _ij = 1 – (2*C _ij ) / (S _i + S _j )

Emas:

• C _ij : Jumlah nilai terendah untuk spesies yang ditemukan pada setiap lokasi.
• S _i : Jumlah seluruh benda uji yang dihitung di lokasi i
• S _j : Jumlah seluruh benda uji yang dihitung di lokasi j

Ketidaksamaan Bray-Curtis selalu antara 0 dan 1 dimana:

• 0 menunjukkan bahwa dua situs tidak memiliki perbedaan. Dengan kata lain, mereka mempunyai jumlah yang sama persis untuk setiap jenis spesies.
• 1 menunjukkan bahwa dua situs memiliki ketidaksamaan total. Dengan kata lain, mereka tidak berbagi spesies apa pun dengan tipe yang sama.

Misalnya, seorang ahli botani keluar dan menghitung jumlah lima spesies tanaman berbeda (A, B, C, D, dan E) di dua lokasi berbeda.

Tabel berikut merangkum data yang dia kumpulkan:

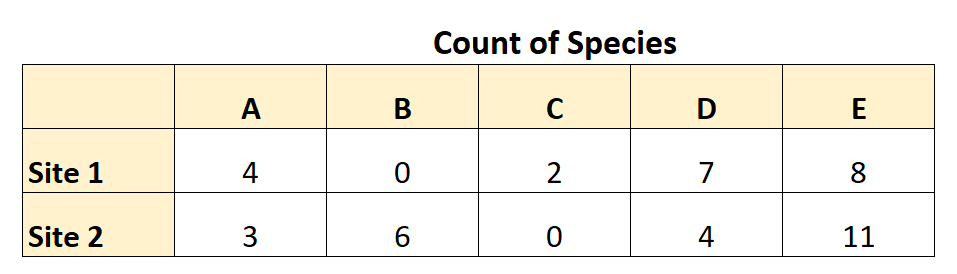
Dengan menggunakan data ini, dia dapat menghitung ketidaksamaan Bray-Curtis sebagai berikut:

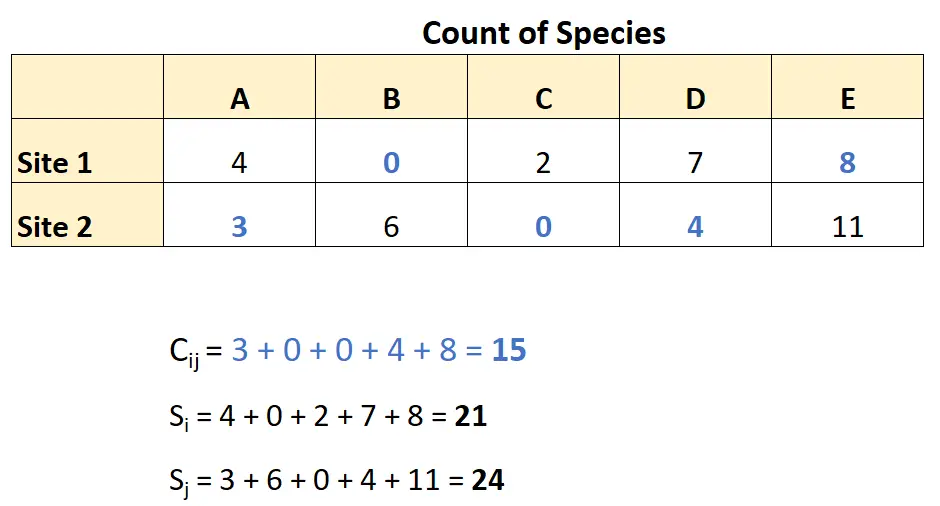
Dengan mengintegrasikan angka-angka ini ke dalam rumus ketidaksamaan Bray-Curtis, kita memperoleh:

• BC _ij = 1 – (2*C _ij ) / (S _i + S _j )
• BC _ij = 1 – (2*15) / (21 + 24)
• SM _ij = 0,33

Ketidaksamaan Bray-Curtis antara kedua situs ini adalah 0,33 .

Contoh berikut menunjukkan cara menghitung ketidaksamaan Bray-Curtis di R.

Contoh: menghitung ketidaksamaan Bray-Curtis di R

Pertama, mari buat bingkai data berikut di R untuk menampung nilai data kita:

 #create data frame
df <- data. frame (A=c(4, 3),
                 B=c(0, 6),
                 C=c(2, 0),
                 D=c(7, 4),
                 E=c(8, 11))

#view data frame
df

  A B C D E
1 4 0 2 7 8
2 3 6 0 4 11

Kita dapat menggunakan kode berikut untuk menghitung ketidaksamaan Bray-Curtis antara dua baris dalam bingkai data:

 #calculate Bray–Curtis dissimilarity
sum( apply (df, 2, function (x) abs ( max (x)- min (x)))) / sum ( rowSums (df))

[1] 0.3333333

Bray-Curtis ternyata berbeda 0,33 .

Ini cocok dengan nilai yang kami hitung secara manual sebelumnya.

Catatan : Rumus ini hanya akan berfungsi jika setiap baris dalam bingkai data mewakili situs terpisah.

Sumber daya tambahan

Tutorial berikut menjelaskan cara menghitung metrik kesamaan lainnya di R:

Cara menghitung kesamaan Jaccard di R
Cara menghitung kesamaan kosinus di R