Koefisien determinasi (r kuadrat)

Oleh Benjamin anderson Agustus 2, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu koefisien determinasi (atau R square) dalam statistik. Jadi, Anda akan mengetahui cara menghitung koefisien determinasi, cara menafsirkannya, dan selain itu, kalkulator online untuk menghitung koefisien determinasi suatu sampel data.

Berapakah koefisien determinasi (R kuadrat)?

Koefisien determinasi yang dilambangkan dengan R ² ( R kuadrat ) merupakan statistik yang mengukur goodness of fit suatu model regresi. Koefisien determinasi menunjukkan seberapa cocok suatu model regresi dengan kumpulan data, yaitu menunjukkan persentase yang dijelaskan oleh model regresi.

Oleh karena itu, semakin tinggi koefisien determinasi maka semakin baik model regresinya. Meskipun kondisi ini tidak selalu terpenuhi, pada prinsipnya kami tertarik pada koefisien determinasi sebesar mungkin. Di bawah ini kita akan melihat bagaimana menafsirkan koefisien determinasi.

Rumus koefisien penentu

Koefisien determinasi sama dengan satu dikurangi perbandingan antara varians sisa dan varians variabel terikat. Koefisien determinasi juga dapat dihitung dengan mengurangkan sisa jumlah kuadrat dengan mengurangkan satu dikurangi jumlah kuadrat.

Jadi rumus menghitung koefisien determinasi adalah sebagai berikut:

rumus koefisien determinasi, rumus r kuadrat

Emas:

$R^2$

adalah koefisien determinasi.
$\sigma_r^2$

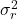
adalah varian sisa.
$\sigma^2$

adalah varians dari variabel terikat Y.
$y_{i}$

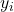
adalah nilai variabel terikat pengamatan i.
$\widehat{y}_{i}$

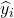
adalah nilai yang didekati dengan model regresi untuk observasi i.
$\overline{y}$

adalah rata-rata variabel terikat di semua pengamatan.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung koefisien determinasi kumpulan data apa pun.

Untuk kasus model regresi linier, koefisien determinasi setara dengan kuadrat koefisien korelasi :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

Emas

$\sigma_{XY}^2$

adalah kovarians variabel X dan Y,

$\sigma_X^2$

Dan

$\sigma_Y^2$

adalah varians masing-masing variabel bebas X dan variabel terikat Y.

Kalkulator Koefisien determinasi

Masukkan contoh data ke dalam kalkulator di bawah ini agar sesuai dengan model regresi linier sederhana dan hitung koefisien determinasinya. Anda perlu memisahkan pasangan datanya, sehingga pada kotak pertama hanya terdapat nilai variabel bebas X dan pada kotak kedua hanya terdapat nilai variabel terikat Y.

Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Interpretasi koefisien determinasi

Pada bagian ini kita akan melihat bagaimana cara mengartikan koefisien determinasi, karena tidak ada gunanya mengetahui nilai koefisien determinasi jika nantinya tidak mengetahui maksudnya.

Nilai koefisien determinasi bisa berkisar antara 0 sampai 1, namun biasanya dinyatakan dalam persentase, sehingga minimumnya adalah 0% dan maksimumnya adalah 100%.

Mengenai interpretasi koefisien determinasi , semakin tinggi nilainya berarti model regresi menjelaskan data sampel dengan lebih baik. Jadi, semakin dekat koefisien determinasi ke 1, maka model tersebut akan semakin disesuaikan. Sebaliknya, semakin mendekati angka 0 maka model regresi yang dihasilkan akan semakin tidak dapat diandalkan.

Namun ketika membandingkan dua model regresi, model dengan koefisien regresi yang lebih tinggi tidak selalu lebih baik. Misalnya, suatu model regresi mungkin memiliki koefisien regresi R ² = 100% karena banyak variabel penjelas yang ditambahkan ke dalam model sehingga dapat menjelaskan semua observasi dengan sempurna. Namun model ini tentunya memberikan prediksi yang sangat buruk untuk nilai baru yang tidak digunakan untuk membangun model regresi.

Perlu diingat juga bahwa model regresi yang dihasilkan memenuhi asumsi sebelumnya. Dengan demikian, model dengan koefisien determinasi yang sangat tinggi tidak ada gunanya jika variabilitas residunya tidak konstan (homoskedastisitas).

Lebih jauh lagi, koefisien determinasi memberikan batasan yang penting karena tidak membatasi pemasukan variabel penjelas. Logikanya, semakin banyak variabel penjelas yang dimiliki suatu model regresi, semakin kompleks pula model tersebut, namun semakin baik model tersebut menjelaskan data yang diamati, sehingga semakin tinggi koefisien determinasinya. Namun, koefisien determinasi yang disesuaikan memperhitungkan jumlah variabel dalam model (kita akan melihat cara penghitungannya di bawah).

Kesimpulannya, koefisien determinasi sangat berguna untuk menganalisis model regresi karena memungkinkan kita mengetahui seberapa cocok model regresi tersebut dengan kumpulan data. Namun, alat lain juga harus digunakan untuk meninjau model yang dihasilkan, seperti grafik statistik .

Koefisien determinasi yang disesuaikan

Koefisien determinasi yang disesuaikan , disebut juga koefisien determinasi yang disesuaikan , mengukur kesesuaian model regresi dengan memperhitungkan jumlah variabel penjelas yang dimasukkan dalam model.

Perbedaan antara koefisien determinasi dan koefisien determinasi yang disesuaikan adalah koefisien determinasi mengukur kualitas penyesuaian tanpa memperhitungkan banyaknya variabel, sebaliknya koefisien determinasi yang disesuaikan mengukur kualitas penyesuaian. memberikan penalti untuk setiap variabel yang ditambahkan.

Rumus untuk menghitung koefisien determinasi yang disesuaikan adalah sebagai berikut:

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

Emas:

$\bar{R}^2$

adalah koefisien determinasi yang disesuaikan.
$R^2$

adalah koefisien determinasi.
$N$

adalah ukuran sampel.
$k$

adalah jumlah variabel penjelas dalam model regresi.

Oleh karena itu, koefisien determinasi yang disesuaikan lebih baik daripada koefisien determinasi untuk membandingkan dua model yang berbeda, karena model tersebut mungkin mempunyai jumlah variabel penjelas yang berbeda.

➤ Lihat: Koefisien determinasi yang disesuaikan

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya