Koefisien korelasi intrakelas: definisi + contoh

Koefisien korelasi intrakelas (ICC) digunakan untuk mengukur reliabilitas skor dalam studi di mana terdapat dua atau lebih penilai.

Nilai ICC dapat berkisar dari 0 hingga 1, dengan 0 menunjukkan tidak ada keandalan di antara penilai dan 1 menunjukkan keandalan sempurna di antara penilai.

Sederhananya, ICC digunakan untuk menentukan apakah item (atau topik) dapat dinilai secara andal oleh penilai yang berbeda.

Ada beberapa versi berbeda dari ICC yang dapat dihitung, bergantung pada tiga faktor berikut:

• Model: efek acak satu arah, efek acak dua arah, atau efek campuran dua arah
• Jenis hubungan: konsistensi atau kesepakatan mutlak
• Unit: penilai tunggal atau rata-rata penilai

Berikut penjelasan singkat ketiga model berbeda tersebut:

1. Model efek acak satu arah: Model ini mengasumsikan bahwa setiap mata pelajaran dievaluasi oleh kelompok penilai berbeda yang dipilih secara acak. Dengan model ini, penilai dianggap sebagai sumber efek acak. Model ini jarang digunakan dalam praktik karena kelompok penilai yang sama umumnya digunakan untuk menilai setiap mata pelajaran.

2. Model efek acak dua arah: Model ini mengasumsikan bahwa sekelompok penilai k dipilih secara acak dari suatu populasi dan kemudian digunakan untuk menilai subjek. Dengan menggunakan model ini, penilai dan subjek dianggap sebagai sumber efek acak. Model ini sering digunakan ketika kita ingin menggeneralisasi hasil kita kepada penilai yang serupa dengan yang digunakan dalam penelitian.

3. Model efek campuran dua arah: Model ini juga mengasumsikan bahwa sekelompok penilai k dipilih secara acak dari suatu populasi dan kemudian digunakan untuk menilai subjek. Namun, model ini mengasumsikan bahwa kelompok penilai yang kami pilih adalah satu-satunya penilai yang berkepentingan, artinya kami tidak ingin menggeneralisasikan hasil kami kepada penilai lain yang mungkin juga memiliki karakteristik serupa dengan penilai yang digunakan dalam penelitian ini.

Berikut ini penjelasan singkat tentang dua jenis hubungan berbeda yang mungkin ingin kita ukur:

1. Konsistensi: Kami tertarik pada perbedaan sistematis antara penilaian para juri (misalnya, apakah para juri menilai topik serupa sebagai rendah dan tinggi?)

2. Kesepakatan mutlak: kami tertarik pada perbedaan mutlak antara nilai para juri (misalnya, berapakah perbedaan mutlak antara nilai hakim A dan hakim B?)

Berikut adalah penjelasan singkat tentang dua unit berbeda yang mungkin menarik bagi kami:

1. Peninjau tunggal: Kami hanya ingin menggunakan penilaian satu pengulas sebagai dasar pengukuran.

2. Rata-rata penilai: Kami ingin menggunakan rata-rata skor seluruh juri sebagai dasar pengukuran.

Catatan: Jika Anda ingin mengukur tingkat kesepakatan antara dua penilai yang melewatkan setiap item pada hasil dikotomis , Anda sebaiknya menggunakan Kappa Cohen .

Bagaimana menafsirkan koefisien korelasi intrakelas

Berikut cara mengartikan nilai koefisien korelasi intrakelas menurut Koo & Li :

• Kurang dari 0,50: keandalan buruk
• Antara 0,5 dan 0,75: Keandalan sedang
• Antara 0,75 dan 0,9: Keandalan yang baik
• Lebih besar dari 0,9: Keandalan luar biasa

Contoh berikut menunjukkan cara menghitung koefisien korelasi intrakelas dalam praktiknya.

Contoh: Perhitungan koefisien korelasi intrakelas

Misalkan empat juri berbeda diminta untuk mengevaluasi kualitas 10 ujian masuk perguruan tinggi yang berbeda. Hasilnya ditunjukkan di bawah ini:

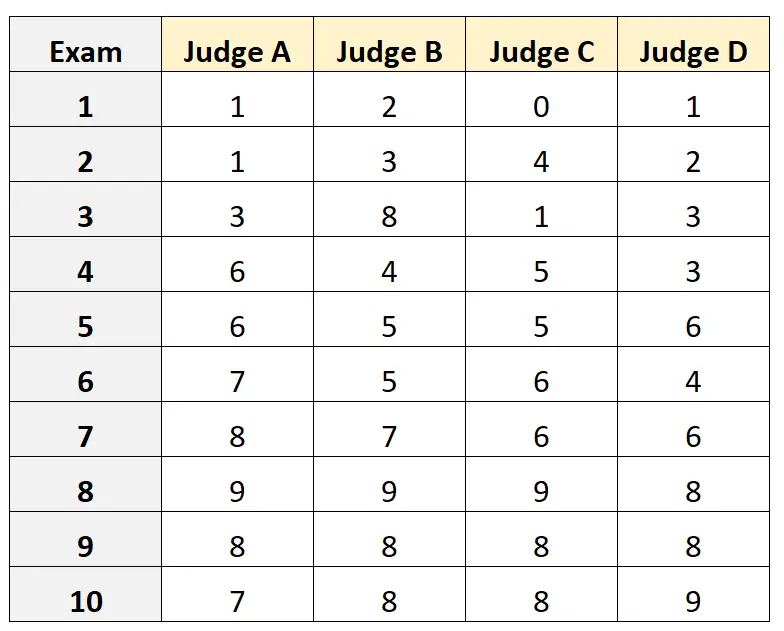
Misalkan keempat juri dipilih secara acak dari populasi juri yang memenuhi syarat untuk ujian masuk dan kita ingin mengukur kesepakatan mutlak antara juri dan kita ingin menggunakan skor dari sudut pandang satu evaluator saja sebagai dasar pengukuran kita.

Kita dapat menggunakan kode berikut di R agar sesuai dengan model efek acak dua arah , menggunakan kesepakatan absolut sebagai hubungan antara penilai dan menggunakan unit tunggal sebagai unit kepentingan:

 #load the interrater reliability package
library (irr)

#define data
data <- data. frame (A=c(1, 1, 3, 6, 6, 7, 8, 9, 8, 7),
                   B=c(2, 3, 8, 4, 5, 5, 7, 9, 8, 8),
                   C=c(0, 4, 1, 5, 5, 6, 6, 9, 8, 8),
                   D=c(1, 2, 3, 3, 6, 4, 6, 8, 8, 9))

#calculate ICC
icc(data, model = " twoway ", type = " agreement ", unit = " single ")

   Model: twoway 
   Type: agreement 

   Subjects = 10 
     Failures = 4 
   ICC(A,1) = 0.782

 F-Test, H0: r0 = 0; H1: r0 > 0 
    F(9.30) = 15.3, p = 5.93e-09 

 95%-Confidence Interval for ICC Population Values:
  0.554 < ICC < 0.931

Koefisien korelasi intrakelas (ICC) ditemukan sebesar 0,782 .

Berdasarkan aturan praktis dalam menafsirkan ICC, kami dapat menyimpulkan bahwa ICC sebesar 0,782 menunjukkan bahwa ujian dapat dinilai dengan reliabilitas “baik” oleh penilai yang berbeda.

Sumber daya tambahan

Tutorial berikut memberikan penjelasan rinci tentang cara menghitung ICC di berbagai software statistik:

Cara Menghitung Koefisien Korelasi Intrakelas di Excel
Cara menghitung koefisien korelasi intrakelas di R
Cara Menghitung Koefisien Korelasi Intrakelas dengan Python