Cara menghitung koefisien korelasi pada kalkulator ti-84
Koefisien korelasi adalah ukuran hubungan linier antara dua variabel. Ini dapat mengambil nilai antara -1 dan 1 di mana:
- -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
- 0 menunjukkan tidak ada korelasi linier antara dua variabel
- Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel
Anda dapat menggunakan langkah-langkah berikut untuk menghitung koefisien korelasi antara dua variabel pada kalkulator TI-84:
Langkah 1: Aktifkan diagnostik.
Pertama, kita perlu mengaktifkan diagnostik. Caranya, tekan 2 lalu tekan angka 0. Ini akan membawa kita ke layar KATALOG.
Gulir ke DiagnosticOn dan tekan ENTER .
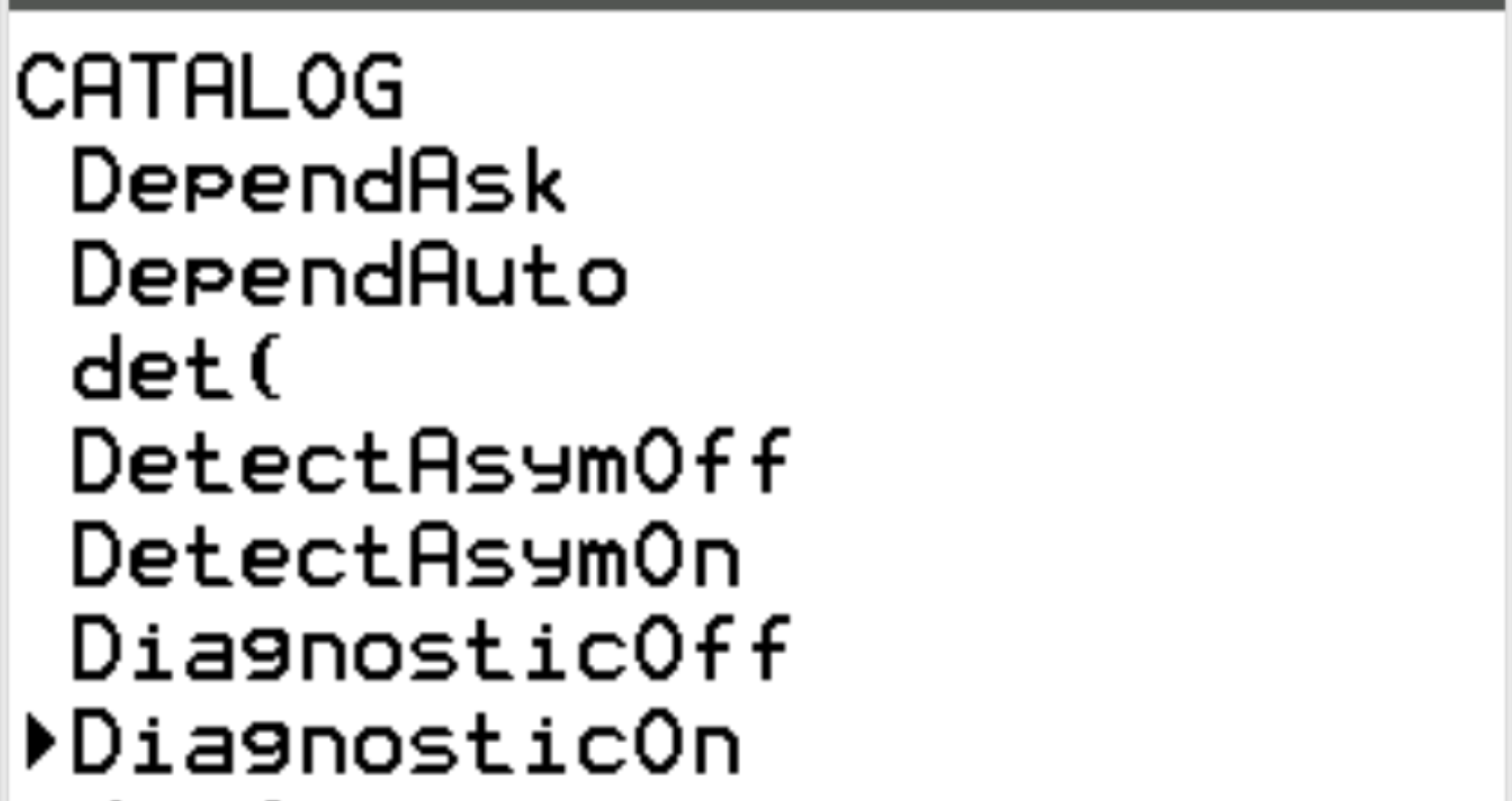
Kemudian tekan ENTER lagi.
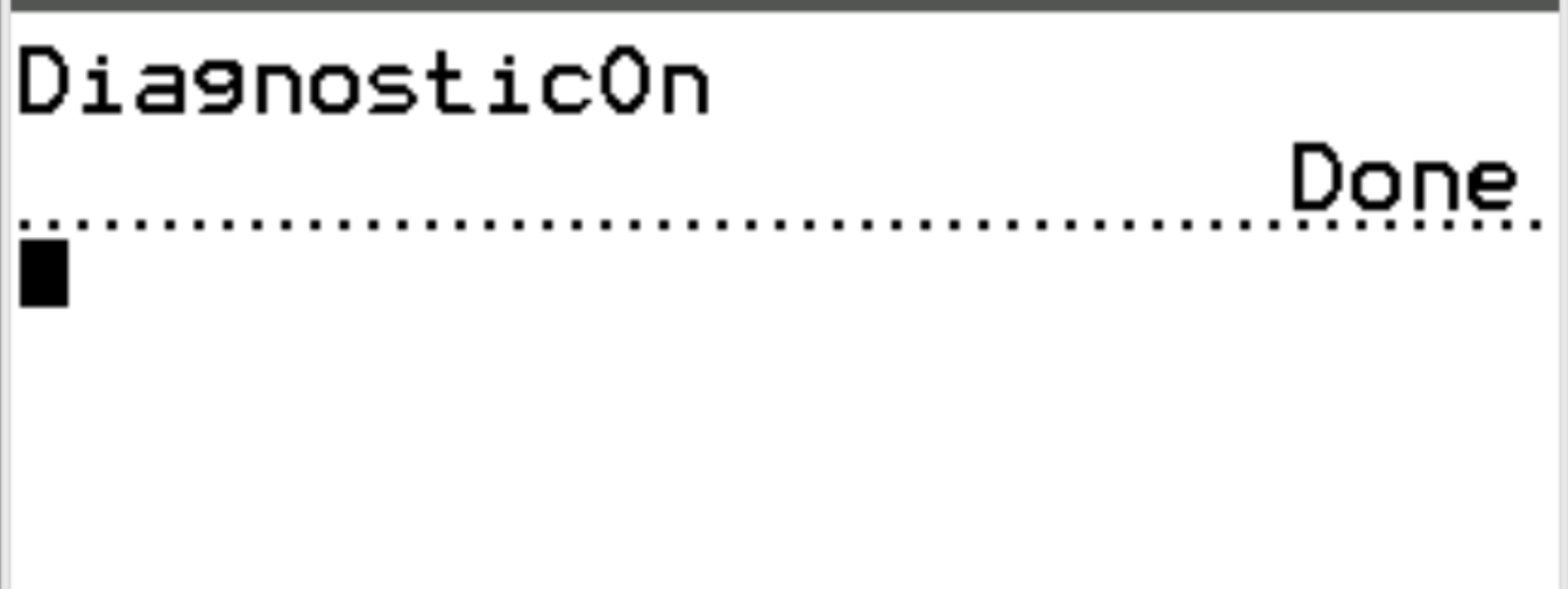
Diagnostik kini diaktifkan sehingga kami dapat menghitung koefisien korelasi antara dua variabel.
Langkah 2: Masukkan datanya.
Selanjutnya, kita perlu memasukkan nilai data untuk kedua variabel kita. Tekan Stat lalu tekan EDIT . Masukkan nilai variabel pertama pada kolom L1 dan nilai variabel kedua pada kolom L2:
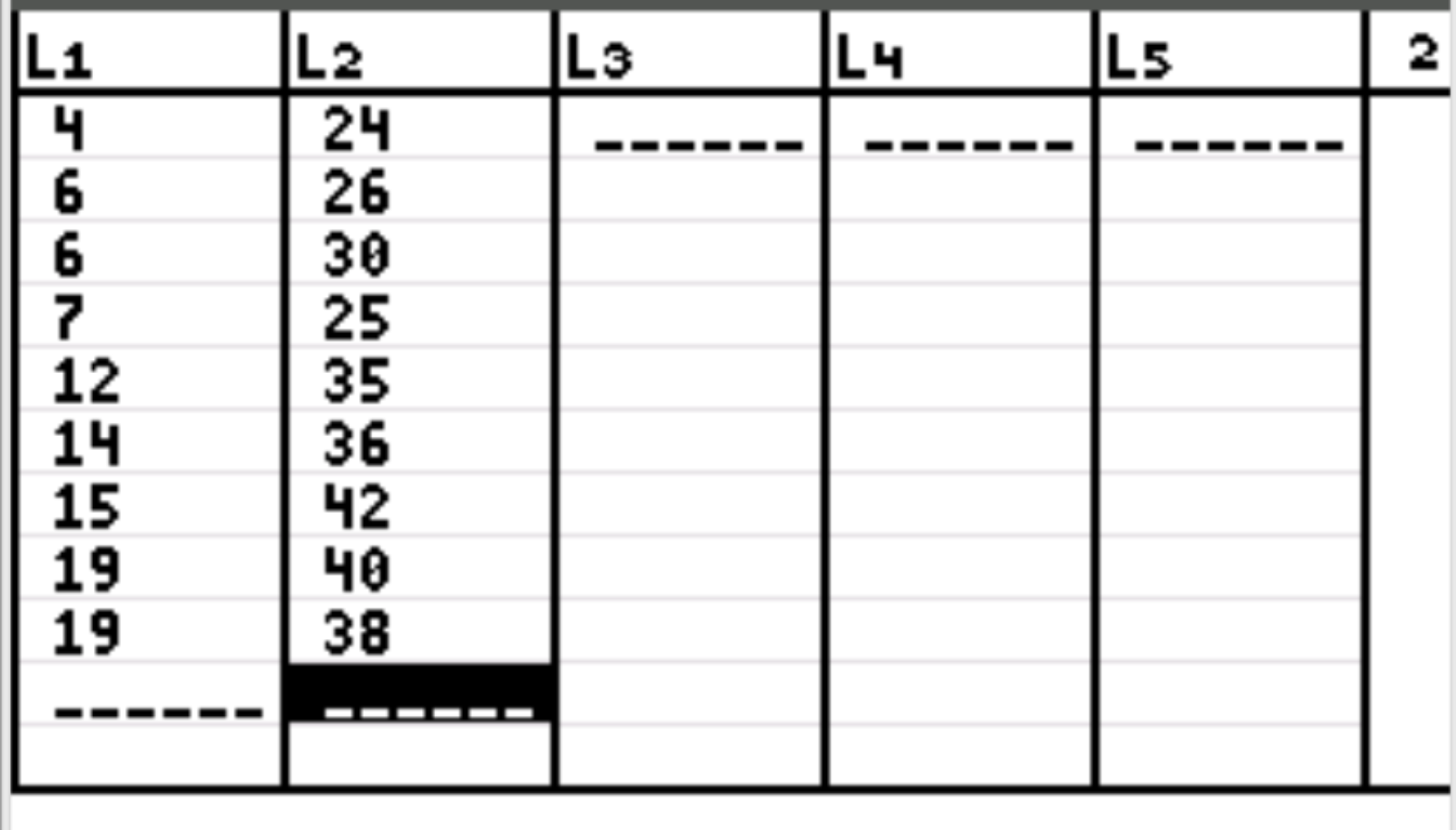
Langkah 3: Temukan koefisien korelasi.
Selanjutnya kita akan menghitung koefisien korelasi kedua variabel tersebut. Tekan Stat lalu gulir ke CALC . Kemudian gulir ke 8: Linreg(a+bx) dan tekan Enter .
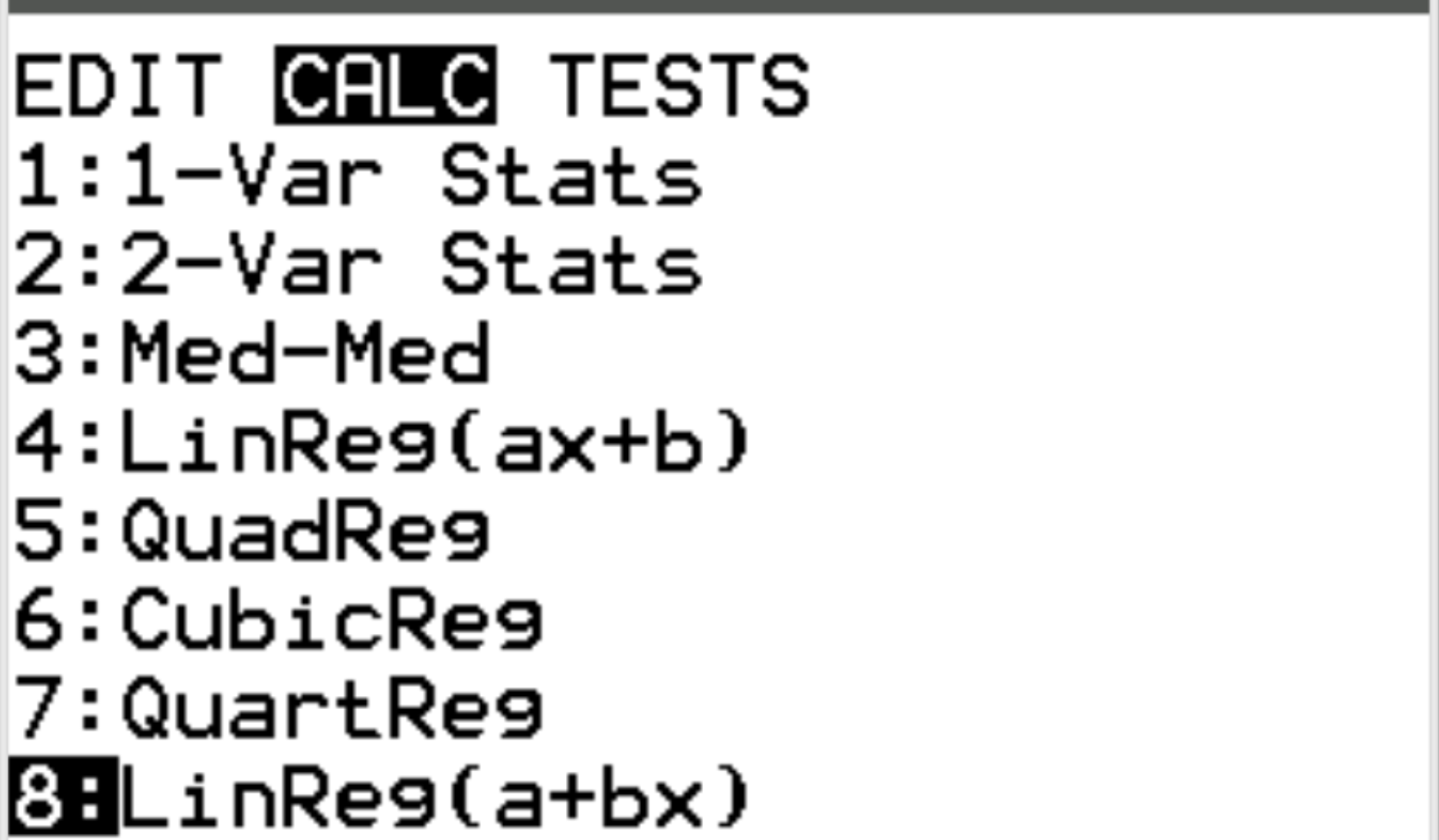
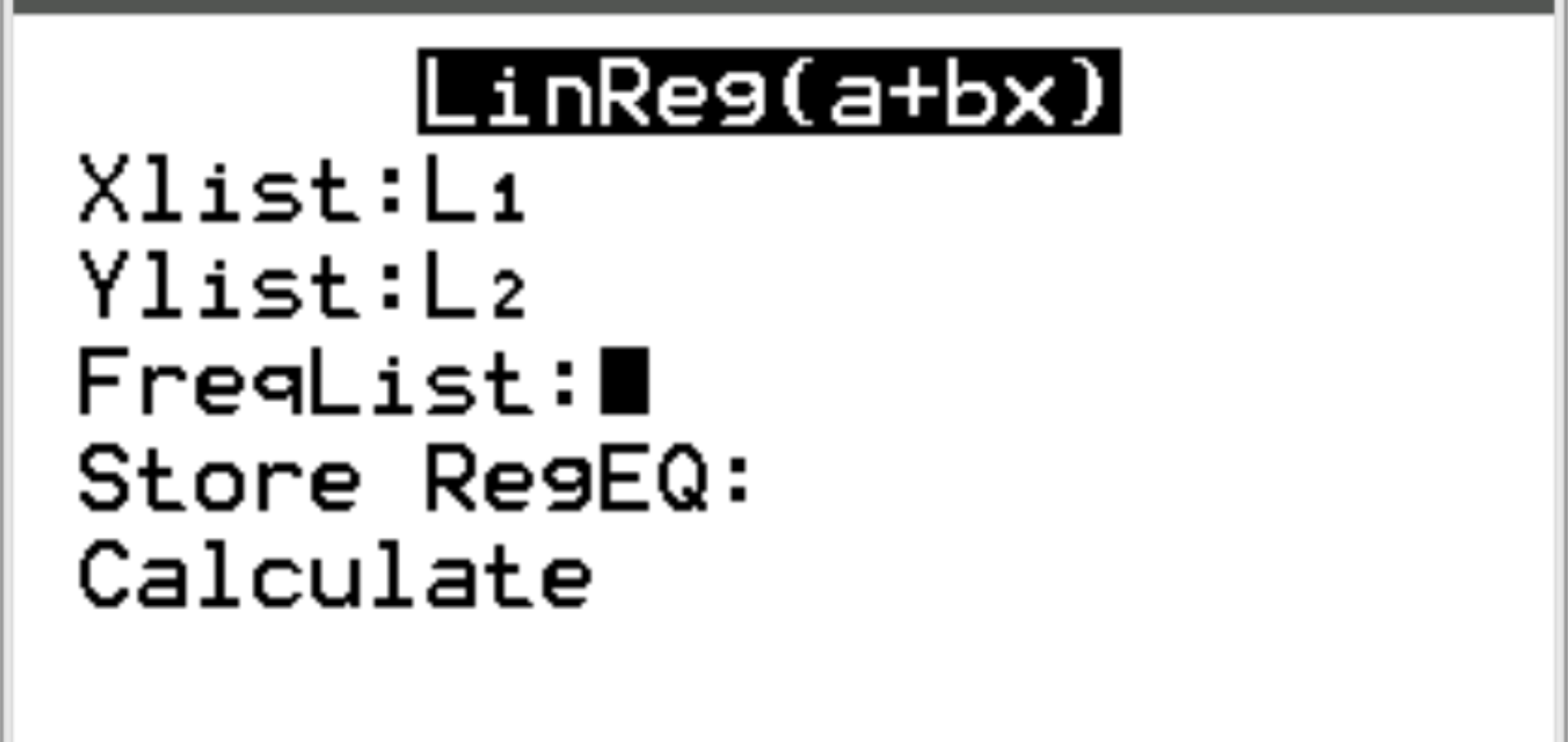
Untuk Xlist dan Ylist pastikan L1 dan L2 dipilih karena ini adalah kolom yang kita gunakan untuk memasukkan data kita. Biarkan FreqList kosong. Gulir ke bawah ke Hitung dan tekan Enter .
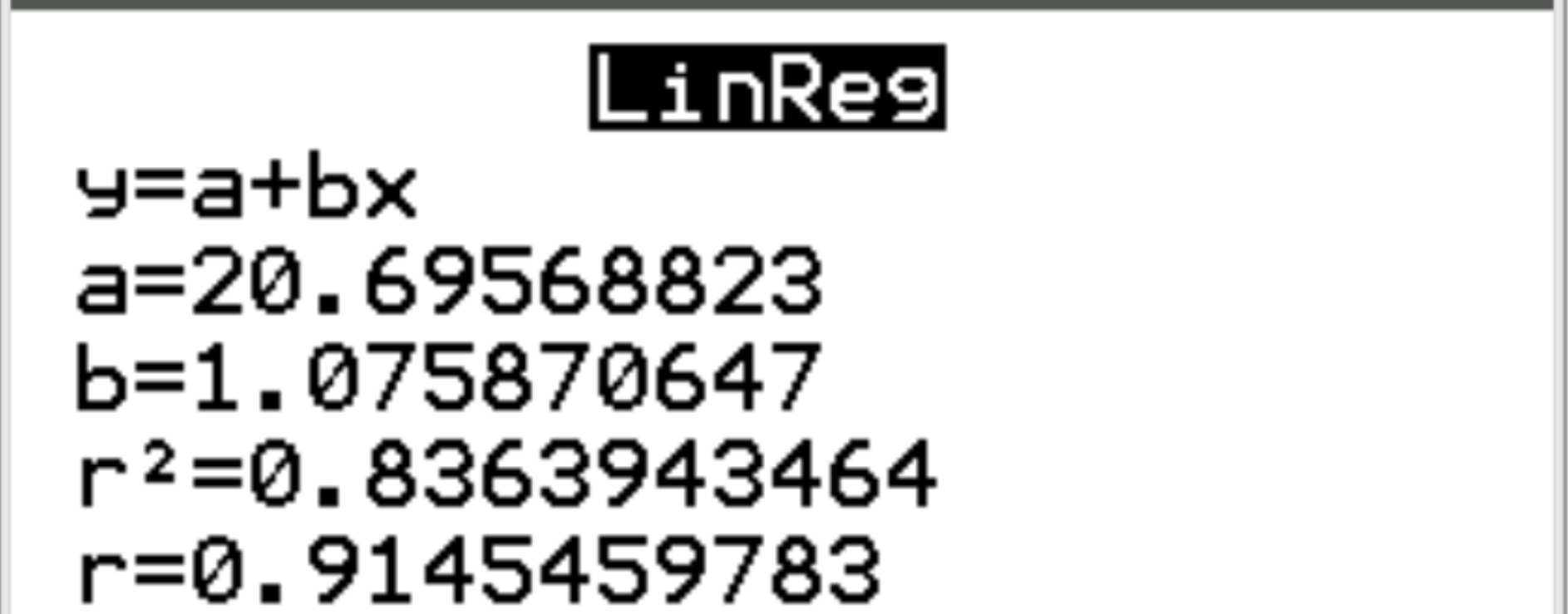
Pada layar baru kita dapat melihat bahwa koefisien korelasi (r) antara kedua variabel adalah 0,9145 .
Bagaimana menafsirkan koefisien korelasi
Tabel berikut menunjukkan aturan praktis untuk menafsirkan kekuatan hubungan dua variabel berdasarkan nilai r :
| Nilai mutlak r | Kekuatan hubungan |
|---|---|
| r <0,25 | Tidak ada hubungan |
| 0,25 < r < 0,5 | Hubungan yang lemah |
| 0,5 < r < 0,75 | Hubungan yang moderat |
| r > 0,75 | Hubungan yang kuat |
Dalam contoh kita, koefisien korelasi sebesar 0,9145 menunjukkan hubungan positif yang kuat antara kedua variabel.
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya