Koefisien korelasi pearson

Koefisien korelasi Pearson (juga dikenal sebagai “koefisien korelasi momen produk”) adalah ukuran hubungan linier antara dua variabel X dan Y. Nilainya antara -1 dan 1 dengan:

• -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
• 0 menunjukkan tidak ada korelasi linier antara dua variabel
• Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel

Rumus mencari koefisien korelasi Pearson

Rumus mencari koefisien korelasi Pearson yang dilambangkan r untuk sampel data adalah ( melalui Wikipedia ):

Anda mungkin tidak perlu menghitung rumus ini secara manual karena Anda dapat menggunakan perangkat lunak untuk melakukannya, namun akan sangat membantu jika Anda memahami fungsi sebenarnya rumus ini dengan melihat contohnya.

Misalkan kita memiliki kumpulan data berikut:

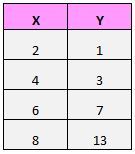
Jika kita memplot pasangan ini (X, Y) pada plot sebar, maka akan terlihat seperti ini:

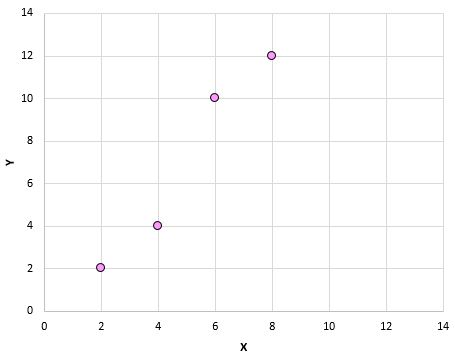
Hanya dengan melihat scatterplot ini, kita dapat melihat bahwa terdapat hubungan positif antara variabel X dan Y: seiring dengan bertambahnya X, maka Y juga cenderung meningkat. Namun untuk mengukur dengan tepat seberapa positif kedua variabel ini berhubungan, kita perlu mencari koefisien korelasi Pearson.

Mari kita fokus saja pada pembilang rumusnya:

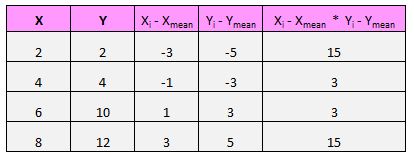
Untuk setiap pasangan (X, Y) dalam kumpulan data kita, kita perlu mencari selisih antara nilai x dan nilai rata-rata x, selisih antara nilai y dan nilai rata-rata y, lalu mengalikan kedua angka tersebut.

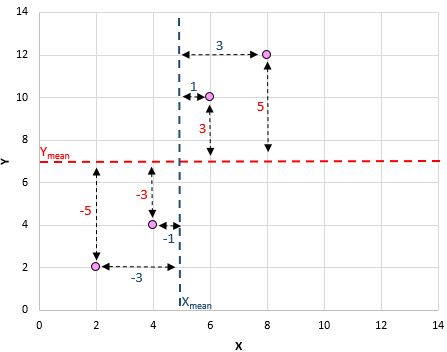
Misalnya pasangan pertama kita (X, Y) adalah (2, 2). Nilai rata-rata x pada kumpulan data ini adalah 5 dan nilai rata-rata y pada kumpulan data ini adalah 7. Jadi selisih antara nilai x pasangan ini dengan nilai rata-rata x adalah 2 – 5 = -3. Selisih antara nilai y pasangan ini dengan nilai rata-rata y adalah 2 – 7 = -5. Lalu jika kita mengalikan kedua bilangan tersebut kita mendapatkan -3 * -5 = 15.

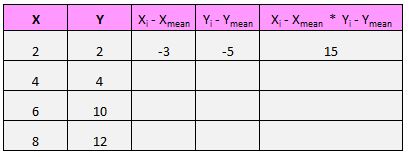
Berikut gambaran visual tentang apa yang baru saja kami lakukan:

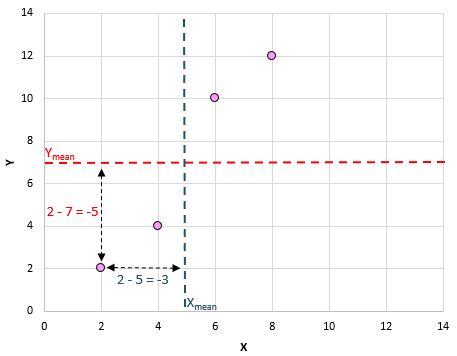
Kemudian lakukan saja ini untuk setiap pasangan:

Langkah terakhir untuk mendapatkan pembilang rumusnya adalah dengan menjumlahkan semua nilai ini:

15 + 3 +3 + 15 = 36

Kemudian penyebut rumusnya menyuruh kita mencari jumlah semua selisih kuadrat untuk x dan y, lalu kalikan kedua angka tersebut, lalu ambil akar kuadratnya:

Pertama kita cari jumlah kuadrat selisih x dan y:

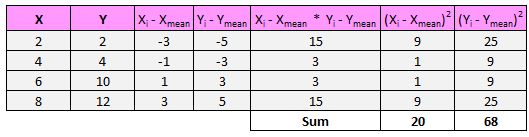
Selanjutnya, kita kalikan kedua angka ini: 20 * 68 = 1,360.

Terakhir, kita ambil akar kuadratnya: √ 1,360 = 36,88

Jadi kita menemukan bahwa pembilang rumusnya adalah 36 dan penyebutnya adalah 36,88. Artinya koefisien korelasi Pearson kita adalah r = 36 / 36,88 = 0,976

Angka ini mendekati 1, menunjukkan bahwa terdapat hubungan linier positif yang kuat antara variabel X dan Y. Hal ini menegaskan hubungan yang kami amati dalam diagram sebar.

Lihat korelasi

Ingatlah bahwa koefisien korelasi Pearson menunjukkan jenis hubungan linier (positif, negatif, tidak ada) antara dua variabel serta kekuatan hubungan tersebut (lemah, sedang, kuat).

Saat kita membuat scatterplot dua variabel, kita dapat melihat hubungan nyata antara dua variabel. Berikut adalah berbagai jenis hubungan linier yang mungkin kita amati:

Hubungan yang kuat dan positif: Semakin besar variabel pada sumbu x, maka variabel pada sumbu y juga meningkat. Poin-poin tersebut berkerumun erat, menunjukkan hubungan yang kuat.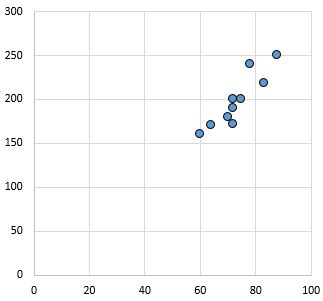

Koefisien korelasi Pearson: 0,94

Hubungan lemah dan positif: Semakin besar variabel pada sumbu x, maka variabel pada sumbu y juga meningkat. Titik-titiknya cukup tersebar, menunjukkan hubungan yang lemah.

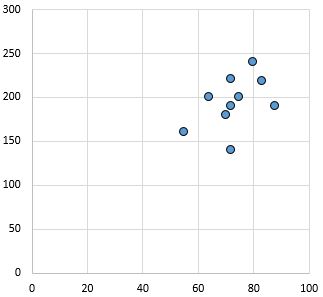
Koefisien korelasi Pearson: 0,44

Tidak ada hubungan: Tidak ada hubungan yang jelas (positif atau negatif) antar variabel.

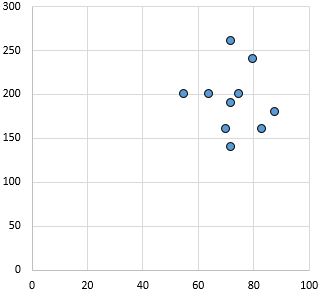
Koefisien korelasi Pearson: 0,03

Hubungan kuat dan negatif: Semakin besar variabel pada sumbu x, maka variabel pada sumbu y berkurang. Poin-poinnya tersusun rapat, menunjukkan hubungan yang kuat.

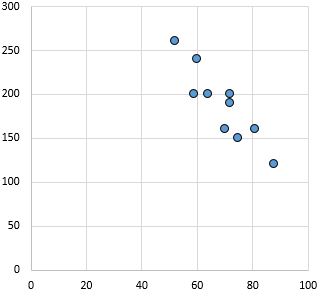
Koefisien korelasi Pearson: -0,87

Hubungan lemah dan negatif: Semakin besar variabel pada sumbu x, maka variabel pada sumbu y berkurang. Titik-titiknya cukup tersebar, menunjukkan hubungan yang lemah.

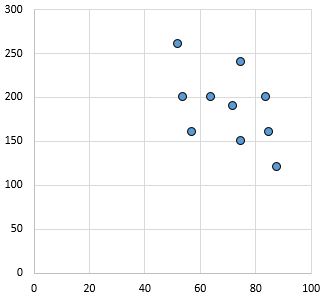
Koefisien korelasi Pearson: – 0,46

Menguji signifikansi koefisien korelasi Pearson

Saat kita menemukan koefisien korelasi Pearson untuk sekumpulan data, kita sering kali menggunakan sampel data dari populasi yang lebih besar. Artinya, korelasi bukan nol dapat ditemukan untuk dua variabel meskipun kedua variabel tersebut sebenarnya tidak berkorelasi dalam populasi secara keseluruhan.

Misalnya, kita membuat plot sebar untuk variabel X dan Y untuk setiap titik data di seluruh populasi dan tampilannya seperti ini:

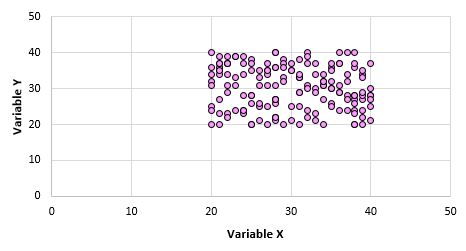
Jelas bahwa kedua variabel ini tidak berkorelasi. Namun, ada kemungkinan ketika kita mengambil sampel 10 titik dari populasi, kita memilih titik-titik berikut:

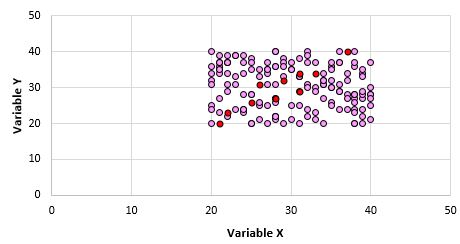
Kita dapat melihat bahwa koefisien korelasi Pearson untuk titik sampel ini adalah 0,93, menunjukkan korelasi positif yang kuat meskipun korelasi populasinya nol.

Untuk menguji apakah suatu korelasi antara dua variabel signifikan atau tidak secara statistik, kita dapat menemukan statistik uji berikut:

Statistik uji T = r * √ (n-2) / (1-r ² )

di mana n adalah jumlah pasangan dalam sampel kita, r adalah koefisien korelasi Pearson, dan statistik uji T mengikuti distribusi dengan n-2 derajat kebebasan.

Mari kita tinjau contoh cara menguji signifikansi koefisien korelasi Pearson.

Contoh

Kumpulan data berikut menunjukkan tinggi dan berat badan 12 orang:

Plot sebar di bawah ini menunjukkan nilai kedua variabel tersebut:

Koefisien korelasi Pearson kedua variabel tersebut adalah r = 0,836.

Statistik uji T = 0,836 * √ (12 -2) / (1-0,836 ² ) = 4,804.

Menurut kalkulator distribusi t kami, skor 4,804 dengan 10 derajat kebebasan memiliki nilai p 0,0007. Karena 0,0007 < 0,05, kita dapat menyimpulkan bahwa korelasi antara berat badan dan tinggi badan dalam contoh ini signifikan secara statistik pada alfa = 0,05.

Tindakan pencegahan

Meskipun koefisien korelasi Pearson dapat berguna untuk mengetahui apakah dua variabel mempunyai hubungan linier atau tidak, kita perlu mengingat tiga hal saat menafsirkan koefisien korelasi Pearson:

1. Korelasi tidak berarti sebab akibat. Hal ini bukan karena dua variabel berkorelasi sehingga variabel yang satu menyebabkan variabel yang lain lebih sering atau lebih jarang muncul. Contoh klasiknya adalah korelasi positif antara penjualan es krim dan serangan hiu. Ketika penjualan es krim meningkat pada waktu-waktu tertentu dalam setahun, serangan hiu juga cenderung meningkat.

Apakah ini berarti makan es krim menyebabkan serangan hiu? Tentu saja tidak! Artinya di musim panas, konsumsi es dan serangan hiu cenderung meningkat, karena es lebih populer di musim panas dan lebih banyak orang pergi ke laut selama musim panas.

2. Korelasi sensitif terhadap outlier. Pencilan ekstrim dapat mengubah koefisien korelasi Pearson secara signifikan. Perhatikan contoh di bawah ini:

Variabel X dan Y mempunyai koefisien korelasi Pearson sebesar 0,00 . Tapi bayangkan kita memiliki pencilan dalam kumpulan data:

Namun koefisien korelasi Pearson kedua variabel tersebut sebesar 0,878 . Pencilan yang satu ini mengubah segalanya. Inilah sebabnya, saat menghitung korelasi dua variabel, sebaiknya visualisasikan variabel tersebut menggunakan plot sebar untuk memeriksa outlier.

3. Koefisien korelasi Pearson tidak menggambarkan hubungan nonlinier antara dua variabel. Bayangkan kita mempunyai dua variabel dengan hubungan sebagai berikut:

Koefisien korelasi Pearson kedua variabel tersebut sebesar 0,00 karena tidak mempunyai hubungan linier. Namun, kedua variabel ini memiliki hubungan non-linier: nilai y hanyalah nilai x yang dikuadratkan.

Saat menggunakan koefisien korelasi Pearson, ingatlah bahwa Anda hanya menguji apakah dua variabel berhubungan linier . Sekalipun koefisien korelasi Pearson menunjukkan bahwa dua variabel tidak berkorelasi, keduanya mungkin masih mempunyai hubungan nonlinier. Ini adalah alasan lain mengapa membuat diagram sebar berguna saat menganalisis hubungan antara dua variabel: ini dapat membantu Anda mendeteksi hubungan nonlinier.