Koefisien korelasi pearson

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu koefisien korelasi Pearson (atau koefisien korelasi linier) dan kegunaannya. Anda akan menemukan cara menghitung koefisien korelasi Pearson beserta latihan langkah demi langkah. Selain itu, Anda dapat menemukan nilai Koefisien Korelasi Pearson dari kumpulan data mana pun dengan kalkulator online di bagian akhir.

Berapa koefisien korelasi Pearson?

Koefisien korelasi Pearson , disebut juga koefisien korelasi linier atau sekadar koefisien korelasi , adalah ukuran statistik yang menunjukkan hubungan antara dua variabel.

Untuk menghitung koefisien korelasi Pearson antara dua variabel, Anda harus membagi kovarians variabel tersebut dengan akar kuadrat hasil kali variansnya.

Dengan demikian, koefisien korelasi Pearson berupaya mengukur ketergantungan linier antara dua variabel acak kuantitatif. Secara apriori, mengevaluasi korelasi antar variabel secara numerik adalah rumit karena sulit untuk menentukan pasangan variabel mana yang lebih berkorelasi jika, seperti dalam pues, objek koefisien korelasi Pearson adalah menilai hubungan antar variabel agar dapat bandingkan di antara mereka.

Nilai indeks korelasi Pearson adalah antara -1 dan +1 inklusif. Di bawah ini kita akan melihat bagaimana nilai koefisien korelasi Pearson diinterpretasikan.

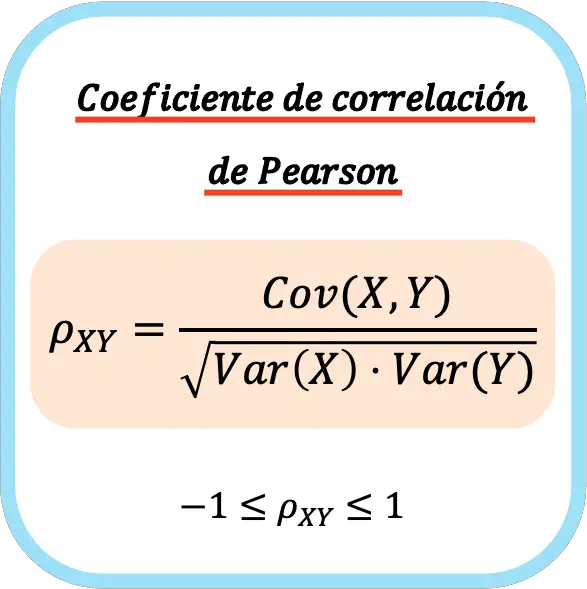
Rumus Koefisien Korelasi Pearson

Koefisien korelasi Pearson dua variabel statistik sama dengan hasil bagi antara kovarians variabel dan akar kuadrat hasil kali varians masing-masing variabel.

Oleh karena itu rumus menghitung koefisien korelasi Pearson adalah sebagai berikut:

Koefisien korelasi Pearson, koefisien korelasi linier

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung koefisien korelasi Pearson untuk kumpulan data apa pun.

Jika koefisien korelasi Pearson dihitung pada suatu populasi, umumnya dinyatakan dengan huruf Yunani ρ. Namun ketika koefisien dihitung relatif terhadap suatu sampel, huruf r biasanya digunakan sebagai simbol.

Perlu diingat bahwa untuk menentukan koefisien korelasi Pearson, Anda harus mengetahui cara menghitung kovarians antara dua variabel dan varians suatu variabel. Selain itu, Anda perlu memahami apa arti pengukuran statistik ini. Oleh karena itu, sebelum melanjutkan penjelasannya, disarankan untuk membaca dua artikel berikut ini:

➤ Lihat: cara menghitung kovarians
➤ Lihat: cara menghitung selisihnya

Contoh penghitungan koefisien korelasi Pearson

Mengingat definisi koefisien korelasi Pearson dan rumusnya, di bawah ini adalah contoh langkah demi langkah sehingga Anda dapat melihat cara menghitungnya.

Hitung koefisien korelasi Pearson antara dua variabel kontinu berikut:

Sebelum menghitung koefisien korelasi Pearson, kami akan merepresentasikan kumpulan data dalam plot sebar untuk menganalisis hubungan antara kedua variabel:

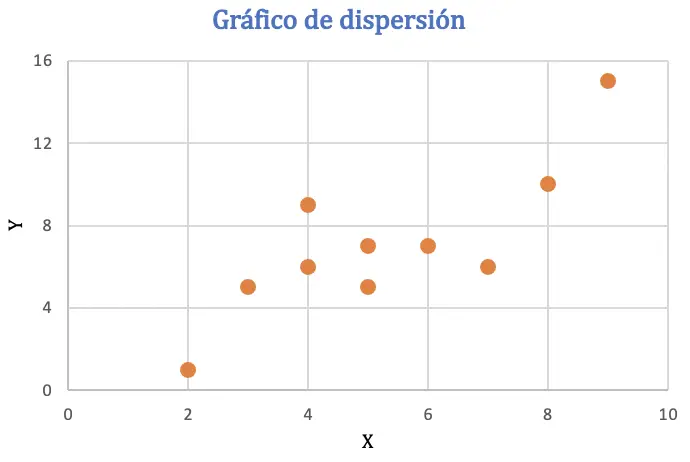
Dari scatter plot tersebut dapat disimpulkan bahwa data tersebut mungkin mempunyai tren yang positif, atau dengan kata lain ketika salah satu variabel meningkat nilainya, maka variabel lainnya juga meningkat. Untuk memeriksa korelasinya, kita akan mencari koefisien Pearson.

Hal pertama yang harus dilakukan adalah mencari mean aritmatika masing-masing variabel secara terpisah, yang setara dengan jumlah total data dibagi dengan jumlah observasi.

$\overline{x}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}=\cfrac{53}{10}=5,3$

$\overline{y}=\cfrac{\displaystyle \sum_{i=1}^n y_i}{n}=\cfrac{71}{10}=7,1$

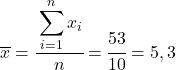
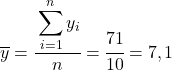
Sekarang kita mengetahui rata-rata setiap variabel, kita perlu menambahkan kolom berikut ke tabel data:

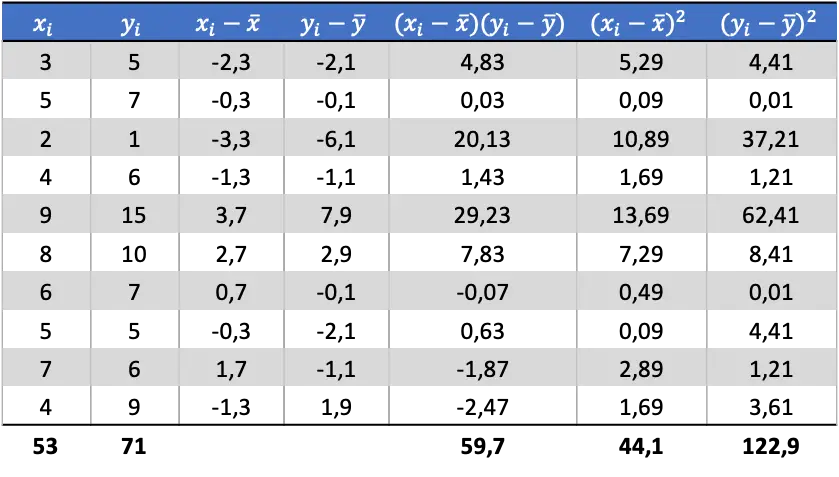
Tabel data perhitungan koefisien Pearson

Dari data perhitungan pada tabel, kami menentukan nilai kovarians dan varians (jika Anda tidak ingat bagaimana hal ini dilakukan, ada dua tautan di atas yang menjelaskannya secara rinci):

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}=\cfrac{59,7}{10}=5,97$

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{x}\right)^2}{n}=\cfrac{44,1}{10}=4,41$

$Var(Y)=\cfrac{\displaystyle\sum_{i=1}^n\left(y_i-\overline{y}\right)^2}{n}=\cfrac{122,9}{10}=12,29$

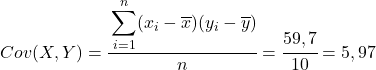
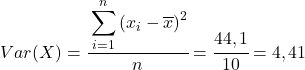
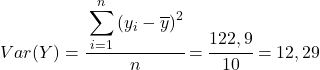
Terakhir, cukup terapkan rumus koefisien korelasi Pearson untuk mendapatkan nilainya:

$\rho_{XY}=\cfrac{Cov(X,Y)}{\sqrt{Var(X)\cdot Var(Y)}}=\cfrac{5,97}{\sqrt{4,41\cdot 12,29}}=0,81$

Koefisien korelasi Pearson mempunyai nilai yang sangat mendekati 1 yang berarti kedua variabel tersebut mempunyai korelasi positif yang cukup kuat.

Seperti yang Anda lihat, untuk menentukan koefisien korelasi Pearson sangat berguna menggunakan program seperti Excel untuk melakukan penghitungan kolom dengan lebih cepat.

Kalkulator Koefisien Korelasi Pearson

Masukkan sekumpulan data statistik ke dalam kalkulator berikut untuk menghitung koefisien korelasi Pearson antara dua variabel. Anda perlu memisahkan pasangan datanya, sehingga pada kotak pertama hanya terdapat nilai satu variabel dan pada kotak kedua hanya terdapat nilai variabel kedua.

Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Menafsirkan Koefisien Korelasi Pearson

Pada bagian ini kita akan melihat bagaimana mengartikan koefisien korelasi Pearson, karena mengetahui nilainya saja tidak cukup, tetapi Anda harus mengetahui bagaimana menganalisis maknanya.

Jadi penafsiran koefisien korelasi Pearson bergantung pada nilainya:

r=-1 : kedua variabel mempunyai korelasi negatif sempurna, sehingga kita dapat menarik garis dengan kemiringan negatif yang menghubungkan semua titik.
-1<r<0 : korelasi kedua variabel bernilai negatif, sehingga jika salah satu variabel meningkat maka variabel lainnya menurun. Semakin dekat nilainya dengan -1, maka variabel-variabel tersebut mempunyai hubungan yang semakin negatif.
r=0 : korelasi kedua variabel sangat lemah, bahkan hubungan linier keduanya adalah nol. Hal ini tidak berarti bahwa variabel-variabel tersebut independen, karena bisa saja mempunyai hubungan non-linier.
0<r<1 : korelasi kedua variabel bernilai positif, semakin mendekati +1 maka semakin kuat hubungan antar variabel. Dalam hal ini, suatu variabel cenderung meningkat nilainya ketika variabel lainnya juga meningkat.
r=1 : kedua variabel mempunyai korelasi positif sempurna, yaitu mempunyai hubungan linier positif.

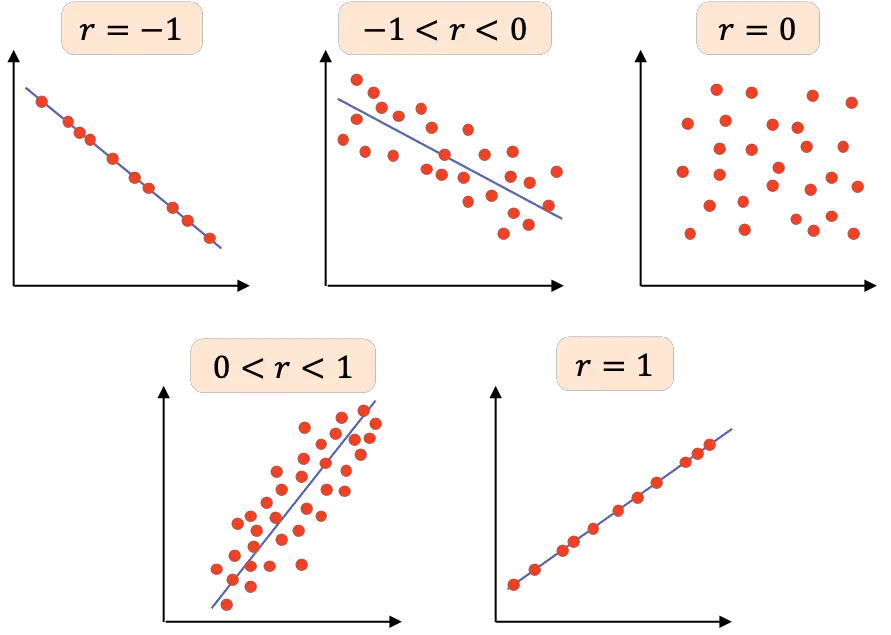
Secara ringkas disajikan tabel berikut dengan perbedaan interpretasi koefisien korelasi Pearson:

Nilai	Penafsiran
r=-1	Korelasi negatif sempurna.
-1<r<0	Korelasi negatif: semakin dekat korelasinya dengan -1, maka semakin kuat korelasinya.
r=0	Korelasi linier nol.
0<r<1	Korelasi positif: semakin dekat korelasinya dengan +1, semakin kuat korelasinya.
r=1	Korelasi positif sempurna.

Perlu diingat bahwa walaupun ada hubungan antara dua variabel, bukan berarti ada hubungan sebab akibat di antara keduanya, yaitu korelasi antara dua variabel bukan berarti perubahan suatu variabel menjadi penyebab perubahan variabel tersebut. variabel lainnya.

Misalnya, jika kita menemukan adanya hubungan positif antara produksi dua hormon berbeda di dalam tubuh, peningkatan satu hormon tidak harus menyebabkan peningkatan hormon lainnya. Bisa jadi tubuh memproduksi kedua hormon tersebut karena memerlukan keduanya untuk melawan suatu penyakit dan oleh karena itu meningkatkan kadar keduanya secara bersamaan, dalam hal ini penyebabnya adalah penyakit tersebut. Untuk mengetahui apakah terdapat hubungan sebab akibat antara kedua hormon tersebut, perlu dilakukan penelitian lebih lanjut.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya