Apa yang dimaksud dengan tradeoff bias-varians dalam pembelajaran mesin?

Untuk mengevaluasi performa model pada kumpulan data, kita perlu mengukur seberapa cocok prediksi model tersebut dengan data observasi.

Untuk model regresi , metrik yang paling umum digunakan adalah mean square error (MSE), yang dihitung sebagai berikut:

MSE = (1/n)*Σ(y _saya – f(x _saya )) ²

Emas:

• n: jumlah total observasi
• y _i : Nilai respon observasi ^ke-i
• f(x _i ) : Nilai respon prediksi observasi ^ke -i

Semakin dekat prediksi model dengan observasi, maka MSE akan semakin rendah.

Namun, kami hanya peduli dengan pengujian MSE – MSE ketika model kami diterapkan pada data yang tidak terlihat. Hal ini karena kami hanya peduli pada performa model pada data yang tidak diketahui, bukan pada data yang sudah ada.

Misalnya, tidak masalah jika model yang memprediksi harga saham memiliki MSE yang rendah pada data historis, namun kami benar-benar ingin dapat menggunakan model tersebut untuk memprediksi data masa depan secara akurat.

Ternyata tes MSE masih bisa dipecah menjadi dua bagian:

(1) Varians: mengacu pada jumlah perubahan fungsi f jika kita memperkirakannya menggunakan set pelatihan yang berbeda.

(2) Bias: mengacu pada kesalahan yang timbul saat mendekati masalah nyata, yang mungkin sangat rumit, dengan model yang lebih sederhana.

Ditulis dalam istilah matematika:

Tes MSE = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

Uji MSE = Varians + Bias ² + Kesalahan yang tidak dapat direduksi

Istilah ketiga, kesalahan yang tidak dapat direduksi, adalah kesalahan yang tidak dapat dikurangi dengan model apa pun hanya karena selalu ada gangguan dalam hubungan antara himpunan variabel penjelas dan variabel respons .

Model yang memiliki bias tinggi cenderung memiliki varians yang rendah . Misalnya, model regresi linier cenderung memiliki bias yang tinggi (dengan asumsi hubungan linier sederhana antara variabel penjelas dan variabel respons) dan varians yang rendah (estimasi model tidak akan banyak berubah dari sampel ke sampel). yang lain).

Namun model dengan bias rendah cenderung memiliki varians tinggi . Misalnya, model nonlinier yang kompleks cenderung memiliki bias yang rendah (tidak mengasumsikan adanya hubungan tertentu antara variabel penjelas dan variabel respon) dengan variansi yang tinggi (estimasi model dapat berubah secara signifikan dari suatu sampel pembelajaran ke sampel lainnya).

Pertukaran bias-varians

Pertukaran bias-varian mengacu pada pertukaran yang terjadi ketika kita memilih untuk mengurangi bias, yang umumnya meningkatkan varians, atau mengurangi varians, yang umumnya meningkatkan bias.

Grafik berikut menawarkan cara untuk memvisualisasikan trade-off ini:

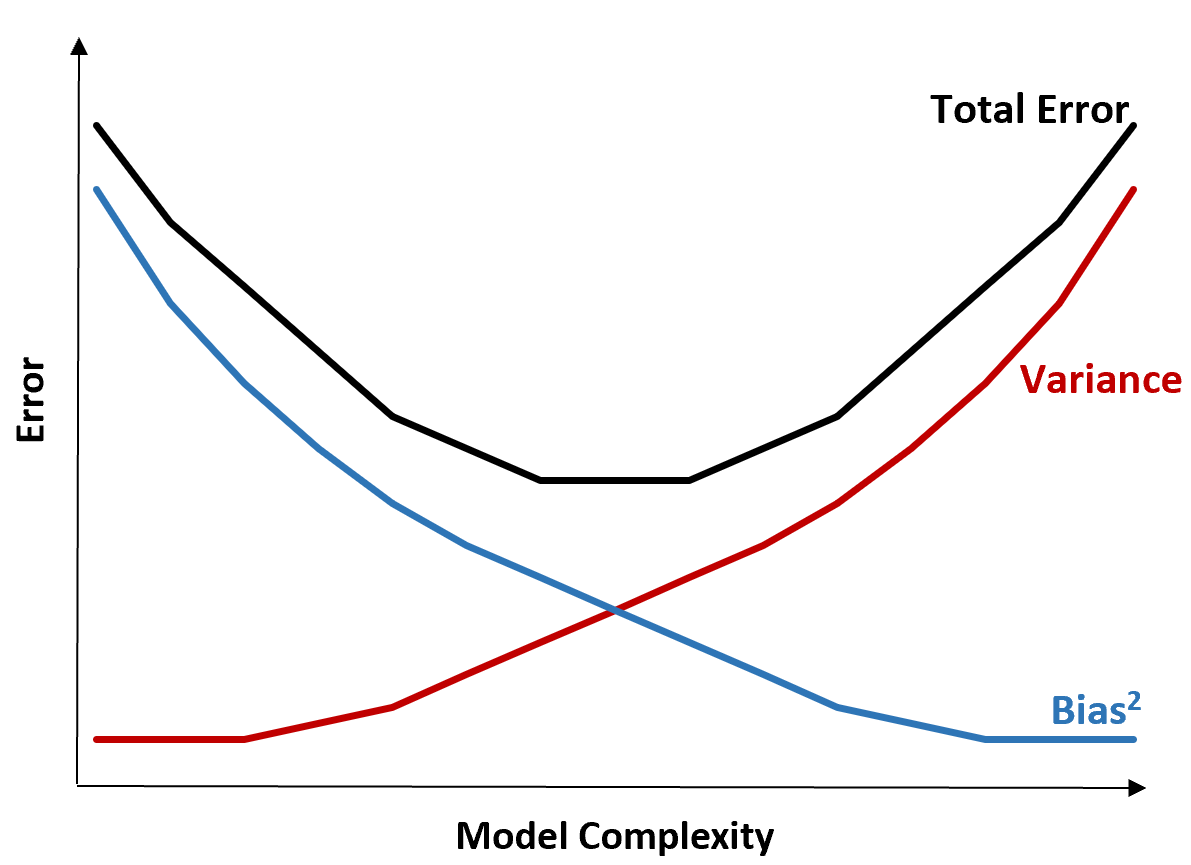
Kesalahan total menurun seiring dengan meningkatnya kompleksitas model, tetapi hanya sampai titik tertentu. Melampaui titik tertentu, varians mulai meningkat dan total error juga mulai meningkat.

Dalam praktiknya, kami hanya peduli untuk meminimalkan kesalahan total suatu model, tidak serta merta meminimalkan varians atau bias. Ternyata cara meminimalkan total error adalah dengan menemukan keseimbangan yang tepat antara varians dan bias.

Dengan kata lain, kita menginginkan model yang cukup kompleks untuk menangkap hubungan sebenarnya antara variabel penjelas dan variabel respon, namun tidak terlalu rumit untuk mendeteksi pola yang sebenarnya tidak ada.

Jika suatu model terlalu rumit, maka model tersebut akan overfits terhadap data. Hal ini terjadi karena terlalu sulit untuk menemukan pola dalam data pelatihan yang hanya disebabkan oleh kebetulan. Model jenis ini cenderung memiliki performa yang buruk pada data yang tidak terlihat.

Namun jika modelnya terlalu sederhana, datanya akan diremehkan . Hal ini terjadi karena diasumsikan bahwa hubungan sebenarnya antara variabel penjelas dan variabel respon lebih sederhana dari yang sebenarnya.

Cara memilih model optimal dalam pembelajaran mesin adalah dengan menemukan keseimbangan antara bias dan varians untuk meminimalkan kesalahan pengujian model pada data yang tidak terlihat di masa mendatang.

Dalam praktiknya, cara paling umum untuk meminimalkan MSE pengujian adalah dengan menggunakan validasi silang .