Koreksi kontinuitas yate: definisi & contoh

Uji independensi chi-square digunakan untuk mengetahui ada atau tidaknya hubungan yang signifikan antara dua variabel kategori.

Pengujian ini menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ : (hipotesis nol) Kedua variabel tersebut independen.
• H ₁ : (hipotesis alternatif) Kedua variabel tersebut tidak independen. (yaitu mereka terkait)

Kami menggunakan rumus berikut untuk menghitung statistik uji Chi-kuadrat x ² untuk pengujian ini:

X ² = Σ(O _saya -E _saya ) ² / E _saya

Emas:

• Σ: adalah simbol mewah yang berarti “jumlah”
• O: nilai yang diamati
• E: nilai yang diharapkan

Pengujian ini mengasumsikan bahwa probabilitas diskrit frekuensi dalam tabel kontingensi dapat didekati dengan distribusi Chi-kuadrat, yang merupakan distribusi kontinu.

Namun asumsi ini cenderung sedikit salah dan statistik pengujian yang dihasilkan cenderung bias ke atas.

Untuk mengoreksi bias ini, kita dapat menerapkan koreksi kontinuitas Yate , yang menerapkan koreksi berikut pada rumus ^X2 :

X ² = Σ(|O _saya -E _saya | – 0,5) ² / E _saya

Kami biasanya hanya menggunakan koreksi ini ketika setidaknya satu sel dalam tabel kontingensi memiliki frekuensi yang diharapkan kurang dari 5.

Contoh : penerapan koreksi kontinuitas Yate

Misalkan kita ingin mengetahui apakah gender dikaitkan dengan preferensi terhadap suatu partai politik atau tidak. Kami mengambil sampel acak sederhana dari 40 pemilih dan menanyakan preferensi partai politik mereka. Berikut tabel hasil surveinya:

Berikut cara melakukan uji independensi chi-kuadrat dengan koreksi kontinuitas Yate:

Nilai yang diamati:

Nilai yang diharapkan:

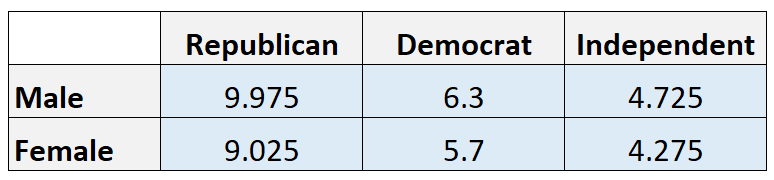
Catatan: Kami menghitung nilai yang diharapkan di setiap sel dengan mengalikan total baris dengan total kolom, lalu membaginya dengan total keseluruhan. Misalnya, perkiraan jumlah anggota Partai Republik adalah (21*19)/40 = 9.975.

_{Statistik uji} ^{chi –} _kuadrat :

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6.3| – 0.5) ² / 6.3 = 0.768
• (|4-4.725| – 0.5) ² / 4.725 = 0.011
• (|11-9.025| – 0.5) ² / 9.025 = 0.241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4.275| – 0.5) ² / 4.275 = 0.012

^Jadi ,

Nilai P: Menurut kalkulator chi-kuadrat ke nilai-P , nilai p yang sesuai dengan statistik uji chi-kuadrat dengan 2 derajat kebebasan adalah 0,3501 .

Karena nilai p ini tidak kurang dari 0,05, kita akan gagal menolak hipotesis nol. Artinya, kami tidak memiliki cukup bukti untuk menyatakan adanya hubungan antara gender dan preferensi partai politik.