Cara menghitung korelasi antara variabel kontinu & kategorikal

Saat kita ingin menghitung korelasi antara dua variabel kontinu, biasanya kita menggunakan koefisien korelasi Pearson .

Namun, ketika kita ingin menghitung korelasi antara variabel kontinu dan variabel kategori , kita dapat menggunakan apa yang disebut korelasi titik biserial .

Korelasi biserial titik digunakan untuk menghitung korelasi antara variabel kategorikal biner (variabel yang hanya dapat mengambil dua nilai) dan variabel kontinu dan memiliki sifat sebagai berikut:

• Korelasi titik-biserial dapat bervariasi antara -1 dan 1.
• Untuk setiap kelompok yang dibuat oleh variabel biner, diasumsikan bahwa variabel kontinu terdistribusi normal dengan varian yang sama.
• Untuk setiap grup yang dibuat oleh variabel biner, diasumsikan tidak ada outlier yang ekstrim.

Contoh berikut menunjukkan cara menghitung korelasi titik-biserial dalam praktiknya.

Contoh: Perhitungan korelasi titik-biserial

Misalkan seorang profesor universitas ingin menentukan apakah ada korelasi antara gender dan nilai pada ujian kualifikasi tertentu.

Dia mengumpulkan data berikut tentang 12 anak laki-laki dan 12 perempuan di kelasnya:

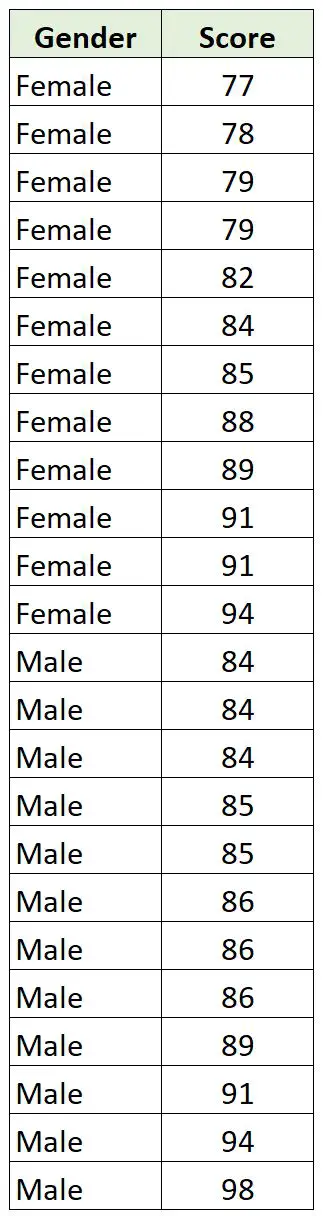
Karena gender merupakan variabel kategorikal dan skor merupakan variabel kontinu, masuk akal untuk menghitung korelasi point-biserial antara kedua variabel.

Profesor dapat menggunakan perangkat lunak statistik apa pun (termasuk Excel, R, Python, SPSS, Stata) untuk menghitung korelasi titik-biserial antara kedua variabel.

Kode berikut menunjukkan cara menghitung korelasi titik-biserial di R, menggunakan nilai 0 untuk mewakili perempuan dan 1 untuk mewakili laki-laki untuk variabel gender:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Dari hasilnya, kita dapat melihat bahwa koefisien korelasi point-biserial adalah 0,281 dan nilai p yang sesuai adalah 0,1833 .

Karena koefisien korelasinya positif, hal ini menunjukkan bahwa ada korelasi positif antara gender dan skor.

Karena kami mengkodekan laki-laki sebagai 1 dan perempuan sebagai 0, hal ini menunjukkan bahwa skor cenderung lebih tinggi untuk laki-laki (yaitu, skor cenderung meningkat seiring dengan “peningkatan” gender). » dari 0 hingga 1).

Namun, karena nilai p tidak kurang dari 0,05, koefisien korelasi ini tidak signifikan secara statistik.

Sumber daya tambahan

Tutorial berikut menjelaskan cara menghitung korelasi titik biserial menggunakan perangkat lunak statistik yang berbeda:

Cara menghitung korelasi titik-biserial di Excel
Cara menghitung korelasi titik-biserial di R
Cara menghitung korelasi titik-biserial dengan Python