Cara menghitung korelasi parsial di excel

Dalam statistik, kita sering menggunakan koefisien korelasi Pearson untuk mengukur hubungan linier antara dua variabel. Namun, terkadang kita ingin memahami hubungan antara dua variabel sambil mengendalikan variabel ketiga .

Misalnya, kita ingin mengukur hubungan antara jumlah jam belajar siswa dan nilai ujian akhir, sambil mengontrol nilai siswa saat ini di kelas. Dalam hal ini, kita dapat menggunakan korelasi parsial untuk mengukur hubungan antara jam belajar dan nilai ujian akhir.

Tutorial ini menjelaskan cara menghitung korelasi parsial di Excel.

Contoh: korelasi parsial di Excel

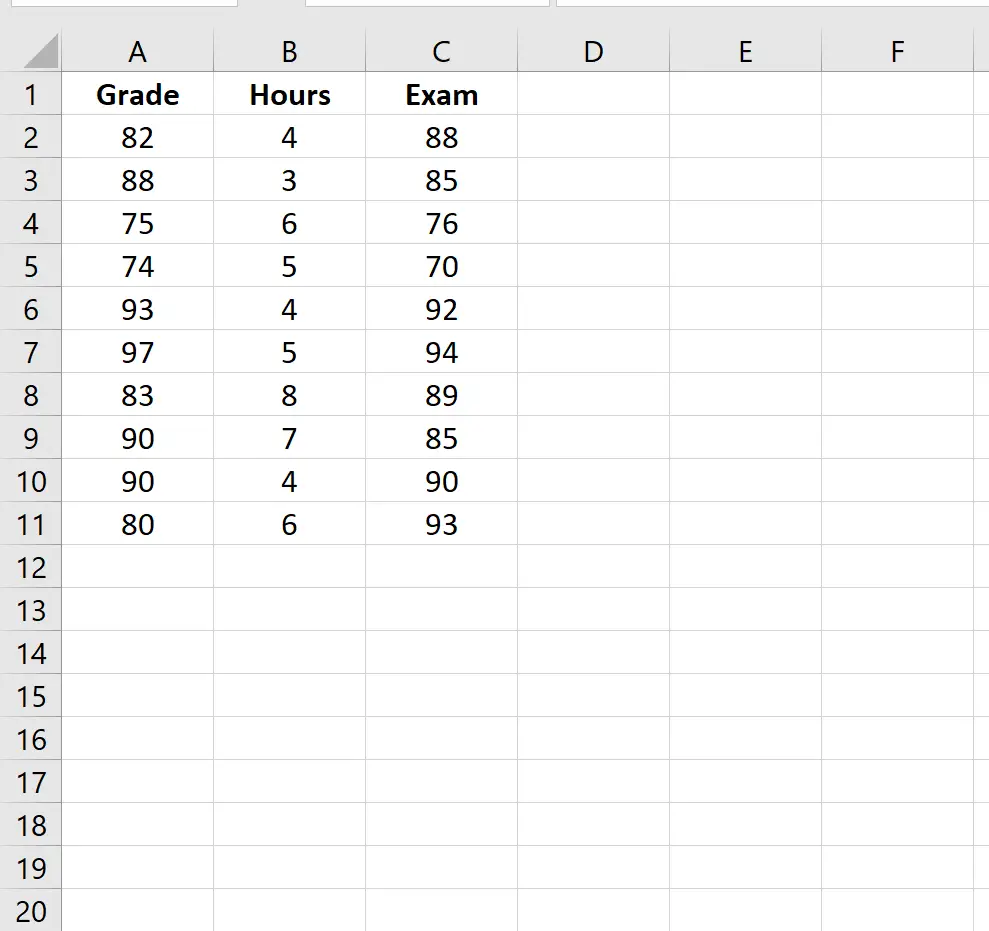
Katakanlah kita memiliki kumpulan data yang menampilkan informasi berikut untuk 10 siswa:

• Nilai saat ini di kelas
• Berjam-jam dihabiskan untuk belajar untuk ujian akhir
• Nilai ujian akhir

Gunakan langkah-langkah berikut untuk menemukan korelasi parsial antara jam belajar dan nilai ujian sambil mengontrol nilai saat ini.

Langkah 1: Hitung setiap korelasi berpasangan.

Pertama, kita akan menghitung korelasi antara setiap kombinasi variabel berpasangan:

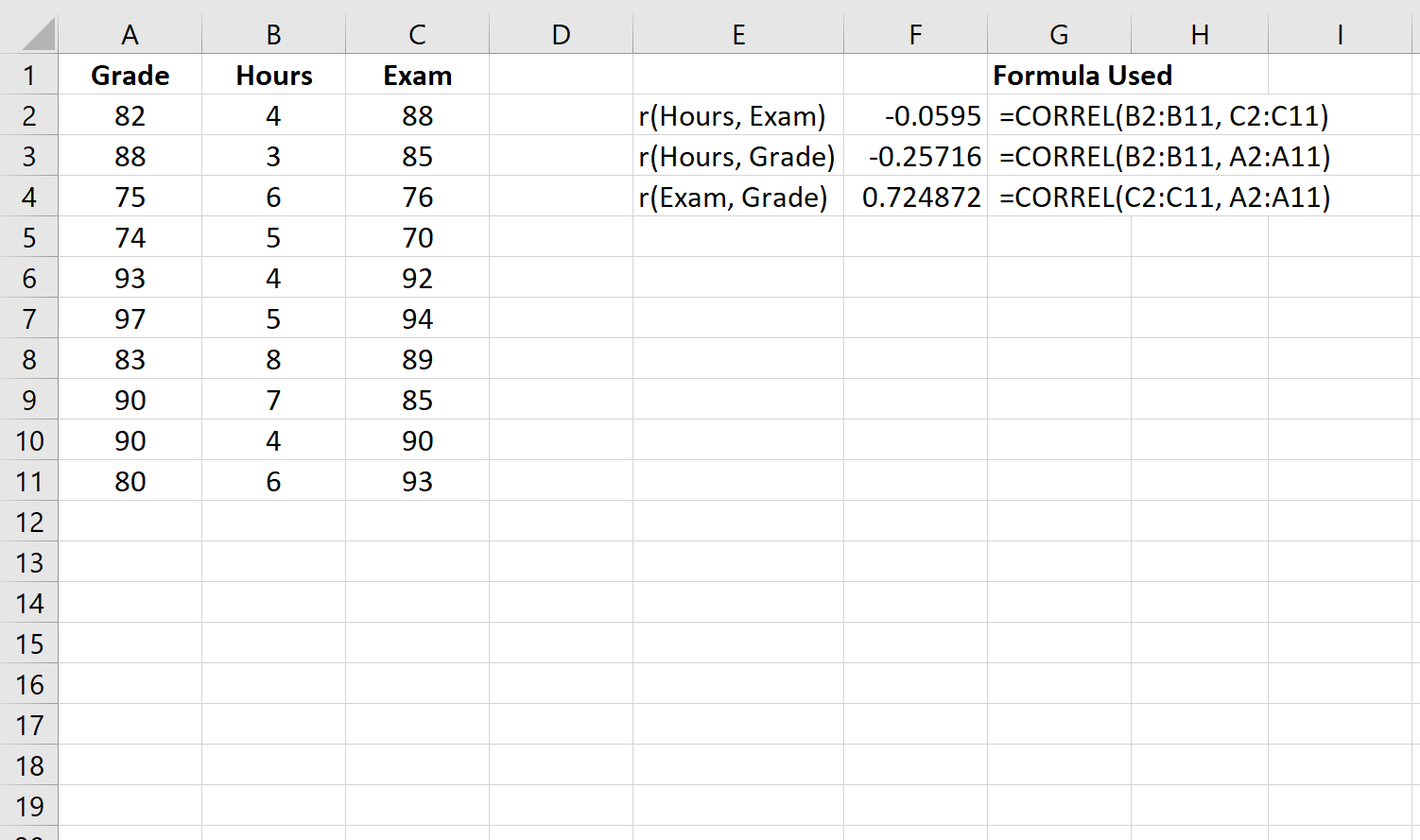
Langkah 2: Hitung korelasi parsial antara jam kerja dan nilai ujian.

Rumus untuk menghitung korelasi parsial antara variabel A dan variabel B sekaligus mengendalikan variabel C adalah sebagai berikut:

Korelasi parsial = (r _A,B – r _A,C *r _B,C ) / √((1-r ² _A,B )(1-r ² _B,C ))

Tangkapan layar berikut menunjukkan cara menggunakan rumus ini untuk menghitung korelasi parsial antara jam kerja dan nilai ujian, dengan mengontrol nilai saat ini:

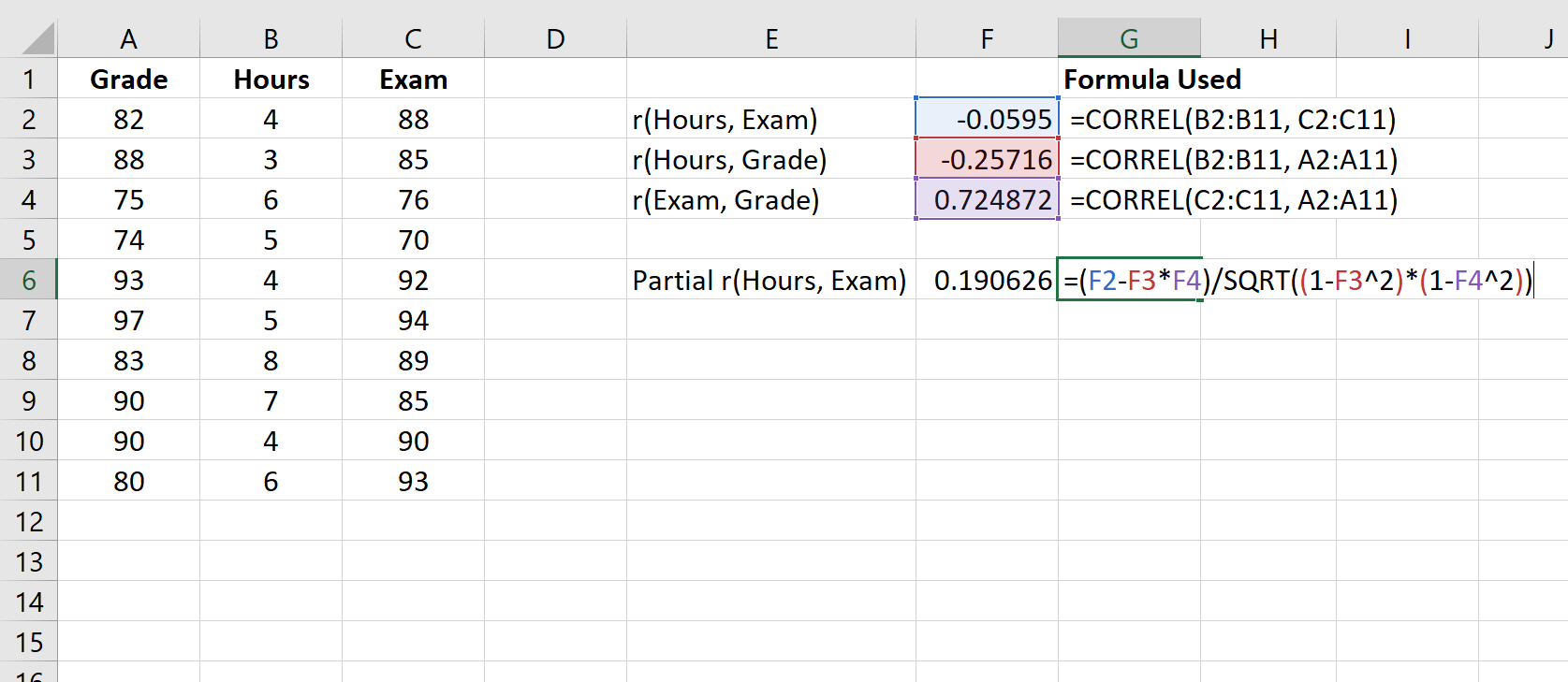
Korelasi parsial sebesar 0,190626 . Untuk menentukan apakah korelasi ini signifikan secara statistik, kita dapat menemukan nilai p yang sesuai.

Langkah 3: Hitung nilai p dari korelasi parsial.

Statistik uji -t dapat dihitung sebagai berikut:

t = r√(n-3) / √(1-r ² )

Tangkapan layar berikut menunjukkan cara menggunakan rumus ini untuk menghitung statistik uji dan nilai p yang sesuai:

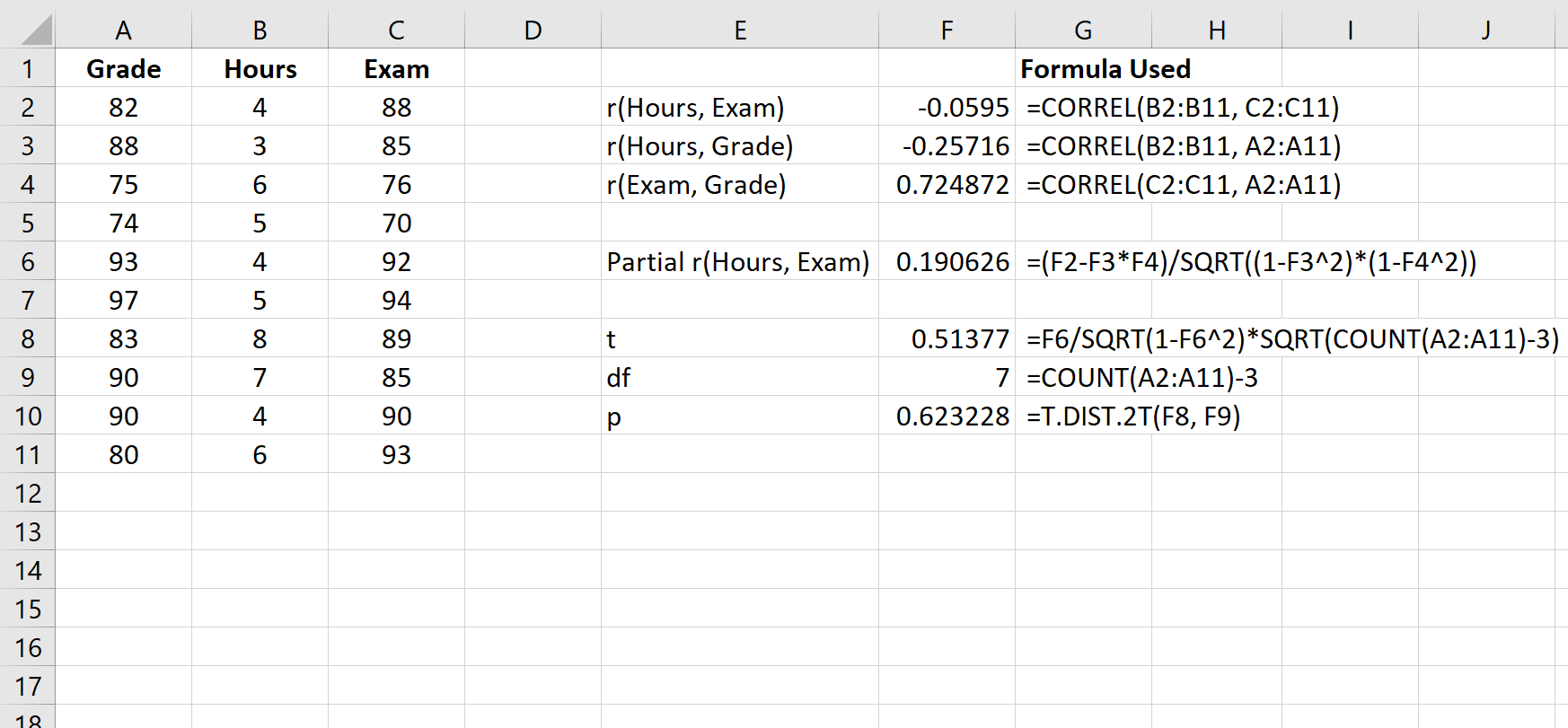
Statistik uji -t sebesar 0,51377 . Jumlah derajat kebebasannya adalah n-3 = 10-3 = 7 . Nilai p yang sesuai adalah 0,623228 . Karena nilai ini tidak kurang dari 0,05, berarti korelasi parsial antara jam kerja dan hasil ujian tidak signifikan secara statistik.