Cara menghitung korelasi rank spearman di google sheets
Dalam statistik, korelasi mengacu pada kekuatan dan arah hubungan antara dua variabel. Nilai koefisien korelasi dapat berkisar antara -1 hingga 1, dengan interpretasi sebagai berikut:
- -1 : hubungan negatif sempurna antara dua variabel
- 0: tidak ada hubungan antara dua variabel
- 1: hubungan positif sempurna antara dua variabel
Jenis korelasi khusus disebut korelasi peringkat Spearman , yang digunakan untuk mengukur korelasi antara dua variabel peringkat. (misalnya, peringkat nilai ujian matematika siswa relatif terhadap peringkat nilai ujian sains di suatu kelas).
Tutorial ini menjelaskan cara menghitung korelasi peringkat Spearman antara dua variabel di Google Sheets.
Contoh: Korelasi Peringkat Spearman di Google Spreadsheet
Lakukan langkah-langkah berikut untuk menghitung korelasi rank spearman antara nilai ujian matematika dengan nilai ujian sains 10 siswa pada suatu kelas tertentu.
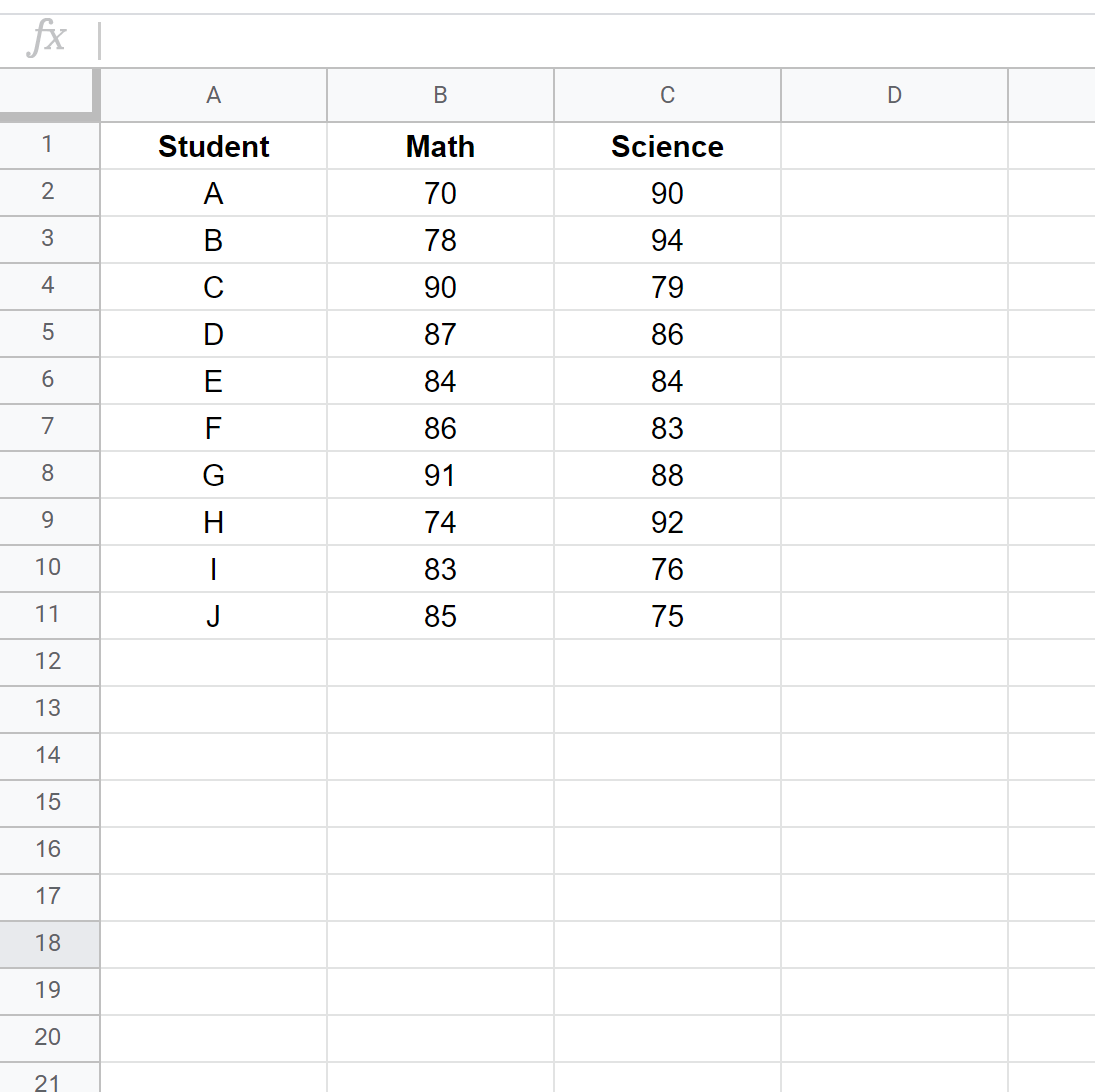
Langkah 1: Masukkan datanya.
Masukkan hasil ujian setiap siswa dalam dua kolom terpisah:
Langkah 2: Hitung peringkat untuk setiap nilai ujian.
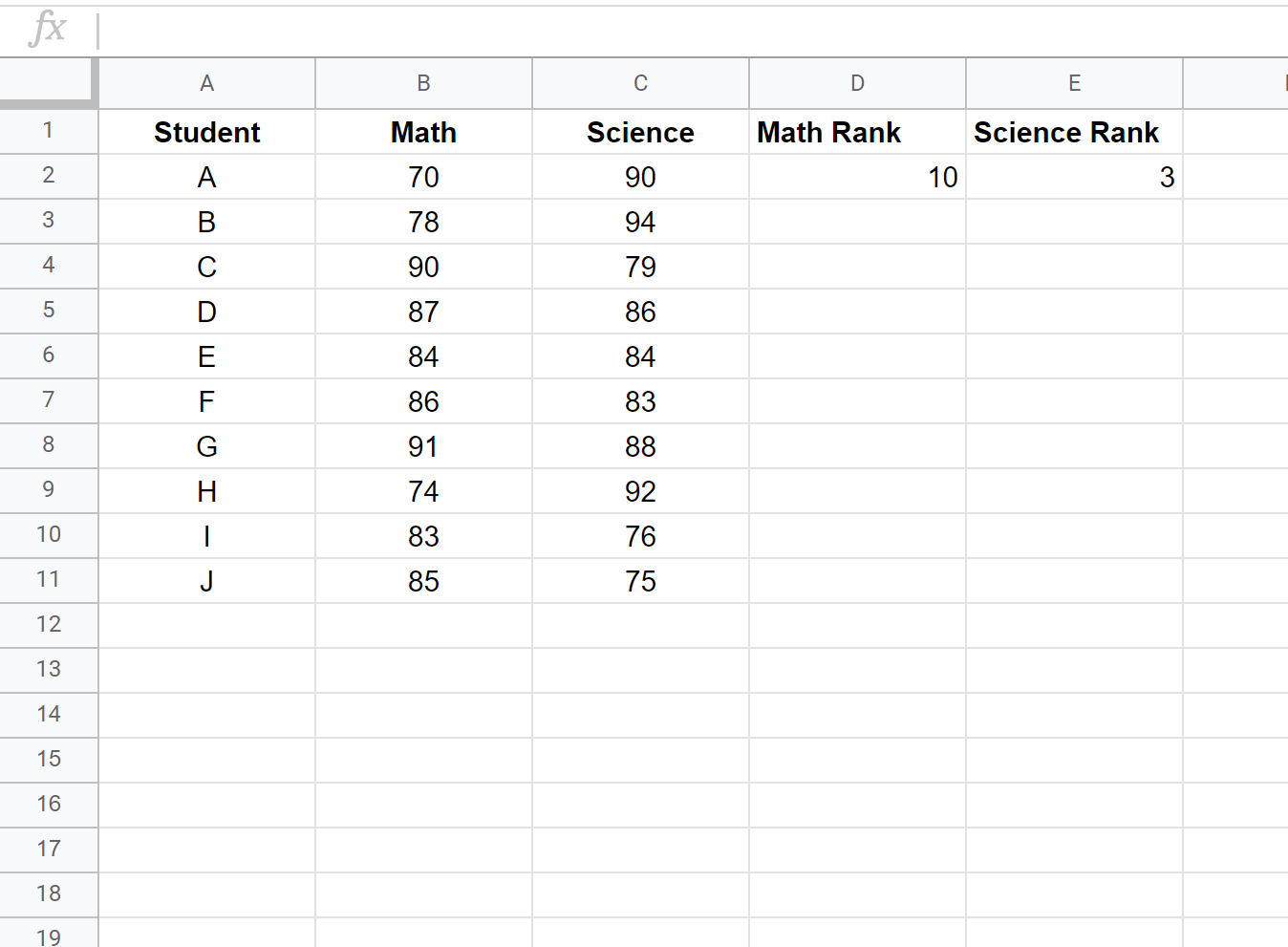
Selanjutnya kita akan menghitung rangking setiap nilai ujian. Gunakan rumus berikut di sel D2 dan E2 untuk menghitung peringkat matematika dan sains siswa pertama:
Sel D2: =RANK.AVG(B2, $B$2:$B$11, 0)
Sel E2: =RANK.AVG(C2, $C$2:$C$11, 0)
Selanjutnya, sorot sel yang tersisa untuk diisi:
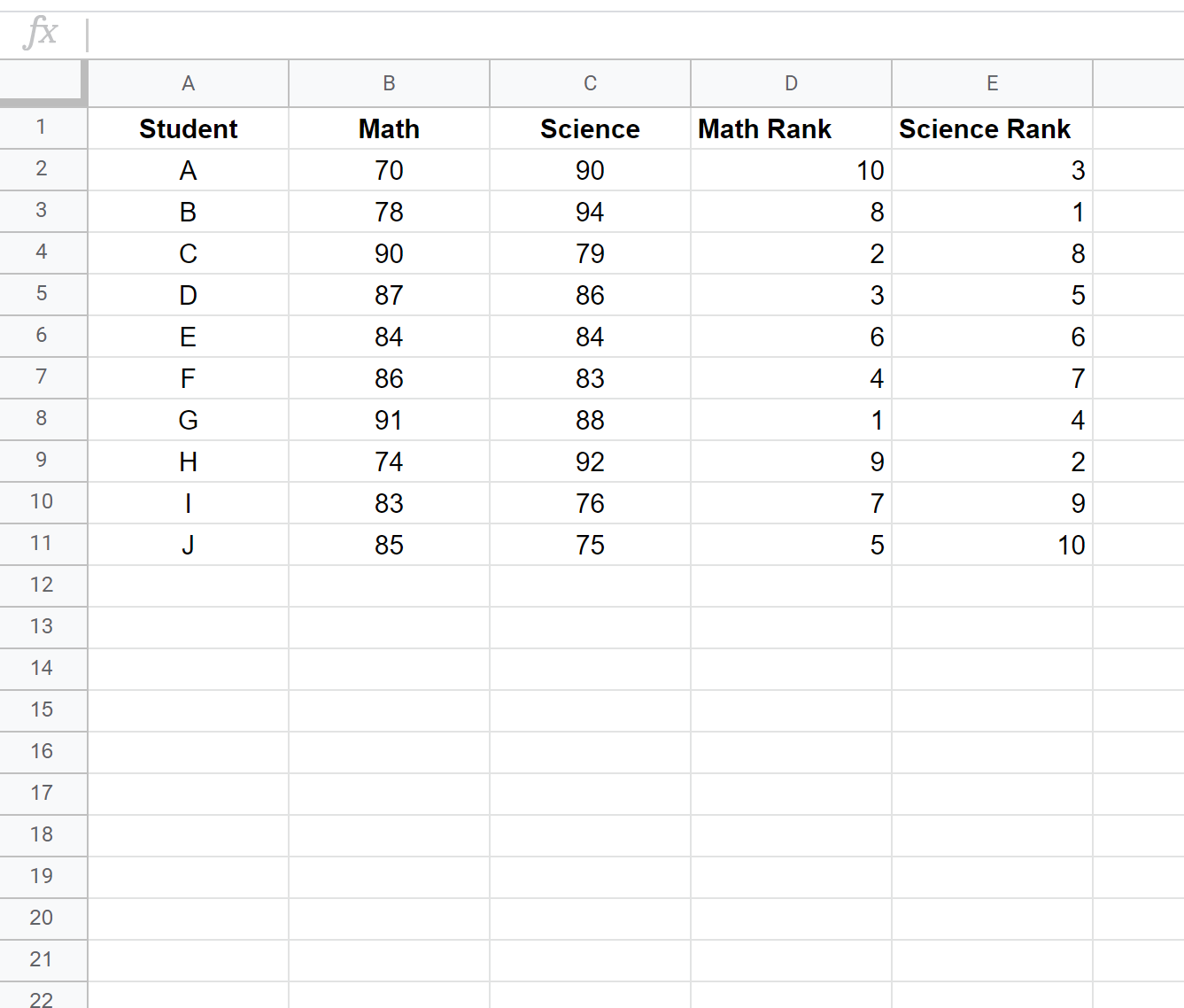
Kemudian klik Ctrl+D untuk memasukkan peringkat setiap siswa:
Langkah 3: Hitung koefisien korelasi peringkat Spearman.
Terakhir, kita akan menghitung koefisien korelasi peringkat Spearman antara nilai matematika dan nilai sains menggunakan fungsi CORREL() :
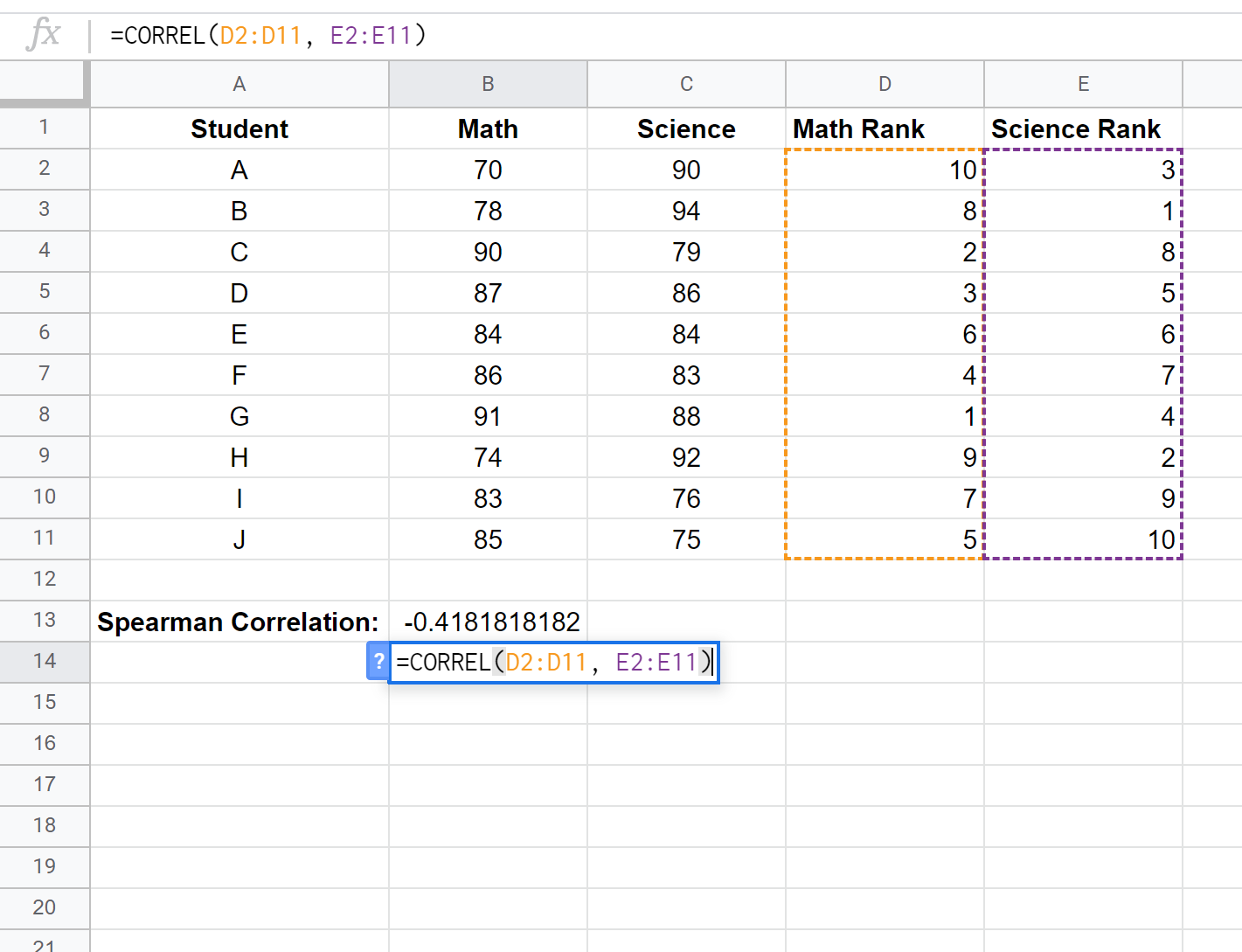
Korelasi peringkat Spearman ternyata -0,41818 .
Langkah 4 (Opsional): Tentukan apakah korelasi peringkat Spearman signifikan secara statistik.
Pada langkah sebelumnya, kami menemukan bahwa korelasi peringkat Spearman antara nilai ujian matematika dan sains adalah -0,41818 , yang menunjukkan korelasi negatif antara kedua variabel.
Namun, untuk menentukan apakah korelasi ini signifikan secara statistik, kita perlu mengacu pada tabel korelasi nilai kritis peringkat Spearman, yang menunjukkan nilai kritis yang terkait dengan ukuran sampel (n) dan tingkat signifikansi (α) yang berbeda.
Jika nilai absolut koefisien korelasi kita lebih besar dari nilai kritis pada tabel, maka korelasi kedua variabel tersebut signifikan secara statistik.
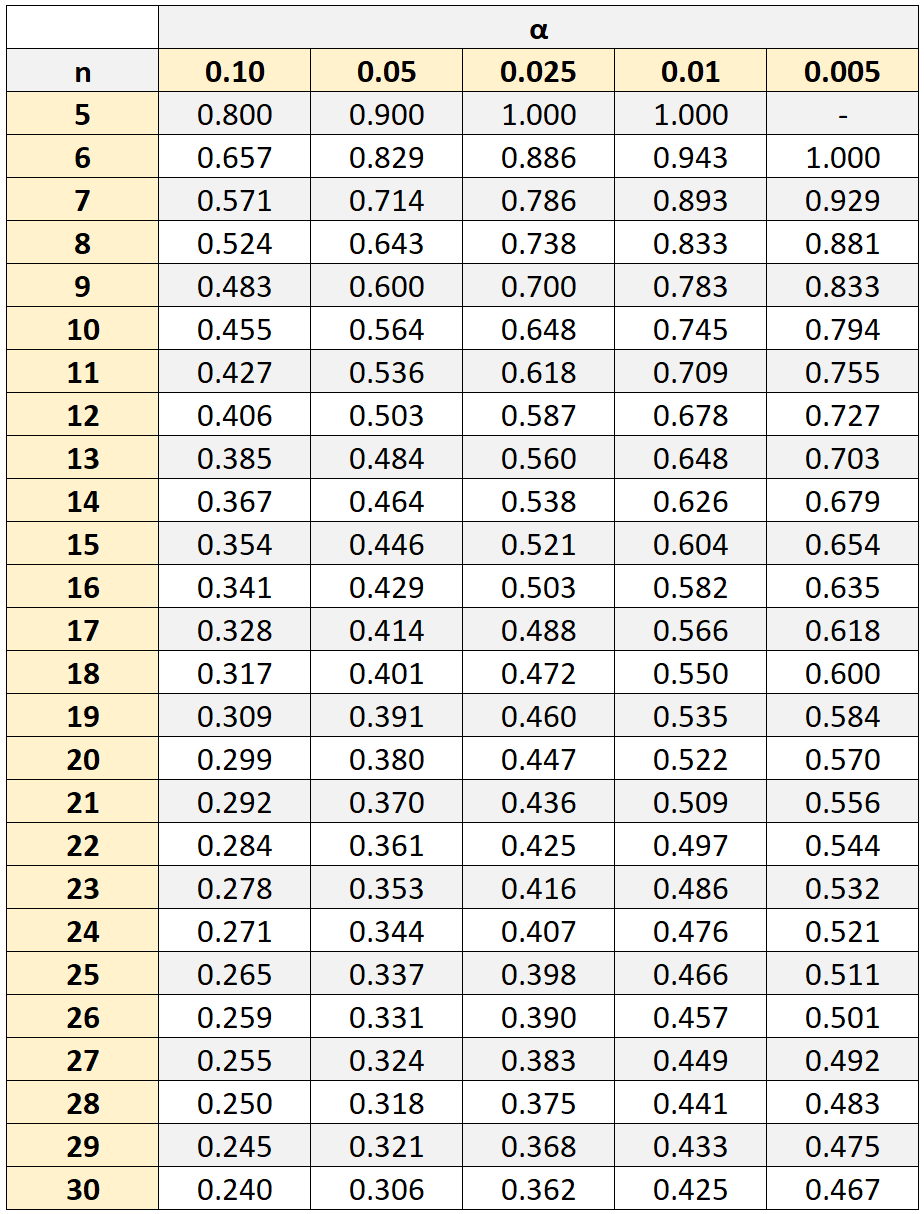
Dalam contoh kita, ukuran sampel kita adalah n = 10 siswa. Dengan menggunakan tingkat signifikansi 0,05, kami menemukan bahwa nilai kritisnya adalah 0,564 .
Karena nilai absolut koefisien korelasi peringkat Spearman yang kami hitung ( 0,41818 ) tidak lebih besar dari nilai kritis ini, ini berarti korelasi antara nilai matematika dan sains tidak signifikan secara statistik.
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya