Kovarian
Artikel ini menjelaskan apa itu kovarians dan cara menghitungnya. Anda akan menemukan rumus kovarians serta contoh penghitungan kovarians suatu kumpulan data. Selain itu, Anda dapat menghitung kovarians rangkaian data apa pun dengan kalkulator online di bagian akhir.
Apa itu kovarians?
Dalam statistik, kovarians adalah nilai yang menunjukkan derajat variasi gabungan dua variabel acak. Dengan kata lain, kovarians digunakan untuk menganalisis ketergantungan antara dua variabel.
Kovariansi sama dengan jumlah hasil kali selisih antara data kedua variabel dan rata-rata masing-masing dibagi dengan jumlah total data.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung kovarians kumpulan data apa pun.
Interpretasi nilai kovarians sangat sederhana:
- Jika kovariansnya positif berarti ada ketergantungan antara kedua variabel. Oleh karena itu, ketika salah satu variabel meningkat nilainya, maka variabel lainnya juga meningkat, begitu pula sebaliknya.
- Jika kovariansnya negatif , berarti hubungan kedua variabel tersebut negatif. Jadi, ketika salah satu variabel meningkat nilainya, maka variabel lainnya menurun, dan sebaliknya.
- Jika kovariansnya nol (atau nilainya mendekati nol), berarti tidak ada hubungan antara kedua variabel. Dengan kata lain, kedua variabel acak tersebut bersifat independen.
Cara menghitung kovarians
Untuk menghitung kovarians suatu seri data, langkah-langkah berikut harus dilakukan:
- Hitung rata-rata setiap variabel secara terpisah.
- Untuk setiap variabel, carilah selisih antara masing-masing nilainya dan mean variabel tersebut.
- Kalikan selisih yang dihitung pada langkah sebelumnya untuk setiap titik data.
- Jumlahkan semua hasil yang diperoleh pada langkah sebelumnya.
- Bagilah dengan jumlah total data. Nilai yang diperoleh merupakan kovarians dari seri data.
Secara ringkas rumus menghitung kovarians antara dua variabel adalah sebagai berikut:
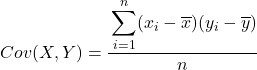
Metode yang sangat disarankan untuk mengekstrak kovarians antara dua variabel adalah dengan membuat tabel berisi semua pasangan data dan menambahkan kolom untuk setiap langkah yang dijelaskan di atas. Dengan cara ini perhitungan Anda akan lebih terorganisir dan Anda akan lebih memahami apa yang Anda lakukan.
Contoh perhitungan kovarians
Mengingat definisi kovarians, berikut adalah contoh langkah demi langkah penghitungan jenis ukuran statistik ini. Tujuannya agar Anda lebih memahami konsep kovarians dan cara menganalisis korelasi dua variabel.
- Hitung kovarians dari kumpulan data statistik berikut:

Pertama, kita perlu menghitung mean aritmatika setiap variabel. Untuk melakukan ini, kita membagi jumlah nilai setiap variabel dengan jumlah total data.
![]()
![]()
Setelah kita menentukan rata-rata setiap variabel acak, kita dapat menambahkan kolom berikut ke tabel data untuk mendapatkan kovariansnya:
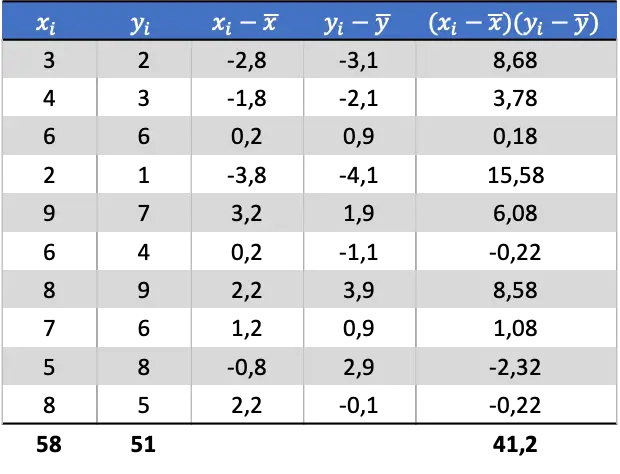
Jadi untuk menentukan kovarians kedua variabel harus membagi jumlah kolom terakhir dengan jumlah pasangan data:
![Rendered by QuickLaTeX.com \begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-49b4992f8443e4d94e38dfa56da38a9a_l3.png)
Dalam hal ini nilai kovariansnya bernilai positif yang berarti terdapat ketergantungan searah antara kedua variabel acak yang diteliti. Namun jika nilai kovariansnya negatif berarti ketergantungan kedua variabel tersebut berbanding terbalik. Dan yang terakhir, jika nilai kovariansnya nol atau sangat mendekati nol, berarti tidak ada hubungan linier antara kedua variabel tersebut.
Seperti yang Anda lihat dari penyelesaian contoh ini, sangat berguna menggunakan program komputer seperti Excel untuk menambahkan kolom ke tabel dan melakukan penghitungan dengan cepat. Jika tidak, dengan menghitung operasi secara manual, diperlukan waktu lebih lama untuk menemukan kovariansnya.
Kalkulator Kovariansi
Masukkan sekumpulan data statistik ke dalam kalkulator berikut untuk menghitung kovarians antara dua variabel. Anda perlu memisahkan pasangan datanya, sehingga pada kotak pertama hanya terdapat nilai satu variabel dan pada kotak kedua hanya terdapat nilai variabel kedua.
Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.
Properti Kovarian
Kovarian memiliki sifat-sifat berikut:
- Kovariansi antara variabel acak dan konstanta adalah nol.
![]()
- Kovariansi suatu variabel dan dirinya sendiri setara dengan varians variabel tersebut.
![]()
- Kovariansi memenuhi sifat simetri, sehingga kovarians variabel X dan Y sama dengan kovarians variabel Y dan X. Urutan variabel tidak mempengaruhi hasil kovarians.
![]()
- Jika variabel dikalikan dengan konstanta, Anda dapat menghitung kovariansnya terlebih dahulu, lalu mengalikan hasilnya dengan konstanta.
![]()
- Menambahkan suku ke variabel tidak mempengaruhi hasil kovarians.
![]()
- Kovariansi antara dua variabel acak terkait dengan ekspektasi matematisnya. Kovariansi antara variabel X dan Y sama dengan ekspektasi matematis hasil kali X dan Y dikurangi hasil kali ekspektasi matematis masing-masing variabel.
![]()
- Saat beroperasi dengan variabel, ekspresi aljabar berikut diisi sehubungan dengan kovarians:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5d429b5bb4e4796cc5b8c73ed0845fa2_l3.png)