Kotak yang lebih rendah

Oleh Benjamin anderson Agustus 2, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa yang dimaksud dengan kuadrat terkecil dalam statistik, apa itu metode kuadrat terkecil, dan bagaimana model regresi disesuaikan dengan kriteria kuadrat terkecil.

Apa metode kuadrat terkecil?

Metode kuadrat terkecil merupakan metode statistik yang digunakan untuk menentukan persamaan regresi. Dengan kata lain, metode kuadrat terkecil merupakan kriteria yang digunakan dalam suatu model regresi untuk meminimalkan kesalahan yang diperoleh pada saat menghitung persamaan regresi.

Konkritnya, metode kuadrat terkecil terdiri dari meminimalkan jumlah kuadrat dari residu, atau dengan kata lain didasarkan pada meminimalkan jumlah kuadrat selisih antara nilai yang diprediksi oleh model regresi dan nilai yang diamati. . . Di bawah ini kita akan melihat secara rinci bagaimana model regresi dilengkapi dengan kriteria kuadrat terkecil.

Fitur utama dari metode kuadrat terkecil adalah jarak terjauh antara nilai yang diamati dan fungsi regresi diminimalkan. Berbeda dengan kriteria regresi lainnya, metode kuadrat terkecil menganggap lebih penting untuk meminimalkan residu yang besar daripada residu yang kecil, karena kuadrat dari suatu bilangan yang besar jauh lebih besar daripada kuadrat dari suatu bilangan yang kecil. nomor.

Kesalahan estimasi

Untuk memahami sepenuhnya konsep kuadrat terkecil, pertama-tama kita harus memahami dengan jelas apa yang dimaksud dengan residu dalam model regresi. Oleh karena itu, di bawah ini kita akan melihat apa itu kesalahan estimasi dan bagaimana cara menghitungnya.

Dalam statistik, kesalahan estimasi , disebut juga residu , adalah selisih antara nilai sebenarnya dan nilai yang sesuai dengan model regresi. Oleh karena itu, residu statistik dihitung sebagai berikut:

$e_i=y_i-\widehat{y}_i$

Emas:

$e_i$

adalah sisa data i.
$y_i$

adalah nilai sebenarnya dari data i.
$\widehat{y}_i$

adalah nilai yang diberikan oleh model regresi untuk data i.

Jadi, semakin besar sisa suatu data, semakin buruk model regresi beradaptasi dengan data tersebut. Jadi, semakin kecil suatu residu, semakin kecil jarak antara nilai sebenarnya dan nilai prediksinya.

Demikian pula, jika sisa suatu data bernilai positif, berarti model regresi memprediksi nilai yang lebih rendah dari nilai sebenarnya. sedangkan jika residunya negatif berarti nilai prediksi lebih besar dari nilai sebenarnya.

Minimalkan kotak kesalahan

Sekarang setelah kita mengetahui apa itu residu dalam statistik, akan lebih mudah untuk memahami bagaimana kuadrat kesalahan diminimalkan.

Kuadrat kesalahan adalah kuadrat sisa, jadi kuadrat kesalahan sama dengan selisih antara nilai sebenarnya dan nilai yang disesuaikan dengan model regresi yang dipangkatkan dua.

$e_i^2=(y_i-\widehat{y}_i)^2$

Emas:

$e_i^2$

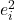
adalah kuadrat dari sisa data i.
$y_i$

adalah nilai sebenarnya dari data i.
$\widehat{y}_i$

adalah nilai yang diberikan oleh model regresi untuk data i.

Jadi, metode kuadrat terkecil terdiri dari pembuatan model regresi dengan meminimalkan jumlah kuadrat kesalahan . Oleh karena itu, kriteria kuadrat terkecil didasarkan pada minimalisasi ekspresi berikut:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

Inilah sebabnya mengapa kriteria kuadrat terkecil disebut juga kriteria kuadrat terkecil.

Seperti yang Anda lihat pada rumus sebelumnya, kriteria kuadrat terkecil lebih mementingkan meminimalkan residu yang besar daripada residu yang kecil. Misalnya, jika residu yang satu bernilai 3 dan residu yang lain bernilai 5, maka kuadratnya masing-masing adalah 9 dan 25, maka kriteria kuadrat terkecil akan memprioritaskan minimalisasi residu kedua sebelum residu pertama.

Penyesuaian kuadrat terkecil

Pemasangan model regresi dengan menggunakan kriteria kuadrat terkecil terdiri dari mencari model regresi yang meminimalkan kuadrat residu. Oleh karena itu, persamaan yang diperoleh dari model regresi adalah persamaan yang kuadrat selisih antara nilai yang diamati dan nilai yang dipasang minimal.

Perhatikan pada contoh berikut bahwa terdapat lebih banyak kriteria untuk membuat model regresi dan, bergantung pada kriteria yang dipilih, persamaan regresinya berbeda.

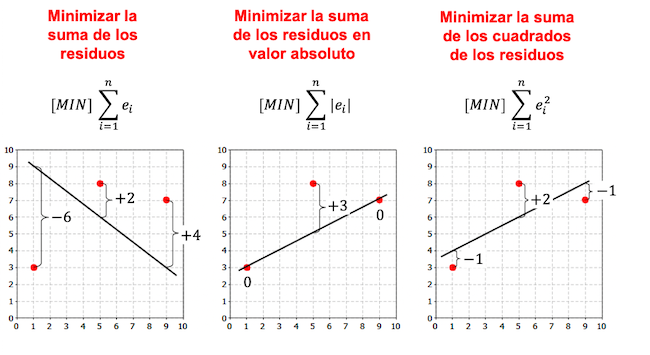
metode kuadrat terkecil, penyesuaian kuadrat terkecil

Seperti yang Anda lihat pada contoh sebelumnya, garis yang diperoleh dari model regresi linier untuk kumpulan data yang sama bergantung pada kriteria yang dipilih. Umumnya, kriteria kuadrat terkecil digunakan dalam model regresi.

Dalam ilmu statistika, model regresi yang paling banyak digunakan adalah model regresi linier sederhana, yaitu pendekatan hubungan antara variabel bebas X dan variabel terikat Y dengan menggunakan garis lurus.

$y=b_0+b_1x$

Jadi, rumus untuk menyesuaikan kumpulan data ke model regresi linier sederhana adalah:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Anda dapat melihat contoh cara menghitung model regresi linier sederhana menggunakan kriteria kuadrat terkecil dengan mengklik link berikut:

➤ Lihat: Contoh regresi linier sederhana

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya