Kuadrat terkecil parsial di r (langkah demi langkah)

Salah satu masalah paling umum yang akan Anda temui dalam pembelajaran mesin adalah multikolinearitas . Hal ini terjadi ketika dua atau lebih variabel prediktor dalam kumpulan data berkorelasi tinggi.

Jika hal ini terjadi, suatu model mungkin dapat menyesuaikan dengan kumpulan data pelatihan dengan baik, namun model tersebut mungkin memiliki performa yang buruk pada kumpulan data baru yang belum pernah dilihatnya karena model tersebut terlalu cocok dengan kumpulan data pelatihan. perlengkapan latihan.

Salah satu cara untuk mengatasi masalah ini adalah dengan menggunakan metode yang disebut kuadrat terkecil parsial , yang cara kerjanya sebagai berikut:

• Standarisasi variabel prediktor dan respons.
• Hitung M kombinasi linier (disebut “komponen PLS”) dari p variabel prediktor asli yang menjelaskan sejumlah besar variasi baik dalam variabel respons maupun variabel prediktor.
• Gunakan metode kuadrat terkecil untuk menyesuaikan model regresi linier menggunakan komponen PLS sebagai prediktor.
• Gunakan validasi silang k-fold untuk menemukan jumlah komponen PLS yang optimal untuk dipertahankan dalam model.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan kuadrat terkecil parsial di R.

Langkah 1: Muat paket yang diperlukan

Cara termudah untuk melakukan kuadrat terkecil parsial di R adalah dengan menggunakan fungsi dalam paket tolong .

 #install pls package (if not already installed)
install.packages(" pls ")

load pls package
library(pls)

Langkah 2: Pasangkan model kuadrat terkecil parsial

Untuk contoh ini, kita akan menggunakan kumpulan data R bawaan yang disebut mtcars yang berisi data tentang berbagai jenis mobil:

 #view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1

Untuk contoh ini, kita akan menyesuaikan model kuadrat terkecil parsial (PLS) dengan menggunakan hp sebagai variabel respons dan variabel berikut sebagai variabel prediktor:

• mpg
• menampilkan
• kotoran
• berat
• qdetik

Kode berikut menunjukkan cara menyesuaikan model PLS dengan data ini. Perhatikan argumen berikut:

• scale=TRUE : Ini memberi tahu R bahwa setiap variabel dalam kumpulan data harus diskalakan agar memiliki rata-rata 0 dan deviasi standar 1. Hal ini memastikan bahwa tidak ada variabel prediktor yang memiliki pengaruh terlalu besar dalam model jika diukur dalam satuan yang berbeda.
• validation=”CV” : Ini memberitahu R untuk menggunakan validasi k-fold cross untuk mengevaluasi kinerja model. Perhatikan bahwa ini menggunakan k=10 lipatan secara default. Perhatikan juga bahwa Anda dapat menentukan “LOOCV” untuk melakukan validasi silang Leave-One-Out .

 #make this example reproducible
set.seed(1)

#fit PCR model
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")

Langkah 3: Pilih jumlah komponen PLS

Setelah kita memasang modelnya, kita perlu menentukan berapa banyak komponen PLS yang harus disimpan.

Untuk melakukannya, cukup lihat uji root mean square error (uji RMSE) yang dihitung dengan validasi k-cross:

 #view summary of model fitting
summary(model)

Data: 
	Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20

TRAINING: % variance explained
    1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03

Hasilnya ada dua tabel menarik:

1. VALIDASI: RMSEP

Tabel ini menunjukkan pengujian RMSE yang dihitung dengan validasi k-fold cross. Kita dapat melihat hal berikut:

• Jika kita hanya menggunakan istilah asli dalam model, RMSE pengujiannya adalah 69.66 .
• Jika kita menambahkan komponen PLS pertama, pengujian RMSE turun menjadi 40,57.
• Jika kita menambahkan komponen PLS kedua, pengujian RMSE turun menjadi 35,48.

Kita dapat melihat bahwa menambahkan komponen PLS tambahan sebenarnya menghasilkan peningkatan RMSE pengujian. Oleh karena itu, tampaknya optimal jika hanya menggunakan dua komponen PLS pada model akhir.

2. PELATIHAN: % varians dijelaskan

Tabel ini menunjukkan persentase varians dalam variabel respon yang dijelaskan oleh komponen PLS. Kita dapat melihat hal berikut:

• Dengan hanya menggunakan komponen PLS pertama, kita dapat menjelaskan 68,66% variasi variabel respon.
• Dengan menambahkan komponen PLS kedua, kita dapat menjelaskan 89,27% variasi variabel respon.

Perhatikan bahwa kita masih dapat menjelaskan lebih banyak varians dengan menggunakan lebih banyak komponen PLS, namun kita dapat melihat bahwa menambahkan lebih dari dua komponen PLS sebenarnya tidak terlalu meningkatkan persentase varians yang dijelaskan.

Kita juga dapat memvisualisasikan pengujian RMSE (bersama dengan pengujian MSE dan R-squared) sebagai fungsi dari jumlah komponen PLS menggunakan fungsi validationplot() .

 #visualize cross-validation plots
validationplot(model)
validationplot(model, val.type=" MSEP ")
validationplot(model, val.type=" R2 ") 

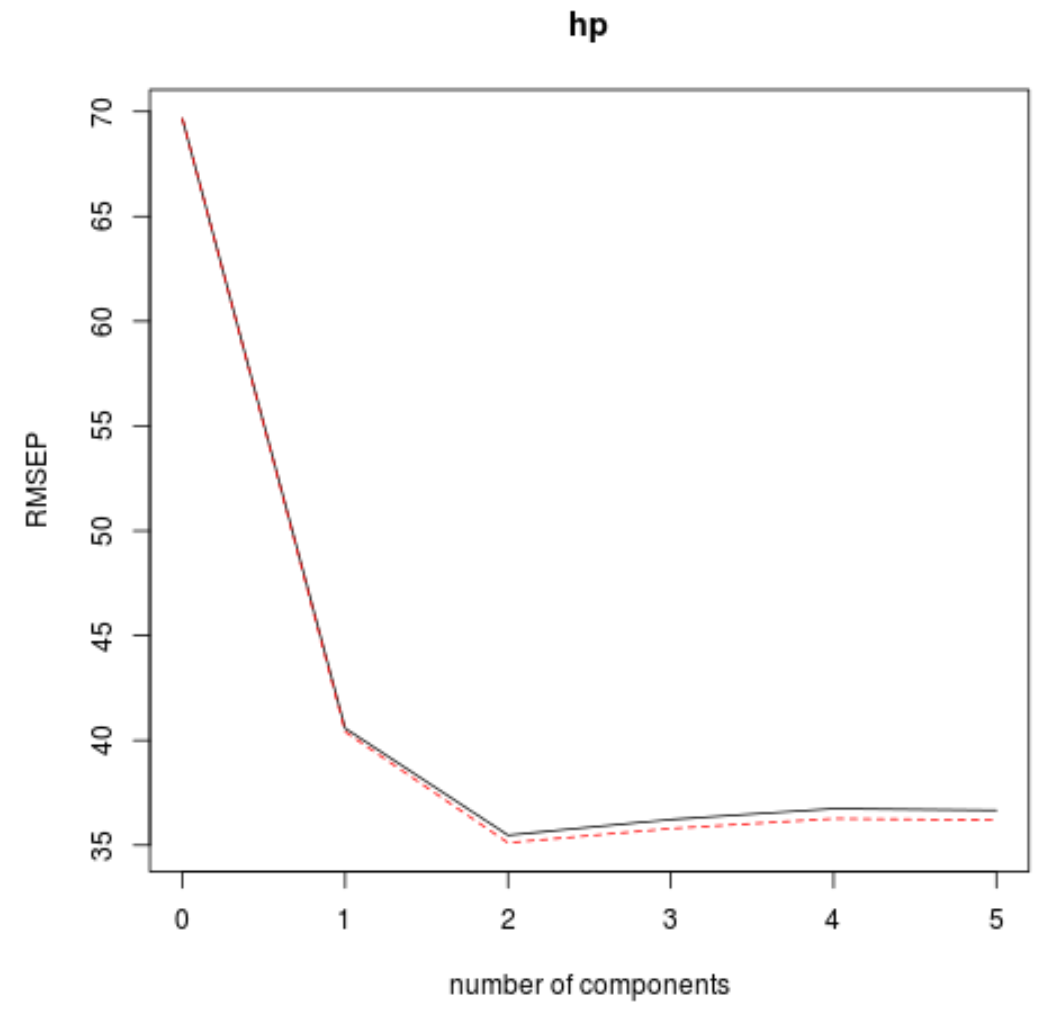
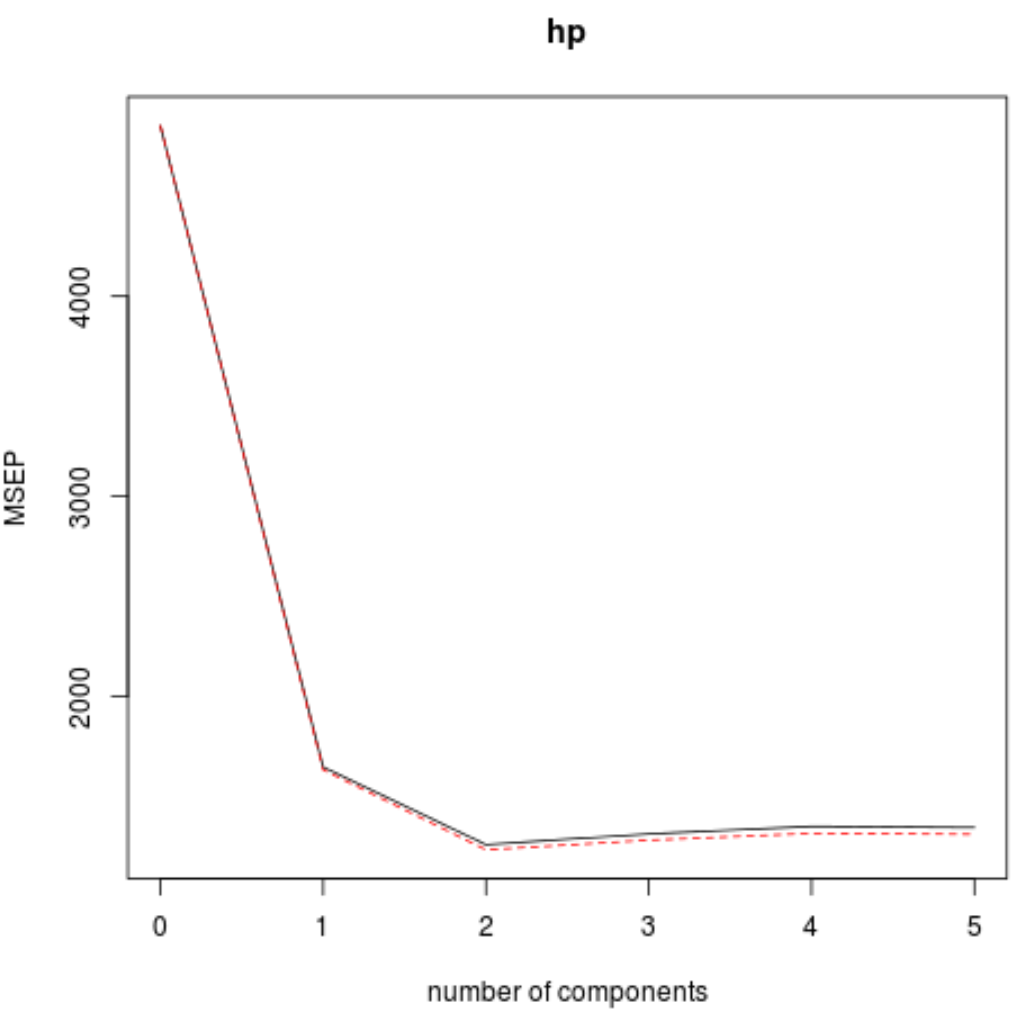
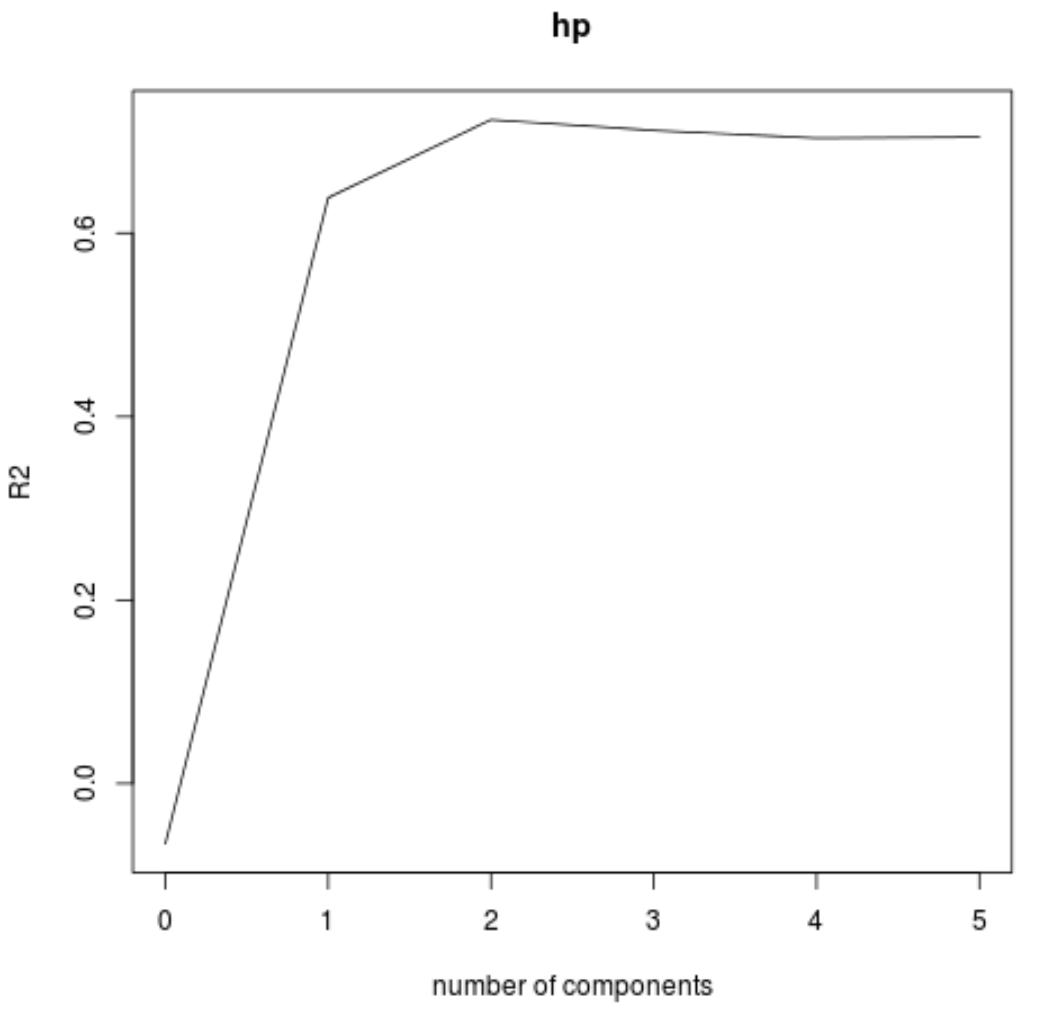
Di setiap grafik, kita dapat melihat bahwa kecocokan model meningkat dengan menambahkan dua komponen PLS, namun cenderung memburuk ketika kita menambahkan lebih banyak komponen PLS.

Dengan demikian, model optimal hanya mencakup dua komponen PLS pertama.

Langkah 4: Gunakan model akhir untuk membuat prediksi

Kita dapat menggunakan model akhir dengan dua komponen PLS untuk membuat prediksi mengenai observasi baru.

Kode berikut menunjukkan cara membagi kumpulan data asli menjadi kumpulan pelatihan dan pengujian serta menggunakan model akhir dengan dua komponen PLS untuk membuat prediksi pada kumpulan pengujian.

 #define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26: nrow (mtcars), c("hp")]
test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ")
pcr_pred <- predict(model, test, ncomp= 2 )

#calculate RMSE
sqrt ( mean ((pcr_pred - y_test)^2))

[1] 54.89609

Kita melihat bahwa RMSE pengujian tersebut ternyata 54.89609 . Ini adalah deviasi rata-rata antara nilai hp yang diprediksi dan nilai hp yang diamati untuk observasi set pengujian.

Perhatikan bahwa model regresi komponen utama yang setara dengan dua komponen utama menghasilkan RMSE pengujian sebesar 56.86549 . Oleh karena itu, model PLS sedikit mengungguli model PCR untuk kumpulan data ini.

Penggunaan penuh kode R dalam contoh ini dapat ditemukan di sini .