Bagaimana melakukan regresi kuadrat terkecil tertimbang di r

Salah satu asumsi utama regresi linier adalah bahwa residu terdistribusi dengan varian yang sama di setiap tingkat variabel prediktor. Asumsi ini dikenal dengan istilah homoskedastisitas .

Jika asumsi ini tidak dipenuhi, maka dikatakan terdapat heteroskedastisitas pada residu. Jika hal ini terjadi, hasil regresi menjadi tidak dapat diandalkan.

Salah satu cara untuk mengatasi masalah ini adalah dengan menggunakan regresi kuadrat terkecil tertimbang , yang memberikan bobot pada observasi sedemikian rupa sehingga observasi dengan varian kesalahan rendah menerima bobot lebih karena berisi lebih banyak informasi dibandingkan dengan observasi dengan varian kesalahan lebih besar.

Tutorial ini memberikan contoh langkah demi langkah tentang cara melakukan regresi kuadrat terkecil tertimbang di R.

Langkah 1: Buat datanya

Kode berikut membuat kerangka data yang berisi jumlah jam belajar dan nilai ujian yang sesuai untuk 16 siswa:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Langkah 2: Lakukan Regresi Linier

Selanjutnya, kita akan menggunakan fungsi lm() agar sesuai dengan model regresi linier sederhana yang menggunakan jam sebagai variabel prediktor dan skor sebagai variabel respons :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Langkah 3: Uji heteroskedastisitas

Selanjutnya, kita akan membuat plot dari residu dan nilai yang dipasang untuk memeriksa heteroskedastisitas secara visual:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

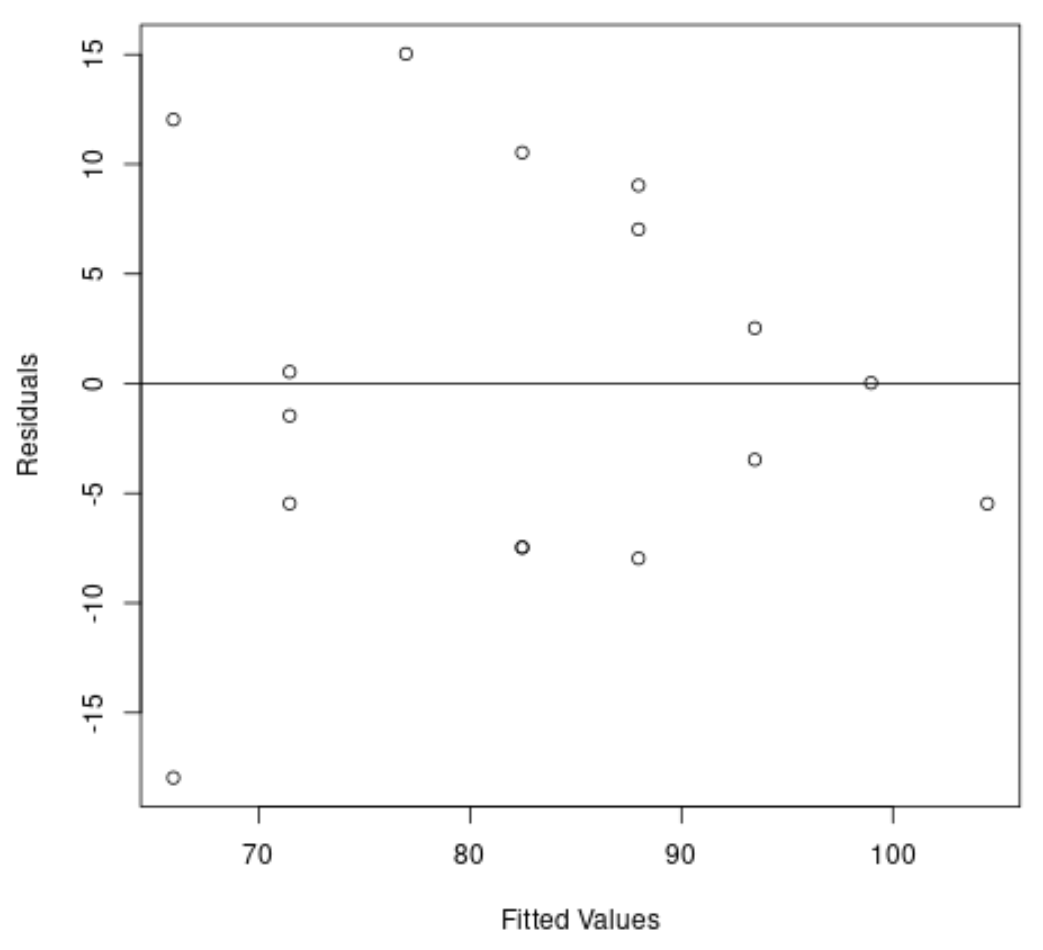
Kita dapat melihat dari grafik bahwa residu berbentuk “kerucut”: residu tidak terdistribusi dengan varian yang sama di seluruh grafik.

Untuk menguji secara formal heteroskedastisitas, kita dapat melakukan uji Breusch-Pagan:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Uji Breusch-Pagan menggunakan hipotesis nol dan hipotesis alternatif berikut:

• Hipotesis nol (H ₀ ): terdapat homoskedastisitas (residu terdistribusi dengan varian yang sama)
• Hipotesis alternatif ( _HA ): terdapat heteroskedastisitas (sisa tidak terdistribusi dengan varian yang sama)

Karena nilai p dari pengujian ini adalah 0,0466 , kami akan menolak hipotesis nol dan menyimpulkan bahwa heteroskedastisitas adalah masalah dalam model ini.

Langkah 4: Lakukan regresi kuadrat terkecil tertimbang

Karena terdapat heteroskedastisitas, kita akan melakukan kuadrat terkecil tertimbang dengan menetapkan bobot sedemikian rupa sehingga pengamatan dengan varians lebih rendah menerima bobot lebih banyak:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

Dari hasil tersebut, kita dapat melihat bahwa estimasi koefisien untuk variabel prediktor jam kerja sedikit berubah dan kesesuaian model secara keseluruhan meningkat.

Model kuadrat terkecil tertimbang memiliki kesalahan standar sisa sebesar 1,199 , dibandingkan dengan 9,224 pada model regresi linier sederhana asli.

Hal ini menunjukkan bahwa nilai prediksi yang dihasilkan oleh model kuadrat terkecil tertimbang jauh lebih mendekati pengamatan sebenarnya dibandingkan dengan nilai prediksi yang dihasilkan oleh model regresi linier sederhana.

Model kuadrat terkecil tertimbang juga memiliki R-kuadrat sebesar 0,6762 , dibandingkan dengan 0,6296 pada model regresi linier sederhana asli.

Hal ini menunjukkan bahwa model kuadrat terkecil tertimbang lebih mampu menjelaskan varians nilai ujian dibandingkan model regresi linier sederhana.

Pengukuran ini menunjukkan bahwa model kuadrat terkecil tertimbang memberikan kesesuaian yang lebih baik terhadap data dibandingkan dengan model regresi linier sederhana.

Sumber daya tambahan

Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi kuantil di R