Kualitas kecocokan
Artikel ini menjelaskan apa yang dimaksud dengan good of fit dalam statistik. Demikian pula, ini menunjukkan cara mengukur goodness of fit model regresi dan, sebagai tambahan, Anda akan dapat melihat penyelesaian penerapan goodness of fit.
Apa yang dimaksud dengan kebaikan kecocokan?
Dalam statistik, goodness of fit adalah seberapa cocok suatu model regresi dengan sampel data. Dengan kata lain, goodness of fit suatu model regresi mengacu pada tingkat kesesuaian antara kumpulan observasi dan nilai yang diperoleh melalui regresi.
Oleh karena itu, semakin baik goodness of fit suatu model regresi, maka semakin baik pula penjelasan data yang diteliti. Oleh karena itu, kami ingin semakin cocok model statistiknya, semakin baik.
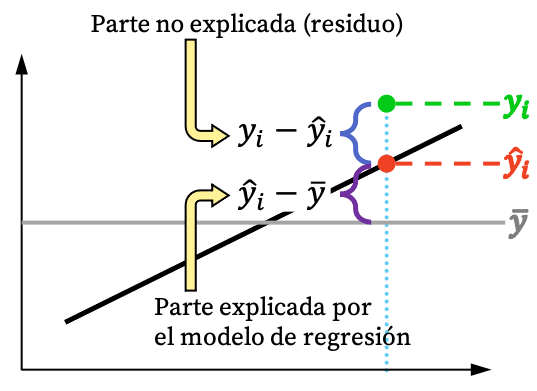
Seperti yang terlihat pada gambar di atas, nilai suatu observasi biasanya tidak dapat dijelaskan sepenuhnya oleh model regresi. Namun secara logis, semakin banyak model regresi yang dapat dijelaskan dari kumpulan data, semakin baik kesesuaian model tersebut. Singkatnya, kami tertarik pada model regresi yang seketat mungkin.
Kesesuaian model regresi
Untuk menentukan goodness of fit suatu model regresi, biasanya digunakan koefisien determinasi , yaitu koefisien statistik yang menunjukkan persentase yang dijelaskan oleh model regresi. Dengan demikian, semakin tinggi koefisien determinasi suatu model, maka semakin baik model tersebut beradaptasi dengan data sampel.
![]()
Namun perlu diperhatikan bahwa semakin banyak variabel yang dimiliki suatu model regresi, maka koefisien determinasinya akan semakin tinggi. Oleh karena itu, koefisien determinasi yang disesuaikan juga sering digunakan untuk mengukur goodness of fit suatu model. Koefisien determinasi yang disesuaikan merupakan variasi dari koefisien sebelumnya yang menunjukkan persentase yang dijelaskan oleh model regresi, memberikan sanksi untuk setiap variabel penjelas yang dimasukkan dalam model.
![]()
Oleh karena itu sebaiknya menggunakan koefisien determinasi yang disesuaikan untuk membandingkan dua model dengan sejumlah variabel yang berbeda, karena memperhitungkan jumlah variabel yang dimasukkan dalam model.
Terakhir, perlu diperhatikan bahwa uji Chi-kuadrat juga dapat digunakan untuk mengukur goodness of fit suatu model regresi, meskipun nilai dari dua koefisien sebelumnya biasanya digunakan.
Contoh nyata dari kecocokan yang baik
Terakhir, kita akan melihat penyelesaian penyelesaian kualitas penyesuaian untuk menyelesaikan asimilasi konsep statistik ini.
- Dengan seri data yang sama dilakukan dua model regresi linier yang berbeda, yang hasilnya dapat Anda lihat pada tabel berikut. Model mana yang terbaik untuk digunakan?
| Model regresi 1 | Model regresi 2 | |
|---|---|---|
| Koefisien determinasi | 57% | 64% |
| Koefisien determinasi yang disesuaikan | 49% | 43% |
| Jumlah variabel penjelas | 3 | 7 |
Dalam hal ini, kami berasumsi bahwa kedua model memenuhi asumsi model regresi linier sebelumnya dan oleh karena itu, kami hanya perlu menganalisis goodness of fit model tersebut.
Model regresi 2 memiliki koefisien determinasi yang lebih tinggi dibandingkan model regresi 1, sehingga nampaknya model regresi lebih baik secara apriori karena mampu menjelaskan data sampel dengan lebih baik.
Namun Model Regresi 2 memiliki 7 variabel independen dalam modelnya, sedangkan Model Regresi 1 hanya memiliki 3 variabel. Jadi Model 2 akan jauh lebih rumit dan sulit untuk diinterpretasikan dibandingkan model pertama.
Selain itu, jika dilihat dari koefisien determinasi yang disesuaikan dengan memperhitungkan jumlah variabel dalam model, model regresi 1 memiliki koefisien determinasi yang disesuaikan lebih tinggi dibandingkan model regresi 2.
Kesimpulannya, meskipun lebih baik menggunakan model regresi 1, karena koefisien determinasi yang disesuaikan lebih tinggi dibandingkan dengan model regresi 2. Model regresi 2 memiliki koefisien determinasi yang tidak disesuaikan lebih tinggi, hal ini disebabkan karena memasukkan lebih banyak variabel dalam regresi. model 1. model, yang meningkatkan nilai koefisien tersebut tetapi mempersulit interpretasi model dan tentunya memperburuk prediksi nilai baru.
Untuk membandingkan model dengan jumlah variabel yang berbeda, yang terbaik adalah menggunakan koefisien determinasi yang disesuaikan karena akan memberikan penalti untuk setiap variabel yang ditambahkan ke model. Seperti yang Anda lihat pada contoh ini, menurut koefisien determinasi yang tidak disesuaikan, model regresi 2 lebih baik, namun melalui koefisien determinasi yang disesuaikan kita dapat mengetahui bahwa model regresi 1 sebenarnya lebih baik.