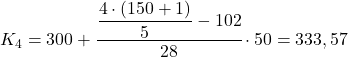Kuintil (statistik)

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Pada artikel ini kami menjelaskan apa itu kuintil dan cara menghitungnya. Anda akan menemukan beberapa contoh penyelesaian penghitungan kuintil dan, sebagai tambahan, Anda akan dapat menghitung kuintil dari sampel statistik apa pun dengan kalkulator online.

Apa itu kuintil?

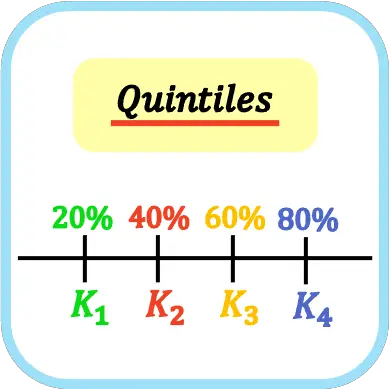
Dalam statistik, kuintil adalah empat nilai yang membagi kumpulan data menjadi lima bagian yang sama. Jadi, kuintil pertama, kedua, ketiga, dan keempat masing-masing mewakili 20%, 40%, 60%, dan 80% data sampel.

Artinya, nilai kuintil ketiga, misalnya, lebih tinggi dari 60% seluruh data yang dikumpulkan, namun lebih rendah dari data lainnya.

Lambang kuintil adalah huruf kapital K dengan indeks kuintil, yakni kuintil pertama adalah K ₁ , kuintil kedua adalah K ₂ , kuintil ketiga adalah K ₃ , dan kuintil keempat adalah K ₄ . Meskipun bisa juga dilambangkan dengan huruf Q (tidak disarankan karena menimbulkan kebingungan dengan kuartil).

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung kuintil untuk kumpulan data apa pun.

Kuintil adalah ukuran posisi non-pusat bersama dengan kuartil, desil, dan persentil. Jika Anda lebih tertarik, Anda dapat memeriksa arti dari masing-masing jenis kuantil ini di situs web kami.

Perlu dicatat bahwa kuintil mungkin memiliki definisi lain. Dalam ilmu ekonomi, kuintil mewakili persentase populasi yang diurutkan berdasarkan pendapatan, atau dengan kata lain, mengurutkan populasi berdasarkan tingkat pendapatan. Misalnya, kuintil pertama mewakili 20% penduduk termiskin dalam suatu populasi, kuintil kedua mewakili 40% penduduk dengan pendapatan terendah, dan seterusnya.

Cara menghitung kuintil

Untuk menghitung posisi kuintil suatu sampel atau populasi statistik, Anda harus mengalikan jumlah kuintil dengan jumlah total data ditambah satu dan membagi hasilnya dengan lima.

Oleh karena itu, rumus kuintil adalah:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Harap diperhatikan: hasil rumus ini menunjukkan posisi kuintil, bukan nilainya. Oleh karena itu, kuintilnya adalah data yang terletak pada posisi yang diperoleh rumus.

Namun terkadang hasil rumus ini akan memberikan kita angka desimal, oleh karena itu kita harus membedakan dua kasus tergantung apakah hasilnya berupa angka desimal atau bukan:

Jika hasil rumusnya berupa bilangan tanpa bagian desimal , maka kuintilnya adalah data yang terletak pada posisi yang disediakan rumus di atas.
Jika hasil rumusnya berupa bilangan dengan bagian desimal , nilai kuintil dihitung menggunakan ekspresi berikut:

$K=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

Jika Anda takut ketika melihat begitu banyak langkah untuk menentukan kuintil suatu kumpulan data, jangan khawatir, sebenarnya ini cukup sederhana. Bacalah dua contoh berikut dan Anda pasti akan lebih memahaminya.

Catatan : Komunitas statistik masih belum sepenuhnya sepakat tentang cara penghitungan kuintil, jadi Anda mungkin menemukan buku yang menjelaskannya sedikit berbeda.

Contoh penghitungan kuintil

Di bawah ini kami tinggalkan dua latihan yang diselesaikan langkah demi langkah tentang cara mendapatkan kuintil dari serangkaian data. Jadi, agar Anda dapat melihat dua kemungkinan kasus, pada latihan pertama hasilnya bukan desimal dan pada latihan kedua hasilnya bukan desimal.

Contoh 1

Hitung kuintil dari seri data berikut:

Seperti yang Anda lihat pada penjelasan di atas, rumus mencari posisi kuintil adalah:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Parameter n mengacu pada jumlah data yaitu 49, jadi untuk mencari posisi kuintil pertama kita perlu mengganti n dengan 49 dan k dengan 1:

$\cfrac{1\cdot (49+1)}{5}=10 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_1=205$

Dari rumus tersebut diperoleh angka 10 yang berarti kuintil tersebut berada pada posisi kesepuluh dari daftar berurutan yang sesuai dengan data 205.

Untuk menghitung kuintil kedua, Anda harus menggunakan rumus yang sama tetapi mengganti k dengan 2:

$\cfrac{2\cdot (49+1)}{5}=20 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_2=236$

Oleh karena itu, kuintil kedua berada pada posisi nomor 20 dari daftar terurut, yaitu nilai 236.

Sekali lagi, kita ulangi proses untuk menentukan kuintil 3 tetapi, secara logis, kita sekarang mengganti k dengan 3:

$\cfrac{3\cdot (49+1)}{5}=30 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_3=266$

Jadi, kuintil ketiga adalah data yang terletak pada posisi 30, yang setara dengan 266.

Terakhir, kami menerapkan kembali rumus tersebut untuk menghitung kuintil keempat:

$\cfrac{4\cdot (49+1)}{5}=40 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_4=286$

Oleh karena itu, kuintil keempat berada pada posisi 40, sehingga kuintil keempat adalah 286.

Contoh 2

Hitung empat kuintil data statistik yang dikumpulkan pada tabel berikut :.

Sama seperti contoh sebelumnya, untuk mendapatkan posisi kuintil harus menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Dalam hal ini jumlah sampel adalah 42 observasi, sehingga untuk mencari posisi kuintil pertama kita perlu mengganti parameter n dengan 42 dan k dengan 1:

$\cfrac{1\cdot (42+1)}{5}=8,6$

Namun, berbeda dengan contoh pertama, kali ini rumusnya memberi kita angka desimal, jadi kita perlu menerapkan rumus berikut untuk menghitung kuintil eksak:

$K=x_i+d\cdot (x_{i+1}-x_i)$

Angka yang didapat dari rumus pertama adalah 8,6, jadi kuintil pertama berada di antara data kedelapan dan kesembilan, yaitu masing-masing 78 dan 79. Jadi, x _i adalah 78, x _i+1 adalah 79 dan d adalah bagian desimal dari bilangan yang diperoleh, yaitu 0,6.

$K_1=78+0,6\cdot (79-78)=78,6$

Sekarang kita melakukan prosedur yang sama lagi untuk mencari kuintil kedua. Kita hitung dulu posisinya:

$\cfrac{2\cdot (42+1)}{5}=17,2$

Namun dari rumus tersebut kita memperoleh bilangan desimal antara 17 dan 18 sehingga kuintil kedua berada di antara posisi ketujuh belas dan kedelapan belas, yang nilainya masing-masing sesuai dengan 109 dan 112 dari daftar yang diurutkan. Oleh karena itu, kami menerapkan rumus kedua dalam proses untuk menentukan nilai kuintil yang tepat:

$K_2=109+0,2\cdot (112-109)=109,6$

Kita ulangi cara untuk mendapatkan kuintil ketiga, kita tentukan dulu posisinya:

$\cfrac{3\cdot (42+1)}{5}=25,8$

Angka yang dihitung 25,8 berarti nilai kuintil berada di antara posisi dua puluh lima dan dua puluh enam, yang nilainya 134 dan 141. Oleh karena itu, perhitungan nilai kuintil pastinya adalah:

$K_3=134+0,8\cdot (141-134)=139,6$

Terakhir, kita ulangi prosedur yang sama untuk terakhir kalinya untuk menghitung kuintil 4. Pertama-tama kita cari posisinya:

$\cfrac{4\cdot (42+1)}{5}=34,4$

Oleh karena itu, nilai pasti kuintil keempat adalah antara 34 dan 35, yang posisinya sesuai dengan data 172 dan 179. Oleh karena itu, perhitungan kuintil keempat adalah:

$K_4=172+0,4\cdot (179-172)=174,8$

Kalkulator Kuintil

Masukkan kumpulan data statistik ke dalam kalkulator berikut untuk menghitung kuintil. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Kuintil dalam data yang dikelompokkan

Untuk menghitung kuintil ketika data dikelompokkan ke dalam interval, Anda harus mencari interval atau kelasnya terlebih dahulu menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Oleh karena itu, kuintil akan berada dalam interval yang frekuensi absolutnya lebih besar daripada angka yang diperoleh dengan ekspresi sebelumnya.

Dan setelah kita mengetahui interval yang termasuk dalam kuintil tersebut, kita harus menerapkan rumus berikut untuk mencari nilai pasti dari kuintil tersebut:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4$

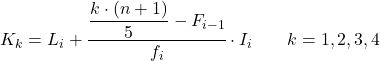
Emas:

L _i adalah batas bawah interval di mana kuintil berada.
n adalah jumlah total pengamatan.
F _i-1 adalah frekuensi absolut kumulatif dari interval sebelumnya.
f _i adalah frekuensi absolut dari interval di mana kuintil berada.
I _i adalah lebar interval kuintil.

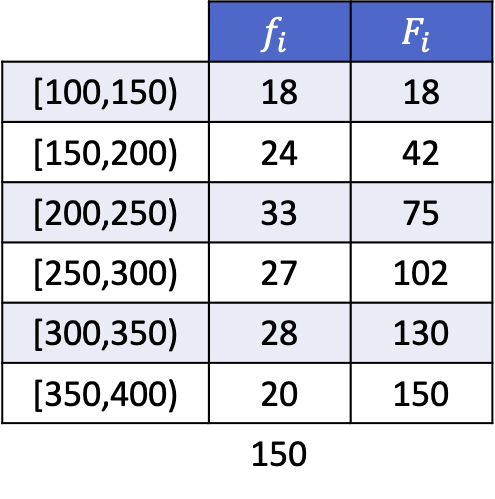
Agar Anda dapat melihat cara melakukannya, berikut adalah contoh penyelesaian penghitungan kuintil dari rangkaian data berikut yang dikelompokkan ke dalam interval:

kumpulan data yang dikelompokkan ke dalam interval

Karena datanya dikelompokkan, kita harus menggunakan metode berikut untuk menghitung kuintil: pertama-tama tentukan rentang kuintil tersebut, lalu cari nilai pasti dari kuintil tersebut.

Jadi, untuk mencari interval letak kuintil pertama, kita menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{5}$

$\cfrac{1\cdot (150+1)}{5} =30,2 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [150,200)$

Kuintil pertama akan berada pada interval yang frekuensi absolut kumulatifnya langsung lebih besar dari 30,2, dalam hal ini adalah interval [150,200) yang frekuensi absolut kumulatifnya adalah 42. Dan setelah kita mengetahui interval kuintilnya, kita terapkan rumus kedua dari persamaan tersebut. proses untuk menentukan nilai pastinya:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i$

$K_1=150+\cfrac{\displaystyle\frac{1\cdot (150+1)}{5}-18}{24}\cdot 50=175,42$

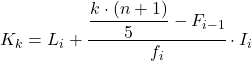
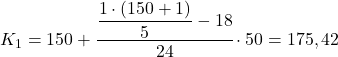
Sekarang kita ulangi prosedur yang sama untuk mendapatkan kuintil kedua, pertama-tama hitung interval letaknya:

$\cfrac{2\cdot (150+1)}{5} =60,4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [200,250)$

Frekuensi absolut kumulatif tepat di atas 60,4 adalah 75, sehingga rentang kuintil kedua adalah [200.250). Oleh karena itu, kami mengganti nilai yang sesuai ke dalam rumus kedua untuk menghitung nilai kuintil yang tepat:

$K_2=200+\cfrac{\displaystyle\frac{2\cdot (150+1)}{5}-42}{33}\cdot 50=227,88$

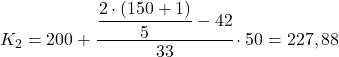
Prosedur yang sama kita lakukan untuk ketiga kalinya untuk mendapatkan kuintil 3. Kita tentukan terlebih dahulu interval letak kuintil tersebut:

$\cfrac{3\cdot (150+1)}{5} =90,6 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [250,300)$

Kuintilnya berada pada interval [250.300) karena frekuensi absolut kumulatifnya (102) berada tepat di atas 90,6. Maka perhitungan nilai eksak kuintil ketiga adalah sebagai berikut:

$K_3=250+\cfrac{\displaystyle\frac{3\cdot (150+1)}{5}-75}{27}\cdot 50=278,89$

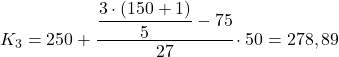
Terakhir, kita akan menemukan kuintil keempat. Seperti biasa, pertama-tama kita cari intervalnya:

$\cfrac{4\cdot (150+1)}{5} =120,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [300,350)$

Interval yang frekuensi absolutnya lebih besar dari 120,8 adalah [300,350), yang nilainya 130. Oleh karena itu, nilai pasti kuintil keempat adalah:

$K_4=300+\cfrac{\displaystyle\frac{4\cdot (150+1)}{5}-102}{28}\cdot 50=333,57$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa itu kuintil?

Cara menghitung kuintil

Contoh penghitungan kuintil

Contoh 1

Contoh 2

Kalkulator Kuintil

Kuintil dalam data yang dikelompokkan

Tentang Penulis

Benjamin anderson

Tambahkan komentar