Cara melakukan tes kurangnya kesesuaian di r (langkah demi langkah)
Uji kekurangan kecocokan digunakan untuk menentukan apakah model regresi penuh memberikan kesesuaian yang jauh lebih baik terhadap kumpulan data dibandingkan dengan versi model yang diperkecil.
Misalnya, kita ingin menggunakan jumlah jam belajar untuk memprediksi nilai ujian siswa di perguruan tinggi tertentu. Kita dapat memutuskan untuk mengadaptasi dua model regresi berikut:
Model lengkap: skor = β 0 + B 1 (jam) + B 2 (jam) 2
Model tereduksi: skor = β 0 + B 1 (jam)
Contoh langkah demi langkah berikut menunjukkan cara melakukan uji kekurangan kecocokan di R untuk menentukan apakah model penuh memberikan kesesuaian yang jauh lebih baik daripada model tereduksi.
Langkah 1: Buat dan visualisasikan kumpulan data
Pertama, kita akan menggunakan kode berikut untuk membuat kumpulan data yang berisi jumlah jam belajar dan nilai ujian yang diperoleh untuk 50 siswa:
#make this example reproducible set. seeds (1) #create dataset df <- data. frame (hours = runif (50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2) #view first six rows of data head(df) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
Selanjutnya, kita akan membuat diagram sebar untuk memvisualisasikan hubungan antara jam dan skor:
#load ggplot2 visualization package library (ggplot2) #create scatterplot ggplot(df, aes (x=hours, y=score)) + geom_point()
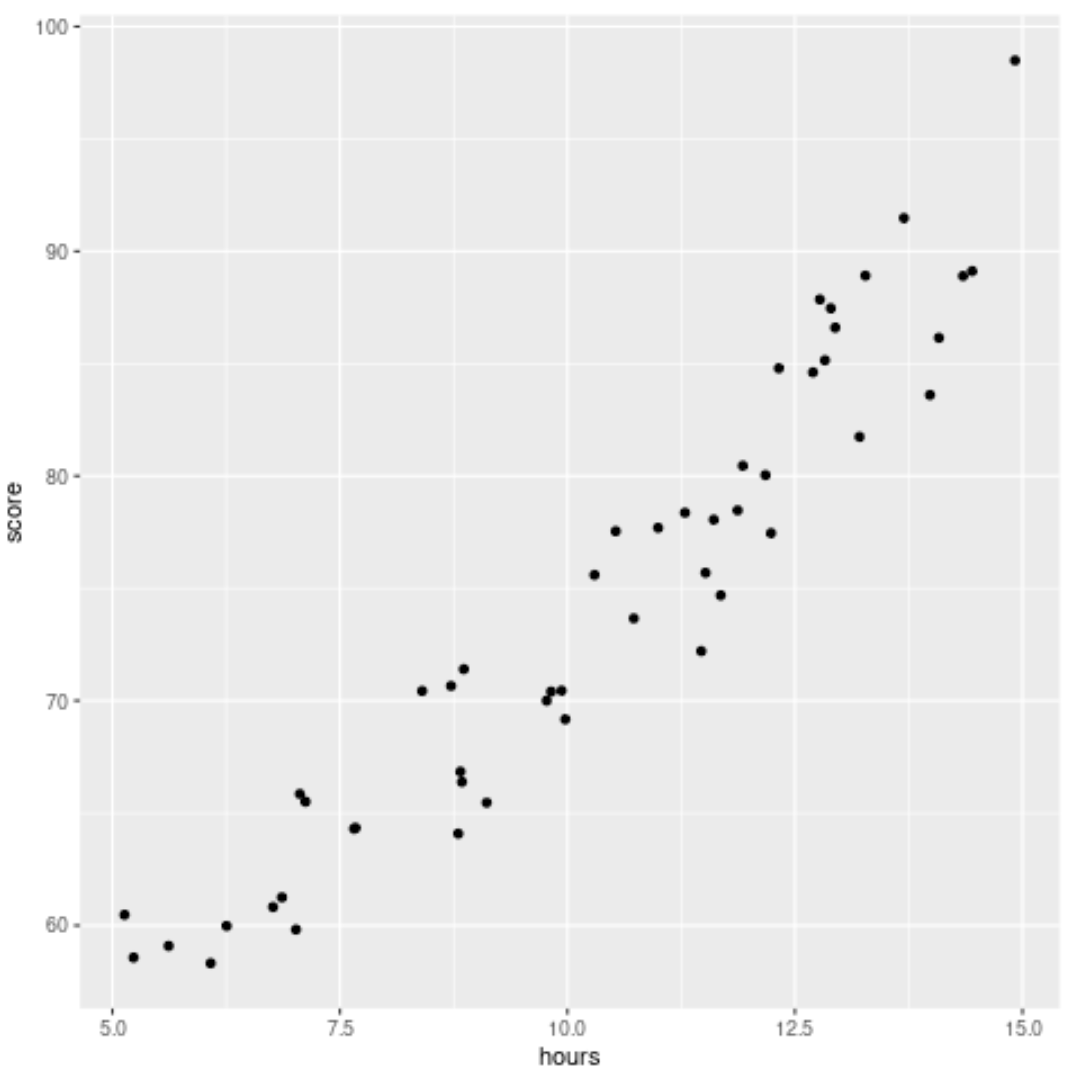
Langkah 2: Sesuaikan dua model berbeda ke kumpulan data
Selanjutnya, kita akan memasukkan dua model regresi berbeda ke kumpulan data:
#fit full model full <- lm(score ~ poly (hours,2), data=df) #fit reduced model reduced <- lm(score ~ hours, data=df)
Langkah 3: Lakukan uji kekurangan kecocokan
Selanjutnya, kita akan menggunakan perintah anova() untuk melakukan uji kekurangan kecocokan antara kedua model:
#lack of fit test
anova(full, reduced)
Analysis of Variance Table
Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 368.48
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Statistik uji F ternyata 10,554 dan nilai p yang sesuai adalah 0,002144 . Karena nilai p ini kurang dari 0,05, kita dapat menolak hipotesis nol dari pengujian tersebut dan menyimpulkan bahwa model lengkap secara statistik memberikan kesesuaian yang jauh lebih baik daripada model tereduksi.
Langkah 4: Visualisasikan model akhir
Terakhir, kita dapat memvisualisasikan model akhir (model lengkap) terhadap kumpulan data asli:
ggplot(df, aes (x=hours, y=score)) +
geom_point() +
stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) +
xlab(' Hours Studied ') +
ylab(' Score ')
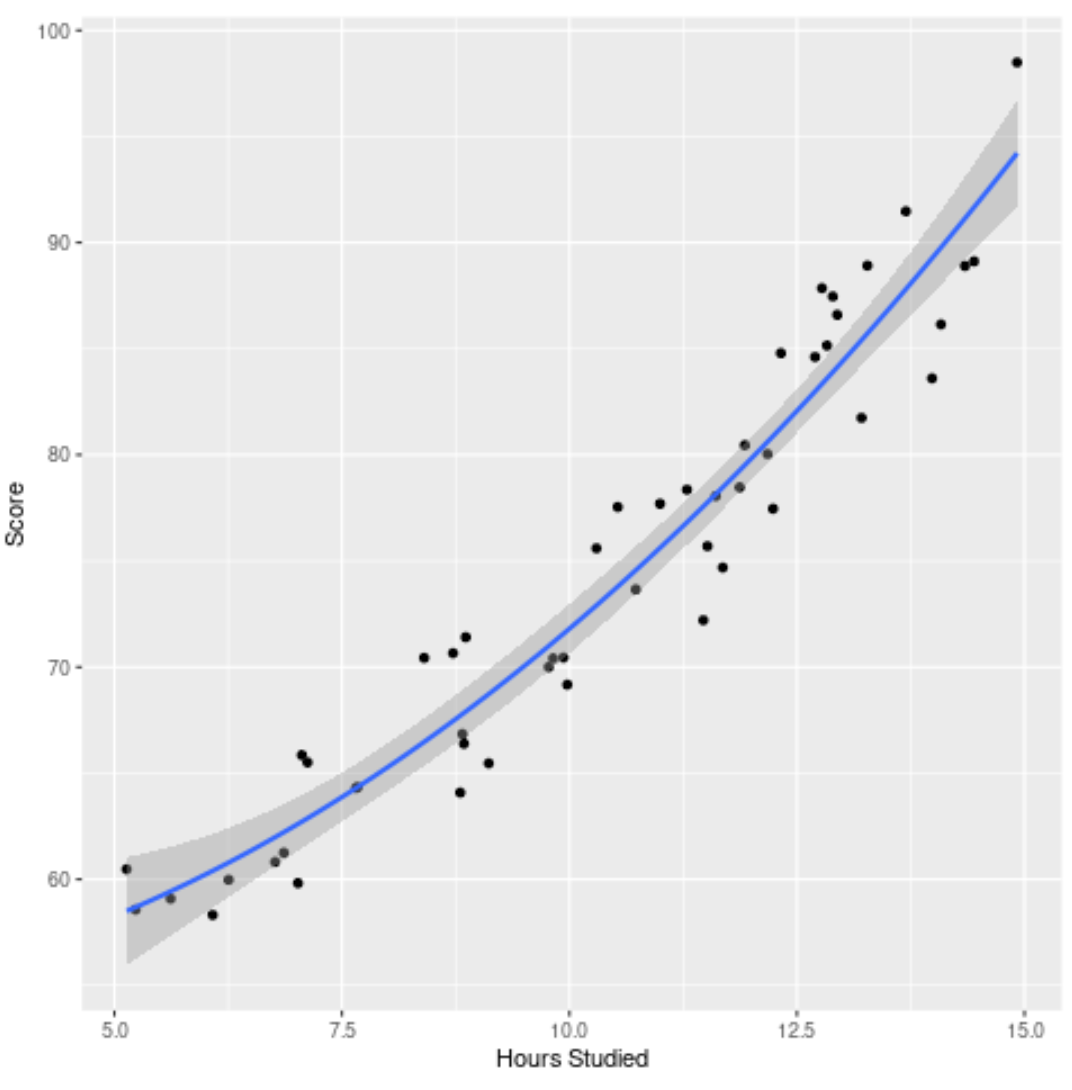
Kita dapat melihat bahwa kurva model cukup sesuai dengan data.
Sumber daya tambahan
Cara melakukan regresi linier sederhana di R
Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi polinomial di R