Cara membuat dan menafsirkan kurva roc di spss

Regresi logistik adalah metode statistik yang kami gunakan untuk menyesuaikan model regresi jika variabel responsnya biner. Untuk mengevaluasi seberapa cocok model regresi logistik dengan kumpulan data, kita dapat melihat dua metrik berikut:

• Sensitivitas: probabilitas model memprediksi hasil positif untuk suatu observasi padahal hasilnya benar-benar positif.
• Kekhususan: probabilitas model memprediksi hasil negatif untuk suatu observasi padahal hasilnya sebenarnya negatif.

Cara sederhana untuk memvisualisasikan kedua metrik ini adalah dengan membuat kurva ROC , yaitu grafik yang menampilkan sensitivitas dan spesifisitas model regresi logistik.

Tutorial ini menjelaskan cara membuat dan menginterpretasikan kurva ROC di SPSS.

Contoh: Kurva ROC di SPSS

Katakanlah kita memiliki kumpulan data berikut yang menunjukkan apakah seorang pemain bola basket direkrut ke NBA atau tidak (0 = tidak, 1 = ya) serta rata-rata poin per permainannya di perguruan tinggi:

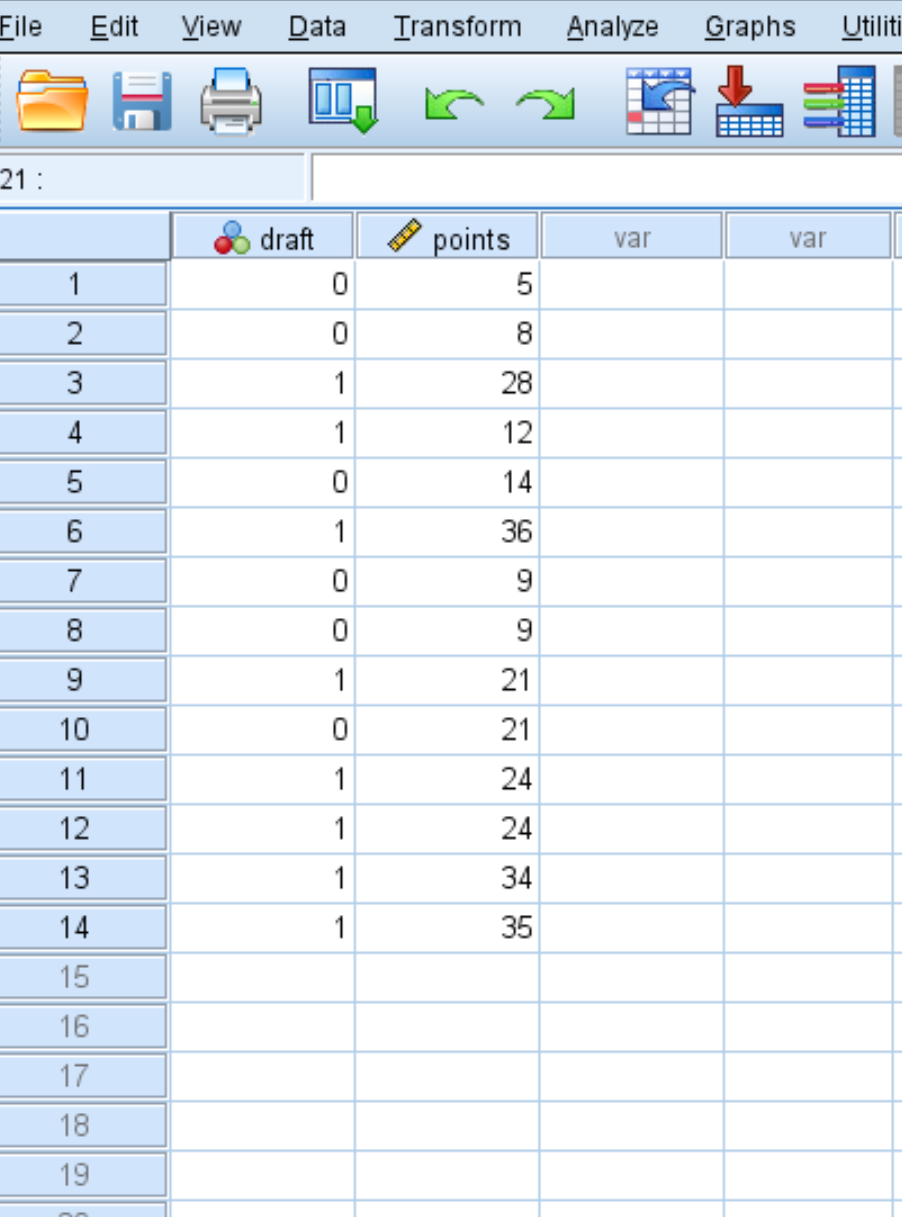
Untuk membuat kurva ROC untuk kumpulan data ini, klik tab Analisis , lalu Klasifikasikan , lalu Kurva ROC :

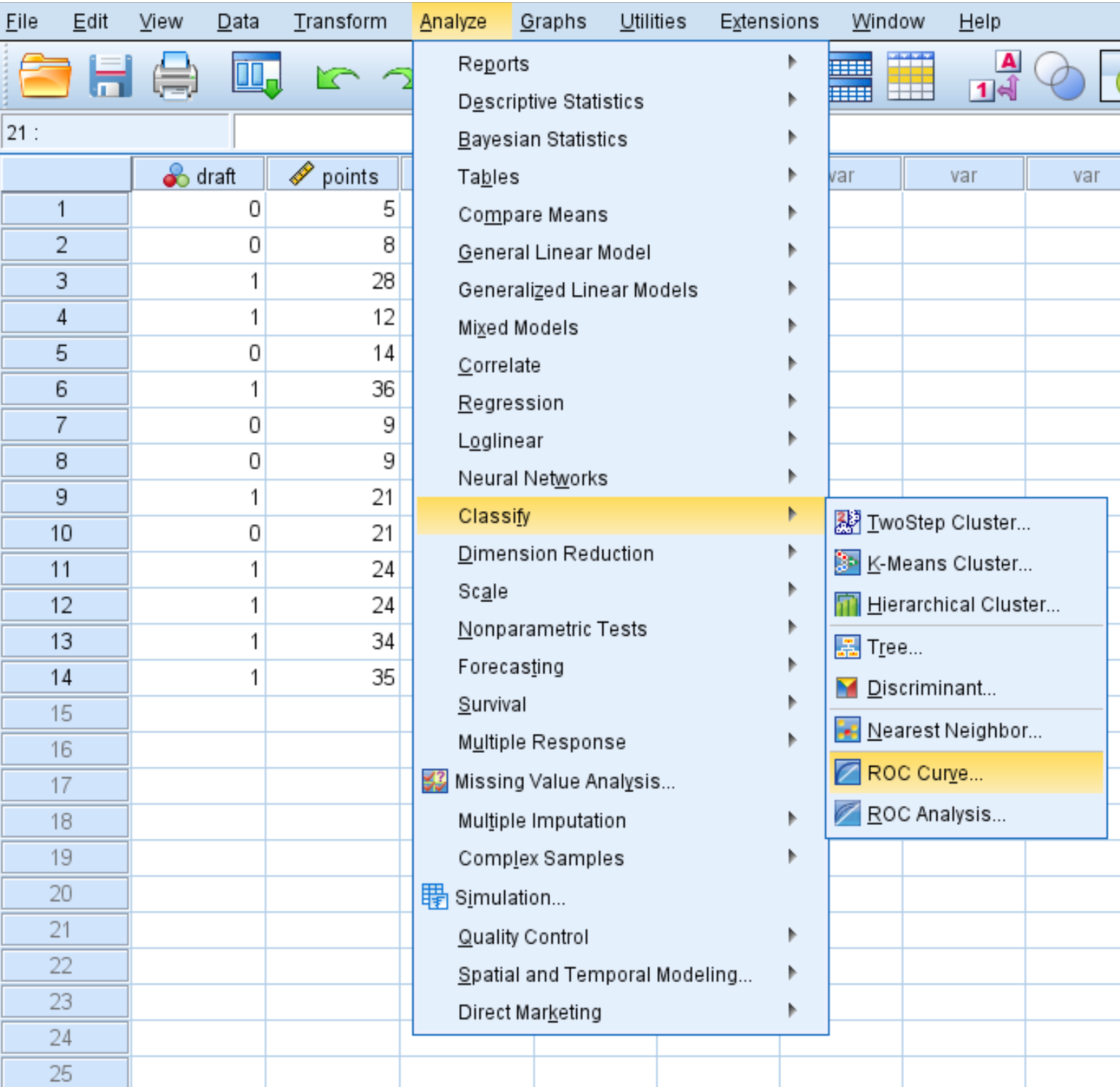
Di jendela baru yang muncul, seret variabel draf ke dalam area berlabel Variabel Status. Tetapkan nilai variabel status menjadi 1 . (Ini adalah nilai yang menunjukkan seorang pemain telah direkrut). Seret titik variabel ke dalam area berlabel Variabel Uji.

Centang kotak di samping Dengan garis referensi diagonal dan koordinat titik kurva ROC . Lalu klik oke .

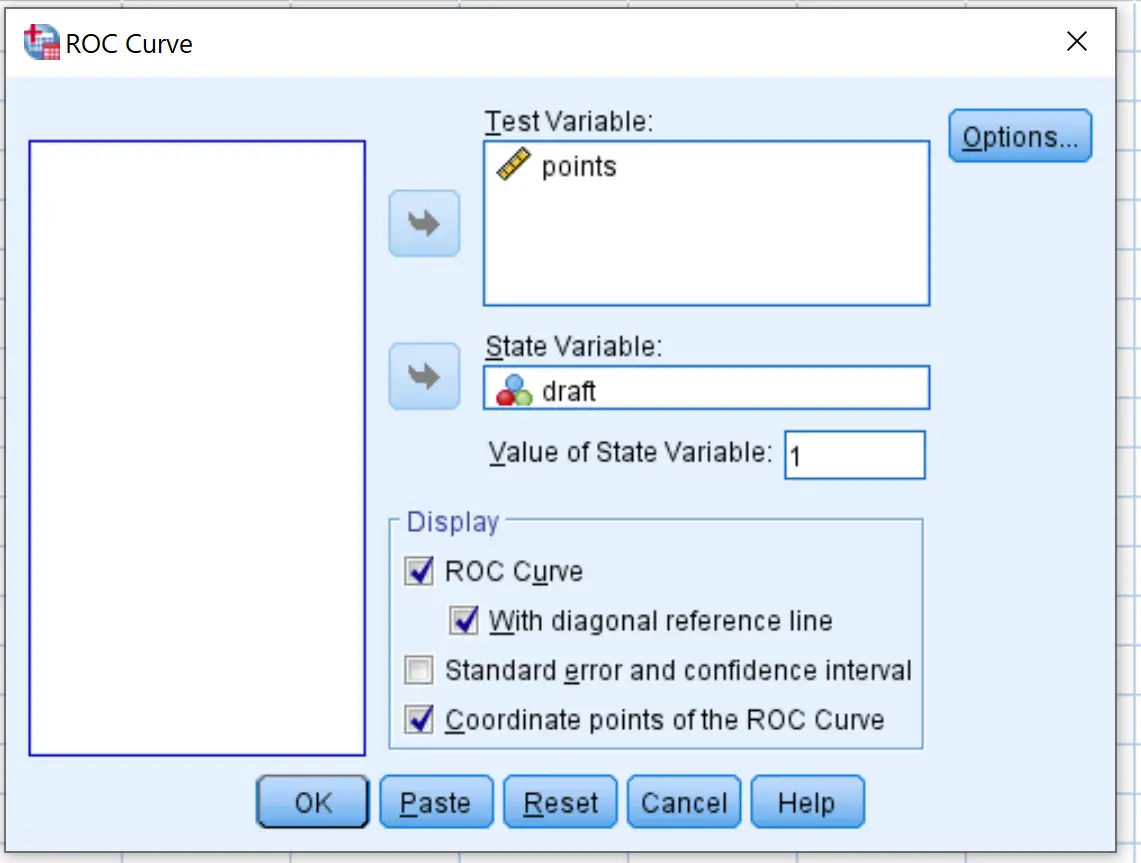
Berikut cara menafsirkan hasilnya:

Ringkasan pemrosesan file:

Tabel ini menampilkan jumlah kasus positif dan negatif dalam dataset. Dalam contoh ini, 8 pemain direkrut (hasil positif) dan 6 pemain tidak direkrut (hasil negatif):

Kurva ROC:

Kurva Receiver Operating Characteristic (ROC) merupakan plot nilai sensitivitas versus spesifisitas 1 seiring perubahan nilai ambang batas dari 0 menjadi 1:

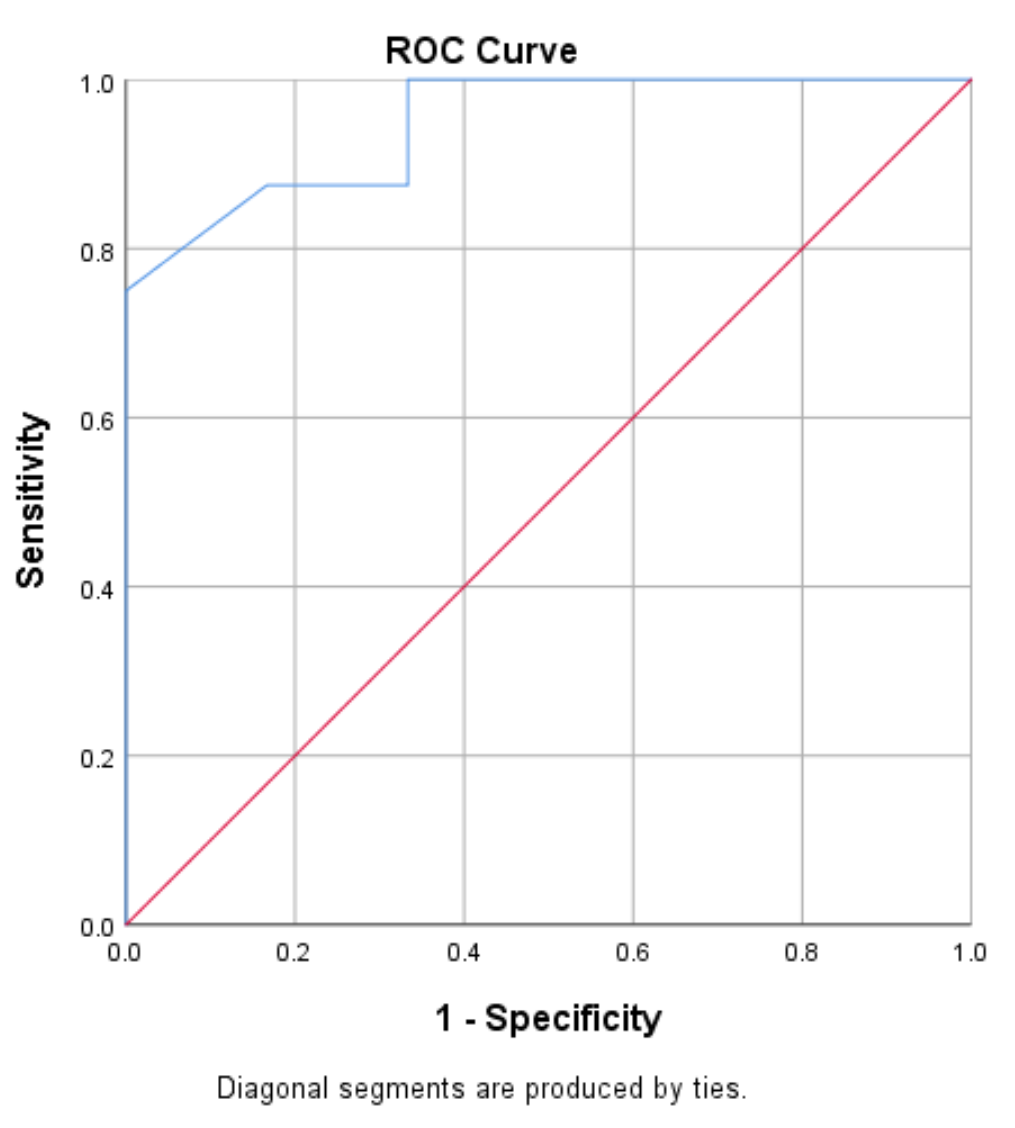
Model dengan sensitivitas dan spesifisitas tinggi akan memiliki kurva ROC yang sesuai dengan sudut kiri atas plot. Model dengan sensitivitas dan spesifisitas rendah akan memiliki kurva mendekati diagonal 45 derajat.

Kita dapat melihat bahwa kurva ROC (garis biru) dalam contoh ini berada di sudut kiri atas plot, yang menunjukkan bahwa model tersebut berhasil memprediksi pemain apakah akan direkrut atau tidak, berdasarkan poin rata-rata mereka per game. . .

Area di bawah kurva:

Area di bawah kurva memberi kita gambaran tentang kemampuan model dalam membedakan hasil positif dan negatif. AUC dapat berkisar dari 0 hingga 1. Semakin tinggi AUC, semakin baik model dalam mengklasifikasikan hasil dengan benar.

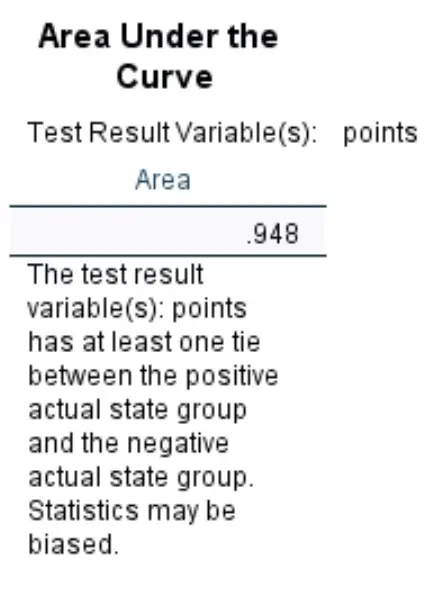
Kita dapat melihat bahwa AUC untuk model regresi logistik khusus ini adalah 0,948 , yang merupakan angka yang sangat tinggi. Hal ini menunjukkan bahwa model tersebut mampu memprediksi dengan baik apakah seorang pemain akan direkrut atau tidak.

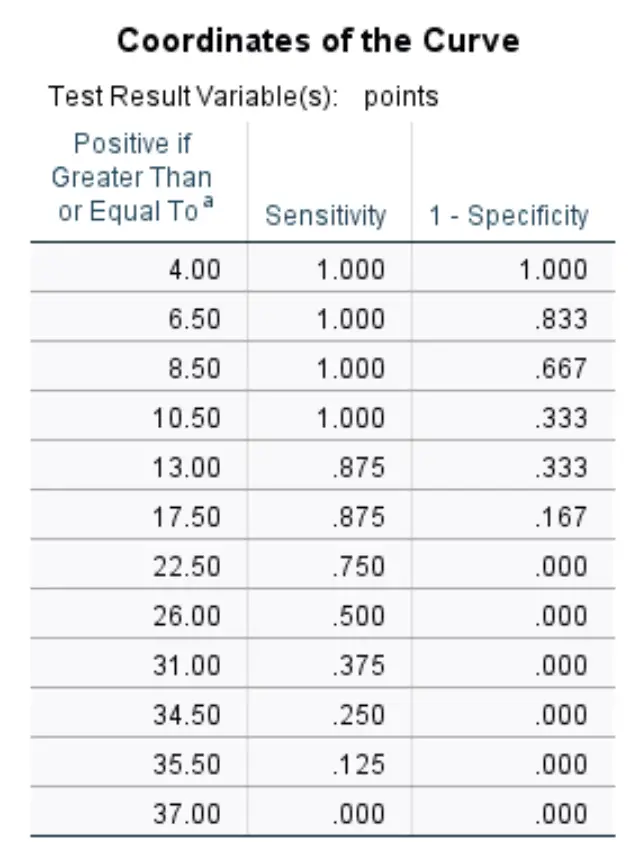
Koordinat kurva:

Tabel terakhir ini menampilkan sensitivitas dan spesifisitas 1 kurva ROC untuk ambang batas yang berbeda.

Misalnya:

Jika kami mengizinkan ambang batas menjadi 8,50 , ini berarti kami memperkirakan bahwa setiap pemain yang mencetak kurang dari 8,50 poin per game tidak akan direkrut, dan setiap pemain yang mencetak lebih dari 8,50 poin per game akan direkrut.

Menggunakan ini sebagai ambang batas, sensitivitas kami akan menjadi 100% (karena setiap pemain yang mencetak kurang dari 8,50 poin per game memang tidak direkrut) dan spesifisitas kami 1 akan menjadi 66,7% (karena 8 pemain dari 12 yang mencetak lebih dari 8,50 poin per game dirancang).

Tabel di atas memungkinkan kita melihat sensitivitas dan spesifisitas 1 untuk setiap ambang batas potensial.