Kurva lorenz
Artikel ini menjelaskan apa itu kurva Lorenz dan kegunaannya. Anda akan menemukan cara membuat kurva Lorenz suatu populasi dan, sebagai tambahan, Anda akan dapat melihat penyelesaian latihan langkah demi langkah. Terakhir, disajikan sifat-sifat kurva Lorenz dan hubungannya dengan indeks Gini.
Apa yang dimaksud dengan kurva Lorenz?
Kurva Lorenz merupakan representasi grafis dari kesenjangan ekonomi penduduk suatu wilayah. Dengan kata lain, kurva Lorenz merupakan kurva yang memungkinkan kita menganalisis kesenjangan distribusi pendapatan di suatu wilayah.
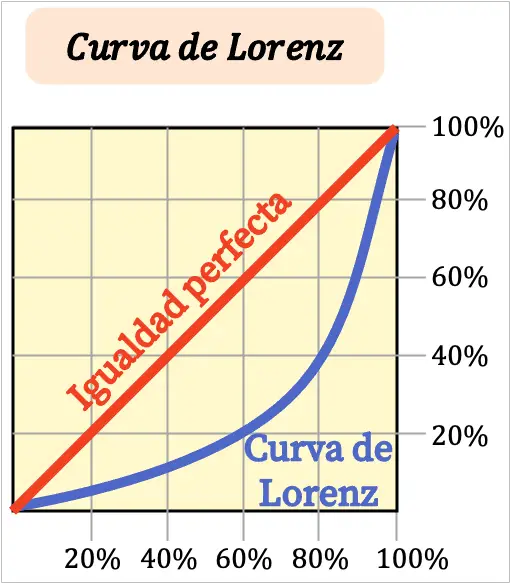
Semakin lurus kurva Lorenz, semakin egaliter pendapatan wilayah tersebut. Sebaliknya, semakin melengkung kurva Lorenz, maka semakin tidak merata distribusi pendapatan.
Biasanya, sumbu kurva Lorenz dinyatakan dalam persentase. Sumbu X pada grafik mewakili persentase jumlah penduduk dan sebaliknya sumbu Y menunjukkan persentase pendapatan.
Kurva Lorenz ditemukan pada tahun 1905 oleh Max Otto Lorenz, seorang ekonom Amerika yang sangat penting pada abad ke-20.
Cara menghitung kurva Lorenz
Setelah kita mengetahui definisi kurva Lorenz, selanjutnya kita akan melihat bagaimana kurva statistik ini dihitung. Perlu dicatat bahwa ada rumus untuk mendefinisikan kurva Lorenz, tetapi dalam praktiknya rumus tersebut umumnya tidak digunakan. Itu sebabnya kami akan menyelesaikan contoh langkah demi langkah sehingga Anda dapat melihat cara melakukannya.
- Kurva Lorenz mewakili penduduk yang pendapatannya disajikan pada tabel berikut:
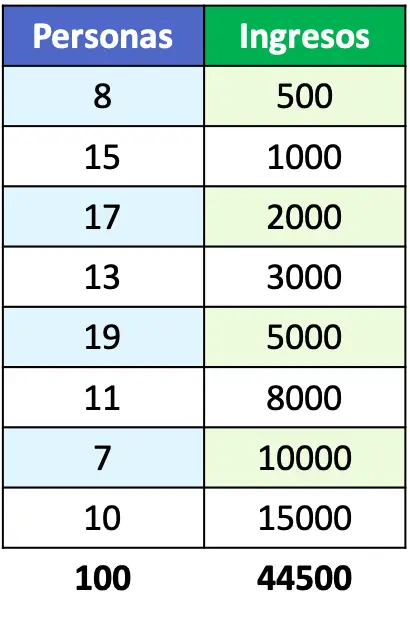
Jika rumusan masalah memberi kita contoh fungsi kurva Lorenz, kita dapat langsung merepresentasikan fungsi tersebut dalam grafik. Namun dalam hal ini mereka hanya memberikan kita pendapatan penduduk, jadi kita harus menghitung persentase tiap kelompok masyarakat.
Jadi, untuk menentukan persentase jumlah penduduk dan pendapatan, kita harus menambahkan dua kolom pada tabel untuk variabel jumlah penduduk:
- Kolom dengan akumulasi frekuensi absolut (F i ).
- Kolom kedua yang sesuai dengan persentase kumulatif, yang dihitung dengan membagi frekuensi absolut kumulatif dengan jumlah total orang.
Dan sebaliknya, kita harus menambahkan tiga kolom untuk variabel pendapatan:
- Kolom yang menghitung jumlah pendapatan yang setara dengan hasil kali jumlah orang dengan pendapatan yang diterima setiap orang.
- Sedetik dengan akumulasi frekuensi absolut (F i ) dari total pendapatan.
- Kolom ketiga yang memuat persentase akumulasi, ditentukan dengan membagi kolom sebelumnya dengan total pendapatan penduduk.
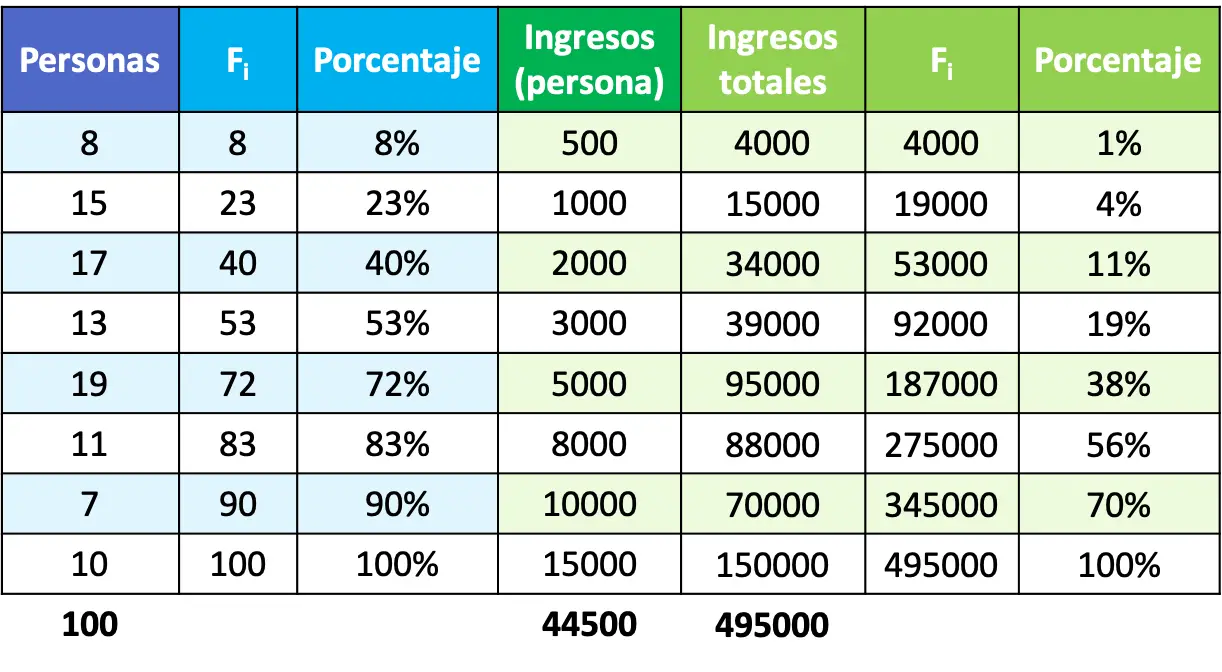
Terakhir, setelah kita menghitung persentasenya, yang tersisa hanyalah memplot titik-titik tersebut pada grafik dan menggabungkannya untuk membentuk kurva Lorenz. Ingatlah bahwa sumbu X adalah persentase jumlah penduduk dan sumbu Y adalah persentase pendapatan.
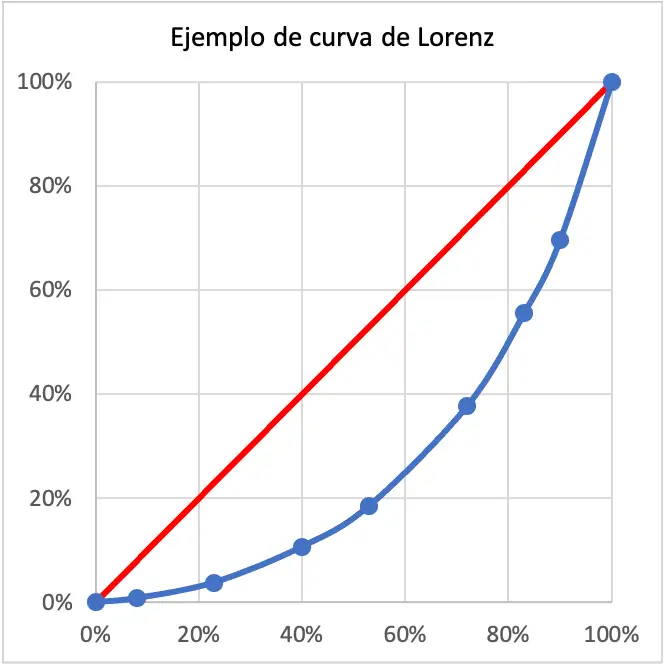
Dalam hal ini pendapatan penduduk yang diteliti sangat timpang karena kurva Lorenz sangat lebar. Faktanya, kurva Lorenz sangat jauh dari garis merah yang melambangkan pemerataan sempurna.
Interpretasi kurva Lorenz
Bagian ini menjelaskan cara menafsirkan kurva Lorenz suatu populasi, karena selain mengetahui cara membuat grafiknya, Anda juga perlu memahami maksudnya.
Kurva Lorenz menunjukkan berapa persentase penduduk yang memiliki persentase pendapatan total suatu wilayah. Misalnya pada contoh kurva Lorenz di atas, 40% penduduk mempunyai pendapatan sebesar 11% dari seluruh pendapatan penduduk. Jadi wilayahnya sangat tidak merata.
Dengan demikian, kurva Lorenz secara visual merepresentasikan persamaan atau ketimpangan pendapatan antar penduduk suatu negara atau wilayah. Semakin jauh kita menjauh dari garis yang menunjukkan kesetaraan sempurna, hal ini berarti semakin tidak meratanya pendapatan penduduk. Sebaliknya, semakin dekat kurva Lorenz ke kanan, berarti semakin merata distribusi pendapatan penduduk.
Selain itu, jika satu kurva Lorenz berada di atas kurva Lorenz lainnya di sepanjang grafik, ini berarti pendapatan penduduk pertama lebih setara dibandingkan pendapatan penduduk kedua.
Kurva Lorenz dan koefisien Gini
Sebagaimana dijelaskan di seluruh artikel, kurva Lorenz secara grafis menunjukkan bagaimana pendapatan suatu wilayah didistribusikan dan seberapa tidak meratanya suatu wilayah.
Di sisi lain, koefisien Gini, disebut juga indeks Gini, secara numerik menunjukkan ketimpangan ekonomi suatu wilayah.
Oleh karena itu, kurva Lorenz dan koefisien Gini saling terkait. Memang benar, koefisien Gini suatu negara dapat dihitung dari kurva Lorenz-nya. Di artikel berikut Anda dapat melihat cara melakukannya:
Sifat-sifat kurva Lorenz
Kurva Lorenz memiliki sifat sebagai berikut:
- Kurva Lorenz selalu dimulai pada titik (0,0) dan berakhir pada (100,100).
- Kurva Lorenz tidak terdefinisi jika mean sampelnya nol.
- Kurva Lorenz tidak dapat muncul pada grafik di atas garis persamaan sempurna.
- Dengan asumsi pendapatan tidak boleh negatif, kurva Lorenz selalu meningkat.