Maksudnya populasi

Oleh Benjamin anderson Agustus 3, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa arti populasi dalam statistik. Demikian pula, Anda akan mengetahui apa rumus rata-rata populasi, bagaimana interval kepercayaan rata-rata populasi dihitung, dan selanjutnya, apa perbedaan antara rata-rata populasi dan rata-rata sampel.

Berapa rata-rata populasinya?

Rata-rata populasi adalah rata-rata aritmatika dari seluruh elemen populasi statistik. Oleh karena itu, untuk menghitung mean populasi, semua nilai populasi harus dijumlahkan kemudian dibagi dengan jumlah seluruh elemen dalam populasi.

Simbol mean populasi adalah huruf Yunani μ.

Demikian pula, mean populasi juga dapat didefinisikan sebagai nilai yang diharapkan dari variabel yang mewakili suatu populasi.

Cara menghitung rata-rata populasi

Setelah kita melihat definisi mean populasi, mari kita lihat bagaimana mean populasi dihitung untuk lebih memahami maknanya.

Jika semua nilai dalam populasi statistik diketahui, rumus mean aritmatika sebaiknya diterapkan untuk menghitung mean populasi. Jadi dalam hal ini, untuk menghitung mean populasi, kita perlu menjumlahkan semua nilai populasi lalu membaginya dengan jumlah total data.

Jadi, jika kita mengetahui nilai seluruh elemen populasi, maka rumus menghitung mean populasi adalah sebagai berikut:

$\displaystyle\mu=\frac{\displaystyle \sum_{i=1}^N x_i}{N}=\frac{x_1+x_2+\dots +x_N}{N}$

➤ Lihat: Contoh penghitungan mean aritmatika

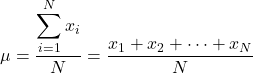
Namun pada umumnya tidak semua nilai populasi diketahui, sehingga biasanya nilai mean populasi diperkirakan dengan interval .

Interval kepercayaan untuk rata-rata populasi

Dalam praktiknya, tidak mungkin mempelajari semua individu dalam suatu populasi, sehingga sampel acak dari populasi biasanya dipilih dan, berdasarkan nilainya, dilakukan perkiraan nilai rata-rata populasi. Lebih tepatnya, kita menghitung interval di mana kemungkinan besar rata-rata seluruh populasi berada; interval ini disebut interval kepercayaan untuk mean populasi.

Interval kepercayaan mean populasi dihitung dengan menjumlahkan dan mengurangkan nilai Z _α/2 dari mean sampel dikalikan simpangan baku (σ) dan dibagi dengan akar kuadrat tinggi sampel (n). Oleh karena itu, rumus menghitung selang kepercayaan mean populasi adalah:

$\displaystyle \left(\overline{x}-z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \ , \ \overline{x}+z_{\alpha/2}\cdot \frac{\sigma}{\sqrt{n}} \right)$

Rumus di atas digunakan bila varians populasi diketahui. Namun, jika varians populasi tidak diketahui, yang merupakan kasus paling umum, interval kepercayaan untuk mean dihitung menggunakan rumus berikut:

$\displaystyle \left(\overline{x}-t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \ , \ \overline{x}+t_{\alpha/2}\cdot \frac{s}{\sqrt{n}} \right)$

Emas:

$\overline{x}$

adalah sarana sampel.
$t_{\alpha/2}$

adalah nilai distribusi t Student n-1 derajat kebebasan dengan probabilitas α/2. Untuk ukuran sampel besar dan tingkat kepercayaan 95% biasanya mendekati 1,96 dan untuk tingkat kepercayaan 99% biasanya mendekati 2,576.
$s$

adalah deviasi standar sampel.
$n$

adalah ukuran sampel.

➤ Lihat: Contoh penghitungan selang kepercayaan untuk mean populasi

Rata-rata populasi dan rata-rata sampel

Terakhir, secara ringkas, kita akan meninjau perbedaan antara mean populasi dan mean sampel sehingga kedua konsep statistik ini menjadi jelas.

Perbedaan antara mean populasi dan mean sampel adalah rentang nilai di mana mean dihitung. Rata-rata populasi adalah rata-rata dari seluruh populasi statistik, sedangkan rata-rata sampel adalah rata-rata sampel dari populasi.

Selain itu, untuk membedakan mean populasi dari mean sampel, keduanya diwakili oleh simbol yang berbeda. Yang dimaksud dengan lambang penduduk adalah

$\mu$

, sebaliknya, simbol untuk mean sampel adalah

$\overline{x}$

$\begin{array}{c}\mu =\text{Media poblacional}\\[2ex]\overline{x} = \text{Media muestral}\end{array}$

Jika Anda masih ragu dengan perbedaan kedua jenis rata-rata ini atau ingin mengetahui lebih jauh tentang cara menghitung rata-rata sampel, Anda dapat membaca artikel berikut ini:

➤ Lihat: Apa arti sampelnya?

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya